Astrophysics S1

what is sensitivity of astronomical observations determined by

sign-to-noise ratio (SNR)

signal of source (S)

# of photons collected in a given exposure time

noise level (N)

uncertainty in photon count (N = sqrt(S))

SNR

SNR = S / N = sqrt(S)

what is SNR proportional to

sqrt(F) sqrt(t_exp) D

F = flux

t_exp= exposure time

D = diameter of telescope

Spectral resolution

R = λ/Δλ

the minimum spectral width that can be measured (Δλ) at some wavelength (λ)

[just a ratio!!]

spatial resolution

smallest size of source/feature that can be measured in an image at some wavelength λ

diffraction limited imaging

telescopes in space

θ = λ_mirror / D_mirror

seeing limited imaging

θ = 1.22λ / r₀ (r₀ ~ 10-30cm, Fried’s coherence length)

single telescope on earth

interferometery

θ = 1.22λ / D_baseline (D_baseline = maximum possible distance between any two telescopes)

multiple telescopes on earth

light wave equations

c = vλ

E = hv

energy with flux F passing through area dA in time dt

E = FdAdt

luminosity for spherically steady source

L = 4πr² F(r)

Flux of a spherically steady object, in terms of its radius

F(r) = L / 4πr²

note about L and F

L is integrated over all wavelengths but real detectors are sensitive to certain values. SO, consider incident radiation distribution over frequency. F = ∫ F_v (v) dv where F_v is flux density

black body radiation

source in thermodynamic equilibrium with surroundings and emits as a black body (opaque and non reflective)

Wien Displacement Law

λ_max = 2.9e-3 / T

hv_max = 2.8k_BT

[for temperature of a black body]

Stefan-Boltzman Law

F = σT⁴

therefore L = 4πR²σT⁴

[for flux and luminosity of a black body]

Luminosity of a black body

L / L₀ = (R / R₀)² (T / T₀)⁴

Intensity of a blackbody at temperature T

(Planck Function)

B_v(T) = (2hv³ / c²) / (exp(hv / kT) - 1)

B_λ(T) = (2hc² / λ⁵) / (exp(hc / λkT) - 1)

Rayleigh-Jean

hv << kT

B_v ~ 2v² kT / c²

Wien Law

hv >> kT

B_v ~ (2hv³ / c²) exp(-hv/kt)

Synchotron Radiation

charge particle accelerated in spiral path around magnetic field line, leading to photon emission over a continuous power law spectrum: P(v) ∝ v^-8

e.g. radio galaxies, supernovae remnants

Brehmstrahlung Radiation

‘breaking radiation’: charged particle accelerated due to Coulomb force, leading to photon emission (largely in high temperature thermal plasmas where spectrum is continuous i.e. no spectral lines)

P(v, t) ∝ exp(-hv / kT)

e.g. in ionised gas clusters in galaxies

Spectral lines (bound-bound)

electrons make transitions between different states, leading to photon emission. hv = | E_initial - E_final |

emission lines

from optically thin volume of gas with no background light

absorption lines

cold gas in front of higher temperature source

finite width of spectral lines is given by

ΔEΔt = h/2 → natural linewidth

collisional broadening Δv ∝ collisions per second ∝ density

doppler broadening: resulting from particles with M-B velocity distribution on small scales

doppler effect

spectral lines not always measured at rest wavelength (λ_rest). this difference can be used to detect exoplanets, weighing galaxies/clusters etc.

doppler effect (non relativistic)

λ_obs = λ_rest [1 + v/c]

therefore: Δλ / λ = v / c because Δλ = λ_obs - λ_rest

doppler effect (relativistic)

λ_obs = λ_rest [(1 + v/c) / (1 - v/c)]^½

red shift

z = Δλ / λ

circular velocity

velocity of an object undergoing uniform circular motion:

v_circ = sqrt( GM / r )

escape velocity

minimum velocity needed for an object at distance r to escape gravitational interference of a body with mass M. (equate gravitational potential energy to kinetic energy)

v_esc = sqrt( 2GM / r )

solar system

terrestrial planets, giant (jovian) planets, small bodies e.g. comets …

comets

• primordial remains of early solar system

• mostly ice and dust

• eccentric oribits

• in Kuiper belt (>30 Au) or Oort Cloud (3000 - 10,000 Au)

asteroids

• minor planets of size ~ 30m - 1000 km

• locked in resonant orbits of main planets e.g. jupiter due to gravitational influence

• in asteroid belt between mars and jupiter

Kepler I

each planet moves in an ellipse with the sun at one focus

Kepler II

line connecting a planet and its sun sweeps out equal areas in equal times

Kepler III

For all planets:

square of orbital period ∝ cube of semi-major axis

P² = ka³

periapsis

closest point to star at the focus F

apoapsis

furthest point from star at F

formation of planets

proto-planetary disks have particles that collide and stick together through electrostatic forces (they dissipate KE upon contact). They later become large enough for their gravity to attract other bodies

dust (microns) → pebbles(cm) → planetesimals (km) → planets (1000 km)

distribution of rocky planets / gas giants

because of temperature gradient in protoplanetary disk. surface density of planetesimals was larger beyond the snow line which led to quick formation of planets which grow very quickly to large sizes. The sun heats up and gas in blown outwards and there isn’t enough left for slow-forming rocky planets to capture

snow line

distance from star/sun at which protoplanetary disk has temperature T = 273K

shape of orbits

all orbits are circular if the shape of the protoplanetary disk was circular

finding central pressure

• hydrostatic equilibrium dP/dr = -ρ(r)(GM / r²) (planetary atmospheres, interiors, stars etc.)

• M = 4/3 π R³ <ρ>

• assume density is constant and surface pressure = 0

• ∫dP (P_c to 0) = -<ρ>² (4/3) π G ∫ r dr (0 to R)

• which = 1.4e-10 <ρ>² R²

how to measure temperature of planets

estimate it by assuming absorbed solar energy flux is re-radiated as a black body

albedo (A)

the fraction of incident sunlight reflected by the object i.e. (1 - A) fraction of sunlight was absorbed

subsolar temperature

for slow rotating planets

absorbing area = emitting area

equilibrium temperature

for planets with atmosphere and/or in rapid rotation. assumes absorbing area is cross-sectional (πR²) and emitting area is the whole thing (4/3 π R²)

planetary atmospheres

assume atmosphere behaves like ideal gas with Maxwellian distribution of particle velocities:

most probably velocity v_mp = sqrt(2kT / m)

RMS velocity v_rms = sqrt(3kT / m)

standard deviation σ_v = sqrt(kT / m)

timescale of atmosphere loss is dependent on

ratio of v_esc / v_rms

timescale for different ratios

>10: billions of years

~5: few 100 years

~3: few years

~2: few days

use for radial velocity

as stars and planets orbit each other, their spectral lines are doppler shifted when they are moving towards/away from the observer. Exoplanets can be detected using the radial velocity (RV) curves of stars

radial velocity of a star

v_s,r = v_ssin(i) = 2πa_s / P

i - inclination

a_s - average distance of star from system CoM

P - binary system’s orbital period

centre of mass

M_pa_p = M_sa_s

orbital separation between a star and an exoplanet (a)

a = a_s + a_p = as ((M_s + M_p)/ M_p) = Pv_s,r / 2π

binary mass function

(M_p sin(i))³ / M_s² = P(v_s,r)³ / 2πG

exoplanet binary mass system (M_p << M_s)

M_p + M_s ~ M_s

(M_p sin(i))³ / M_s² = P(v_s,r)³ / 2πG

Star

an object bound by self gravity which radiates energy primarily released by nuclear fusion reactions in the stellar interior. When fusion is not dominant, stellar birth is too cold so GPE is radiated as radius of protostar contracts. During stellar death, the remnants radiate stored thermal energy and cool down.

composition of stars

expressed as ratios of gases over M_* of Hydrogen (X), Helium (Y) and metals/other elements (Z) such that X + Y + Z = 1

distance to stars

distance to nearby stars can be found using the parallax (apparent stellar motion due to orbit of star around earth)

parallax for small angles (radians)

θ = 1 AU / D (1 astronomical unit)

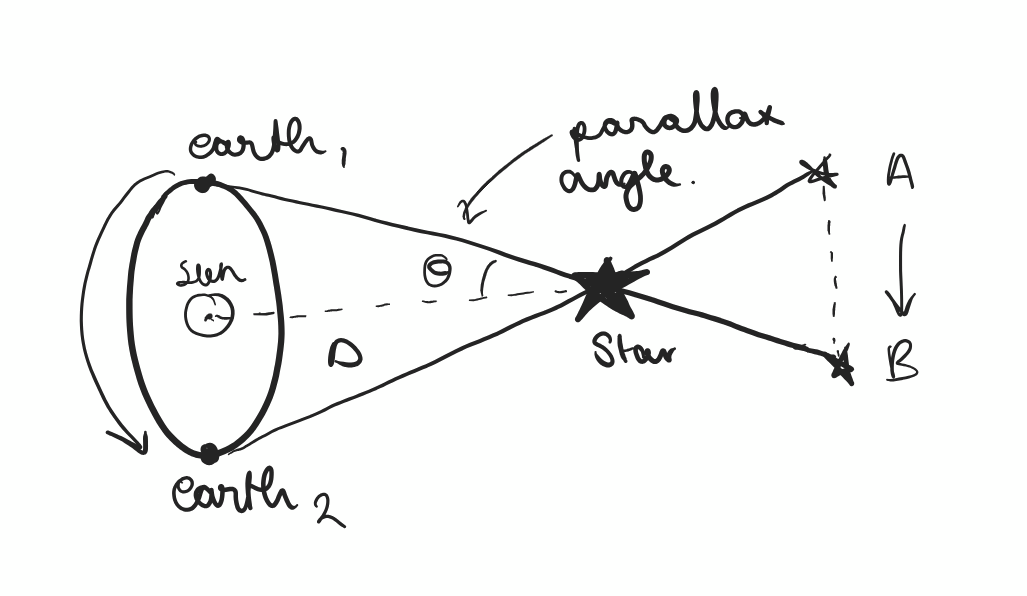
parallax in arcseconds

D = 1 / θ

Magnitudes

source brightness is expressed in Magnitudes (m) related to the source’s flux (F)

m = -2.5log₁₀F + constant

zero point

observed magnitude of star with F = 1

used to calibrate different telescopes with each other (the constant added onto the end of the magnitude equation)

bolometric magnitude

magnitude over all possible wavelengths

since F is total flux integrated over all wavelengths, m will be bolometric as well.

magnitude with colour filters (e.g. V)

m_v = -2.5 log₁₀F_v + constant

only certain wavelengths are considered

common colour filters

U (ultraviolet) ~ 365 nm

B (blue) ~ 440 nm

V (visible) ~ 550 nm

R (red) ~ 641 nm

K (infrared) ~ 2.2 μm

colour of star

the difference in magnitude of the two band passes e.g. B-V colour is m_B - m_V

colour/surface temperature of stars

stars radiate s black bodies, so colour reflects the surface temperature (hotter stars have smaller B-V band i.e. bluer colour)

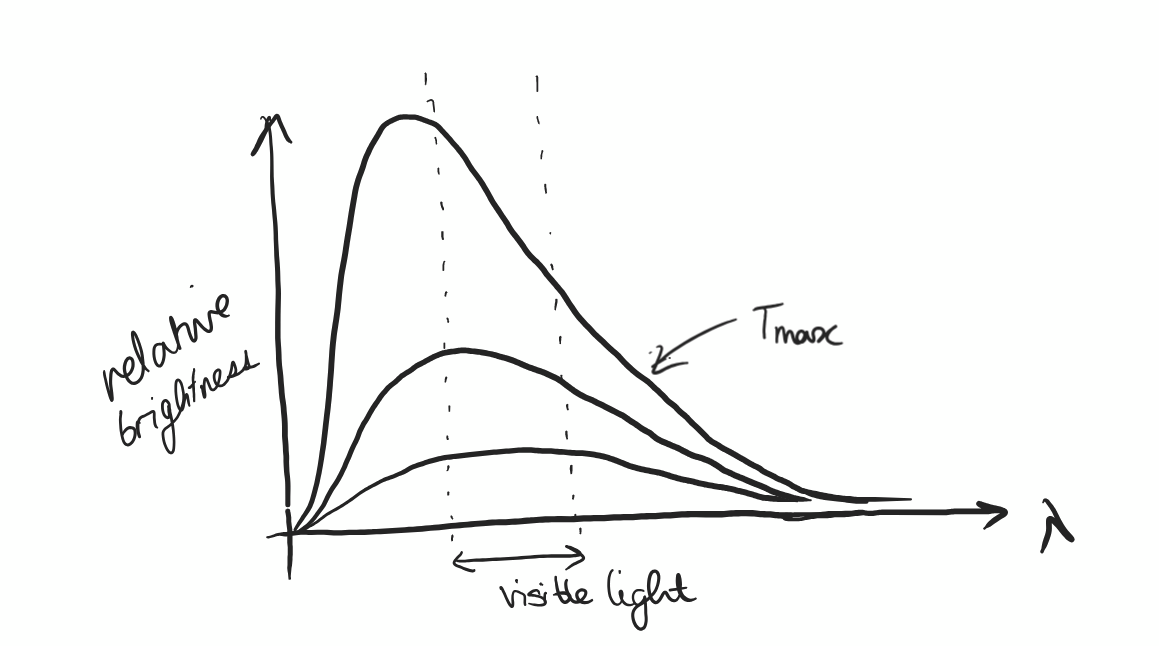
absolute magnitude (M)

apparent magnitude a source would have at a distance of 10pc (30.86e18 m). It is an intrinsic property of a source and a measure of luminosity in some waveband

distance modulus (μ)

difference between apparent magnitude (m) and absolute magnitude (M) [similar convention for flux f/F)

μ = m - M = 5log₁₀(d/10pc) = 2.5 log₁₀(F / f)

flux and luminosity ratio

2.5 log₁₀(F / f) = 2.5 log₁₀(L / l)

extinction

If light is attenuated between the source and the observer (e.g. due to interstellar/atmospheric extinction) the observed flux F(λ) at some given wavelength λ relates to the emitted flux F₀(λ):

F(λ) = F₀(λ) exp(𝜏_λ)

𝜏 - the optical depth (larger when material is more opaque)

extinction formula

m(λ) -m₀(λ) = 1.086 𝜏_λ = A_λ

A_λ - extinction (magnitudes), which is λ dependent (increasing with decreasing λ). This shows that extinction changes the colour of the source by making it redder

colour excess

How much attenuating material there is towards a given source

E(B-V) = (B-V) - (B-V)₀ = A_B - A_V

stellar mass

M* - a key property of stars used to determine a star’s evolution/life cycle

measuring M* using stellar spectrum

details in the absorption spectrum of stars depends on surface gravity g = GM / R². If we can measure g and R, M can be determined. Also, g ∝ 𝜌R, so stars of different densities will have different g value, which can be observed in collisional broadening in spectral lines

measuring M* using binary stars

Main way to measure stellar mass - use the properties of two stars in a binary system to determine M*

visual binary

each of the stars can be resolved individually.

If motion can be seen, then we can measure the ration of orbital radii a₁/a₂

M₁a₁ = M₂a₂ ⇒ a₁/a₂ = M₁/M₂ and so mass ratio can be determined

eclipsing binary

line of sight to observer lies in orbit so that forground star blocks light from background star. Only radius of these stars can be measured, not mass

spectroscopic binary (ratio of masses)

where we see periodic doppler shifts in the positions of the spectral lines from both stars in the binary, from which we can measure P, v_r,1 and v_r,2.

v_r,2 / v_r,1 = 2𝜋a₂/P / 2𝜋a₁/P = M₁ / M₂

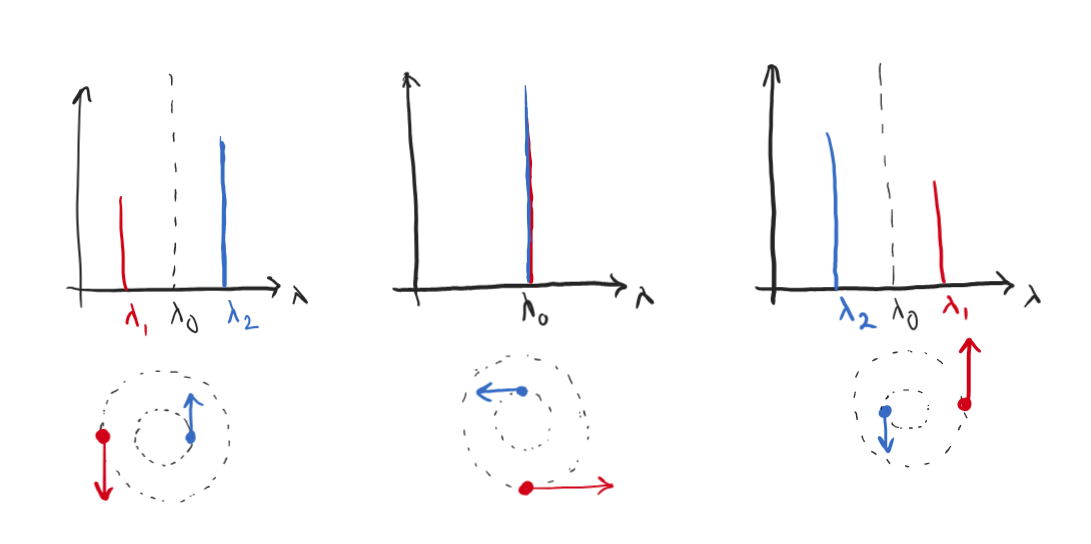
spectroscopic binary (sum of masses)

a = a₁ + a₂ = P/2𝜋 (v₁ + v₂)

⇒ M₁ + M₂ = (P/2𝜋G) (v_r,2 + v_r,1)³ / sin³i (from substituting into K3)

(you need to know the inclination i to find the sum of masses)

grav acceleration on test particle distance r away from body of mass M

a_grav = GM / r²

differential of grav acceleration felt by 2 different test particles at different locations

da_grav = -(2GM / r³) dr

strength of tides

differential of grav acceleration can be translated to macroscopic bodies to tell us the strength of tides exerted by body of mass M on a second body of size R_m at distance d:

∝ MR_m / d³

Roche Limit

tides slow down rotation and can lead to tidal locking, or even disruption of satellite. Roche limit is max distance at which satellite of density 𝜌_m (held together by self gravity) is torn apart by tidal forces from primary body of size R_M and density 𝜌_M