DM - 7: Axiomatisation: Peano Arithmetic

Peano’s definition of the set of natural numbers.

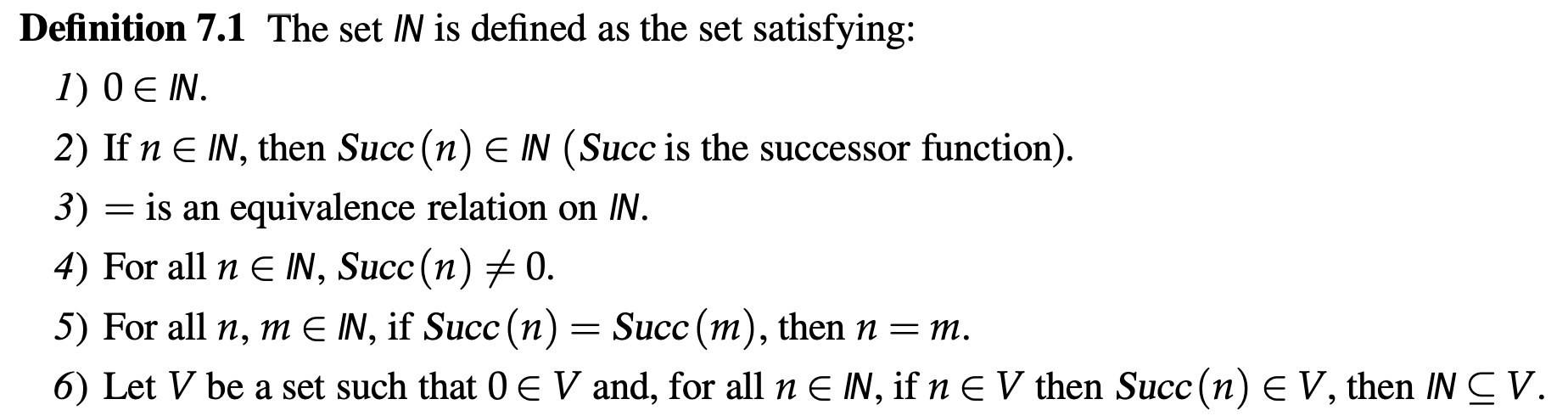
Define mathematical induction

Why does induction work?

It is a closure property;

It is true that this way we can construct a proof for P(n), for every n, but it is not true that we have a proof that ∀n ∈ IN (P(n)) holds; the “and so on” path is infinitely long, and we do not accept infinitely large proofs.

Instead, mathematical induction over IN is possible, i.e. an accepted proof step, purely thanks to the fact that we assume that IN is the smallest set containing 0 and being closed under Succ.

Defining Add and Mult over Natural numbers

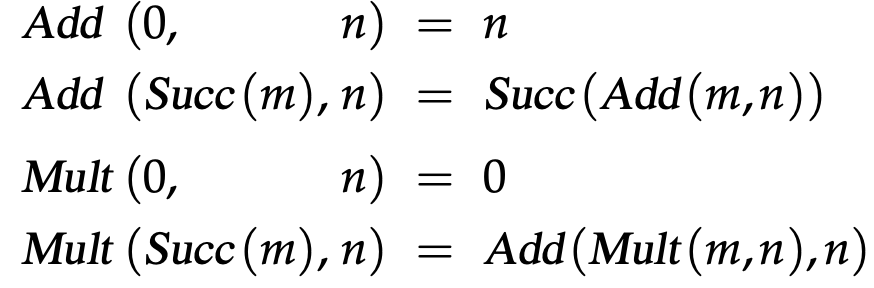
How do we define the set of integers starting from the set of natural numbers?

How can we define a smaller-than relation <1 on numbers?

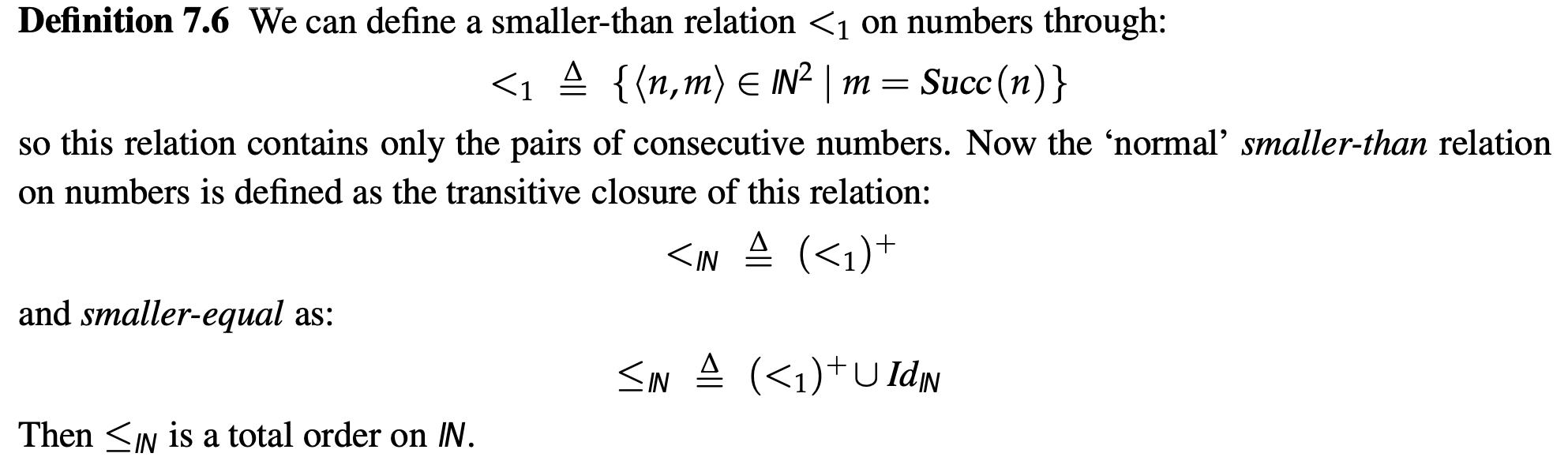
For any set A, the power set of A ordered by subset inclusion, (℘A,⊆), is…

…a partial order.