MMW 3&4

lessons 3 & 4

mathematical language

system used to communicate mathematical ideas

precise

able to make fine distinctions

concise

able to say things briefly

powerful

able to express complex thoughts with relative ease

variables

letters used as placeholder

expression

finite combination of symbols

sentence

statement about two expressions

mathematical convention

usage which is generally agreed upoPEMDAS or BODMAS

set theory

branch of mathematics that studies sets

george cantor

german mathematician who is considered as the founder of set theory

set

well-defined collection of objects

elements or members

objects of the set

{}

“set of”

E

“element of” or “belongs to”

E/

“not an element of” or “does not belong to”

x|x

“…set of all x’s such that x is…”

roster method

• also called tabulation method

• elements of the set are enumerated and separated by a comma

rule method

• also called set builder notation

• descriptive phrase used to describe elements

finite set

set whose elements are limited or countable

infinite set

set whose elements are unlimited or countable

unit set

• also called singleton

• set with one element

empty set

• denoted by ∅ or { }

• also called null set

• unique set with no elements

universal set

• denoted by Ω or U

• set of all sets

cardinality

• denoted by n{N}

• cardinal number of a set is the number of elements in the set

subset

• denoted by ⊆

• collection of elements contained inside another set

not a subset

denoted by ⊄

proper subset

• denoted by ⊂

• subset if suppose set B contains at least one element that is not present in set A

improper subset

• denoted by ⊆

• subset which contains all the elements of the original set

equal sets

• denoted by =

• if each element of set A is also the element of set B

equivalent sets

• denoted by ~

• if both have the same cardinality (number of elements)

joint sets

when sets have at least one common element

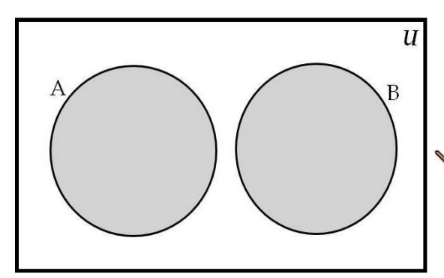
disjoint sets

when sets have no common element

powerset

• denoted by P(S)

• set of all subsets of a given set

venn diagram

pictorial presentation of relation and operation on set (set diagram)

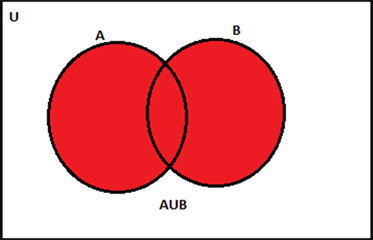
union

• A U B

• in set A/set B/both

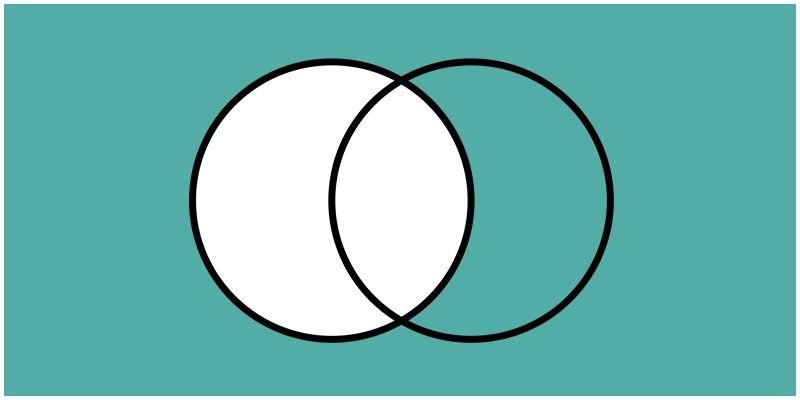
intersection

• A n B

• in A and B

complement

• A’ or B’

• all in the universal set except them

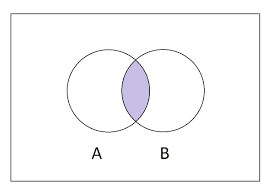
difference

• A - B

• relative complement, all in A not in B

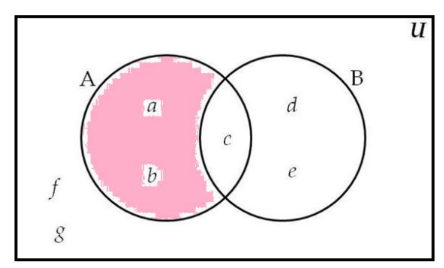
symmetric difference

• A ⊕ B

• belongs in A or B but not in both

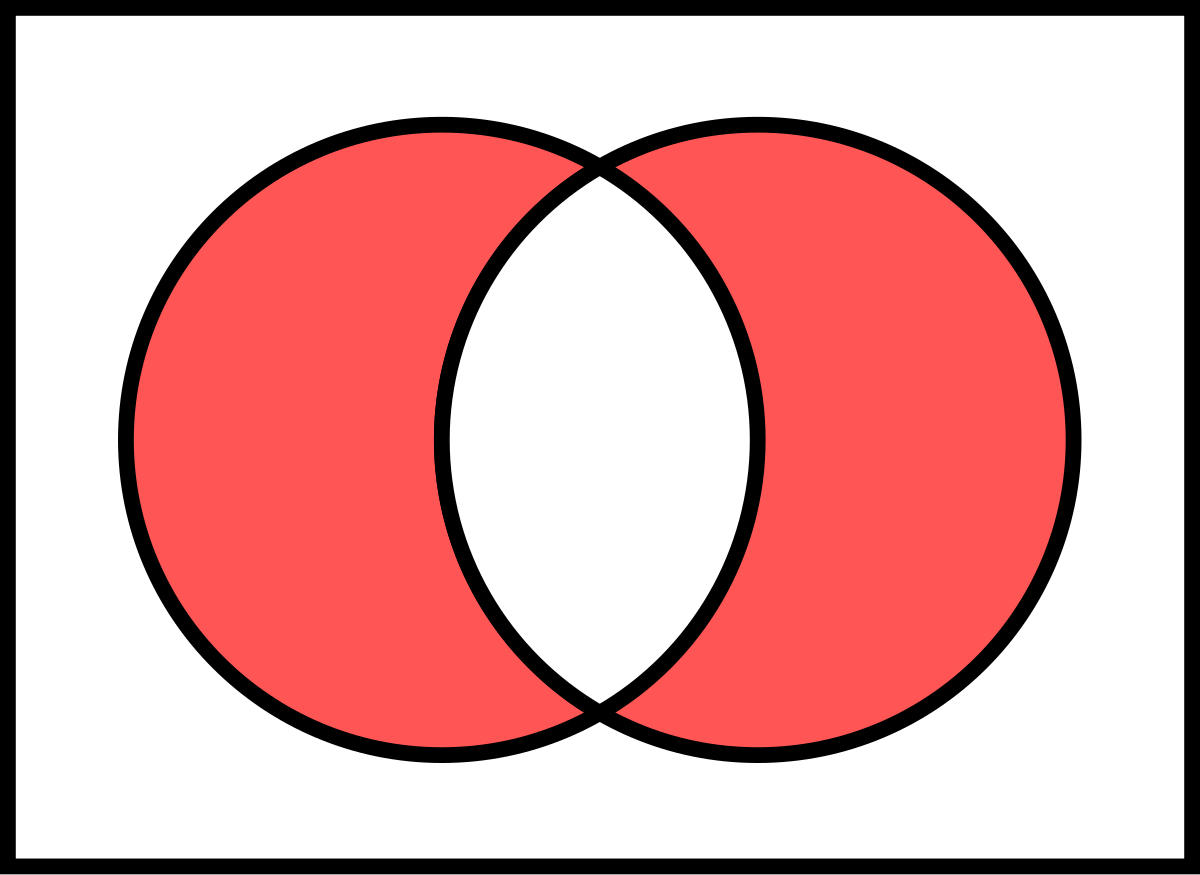
disjoint

• A n B = Ø

• if and only if they have no elements in common

• also called non-intersecting

ordered pair

• (a, b) = (a, b) and (a, b) ≠ (b, a)

cartesian product

• A x B

• also called cross product