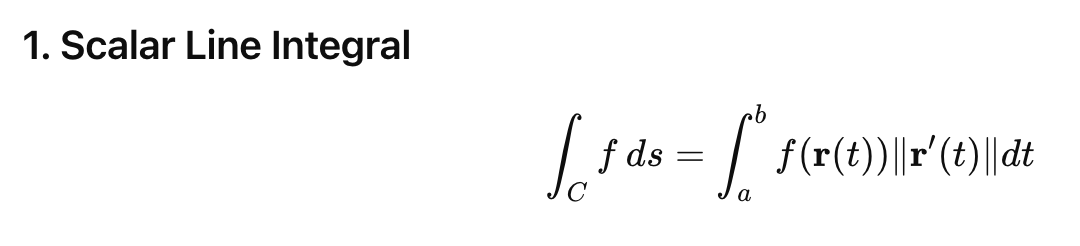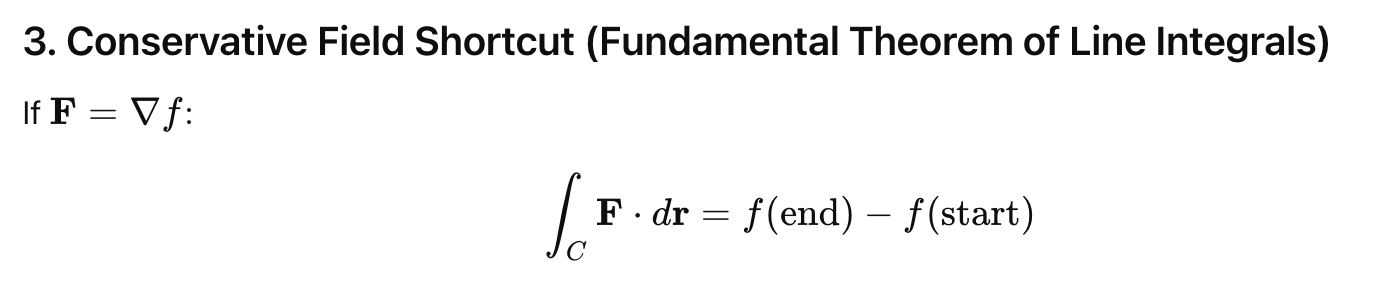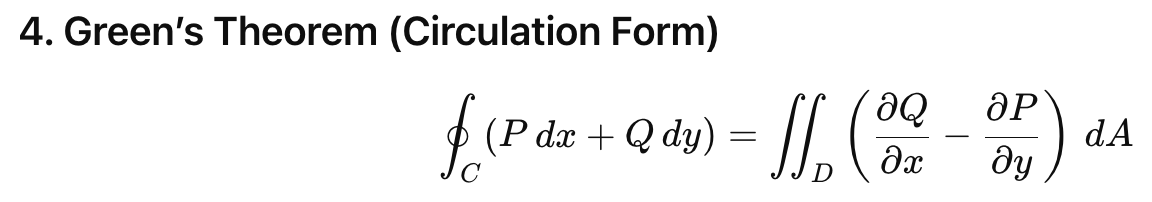Multivariable Calculus Lecture 12

Divergence: measurement of how much fluid/flow enters the neighborhood around “P” compared to how much leaves

• if more fluid/flow enters the nei. than leaves it, then divergence will be ___ (gathering)

• if the same amnt of fluid/flow enters and leaves, then divergence will be __ (incompressible)

• if more fluid leaves than enters then divegence will be ___ (diverging)

-, 0, +

Div F =

scalar

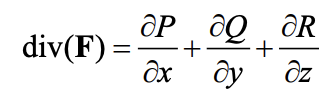
Curl: measurement of rotation of VF in nei around P

• if curl __, then rotate counterclockwise at P

• if curl __, then rotate clockwise at P

• if curl = __, no rotation at P

+, -, 0

curl(F)

you write in P, Q, R

ans is vector

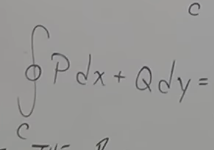
Green’s theorem: deals with line ∫ of simple closed curves over non-conservative vector fields

if over conservative vector field…

W = 0

How to use green’s theorem

1. draw ____

2. label __ & __ in the line integral expression (components of vector field F(x,y))

3. write out double integral ∫ ∫R ∂Q/∂X-∂P/∂y dA and fill in _____

   1. If you get 0 for ∂Q/∂X-∂P/∂y, then the vector field is ____ and the work done = __

4. Find the ___ and finish writing the double integral

5. integrate

curve/region

P, Q

∂Q/∂X-∂P/∂y

conservative, 0

region

area of ellipse

abπ

Area of region enclosed by curve

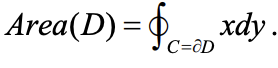
Using green’s theorem, if you get ∫ ∫R 1 dA from step 2, the line ∫ =

area of region

When to use each line integral/work equation

1. If the integral is of a scalar density (like mass):

2. If the integral is over a nonconservative vector field:

3. If the integral is over a conservative vector field:

4. If the integral is of a simple closed curve over nonconservative vector field