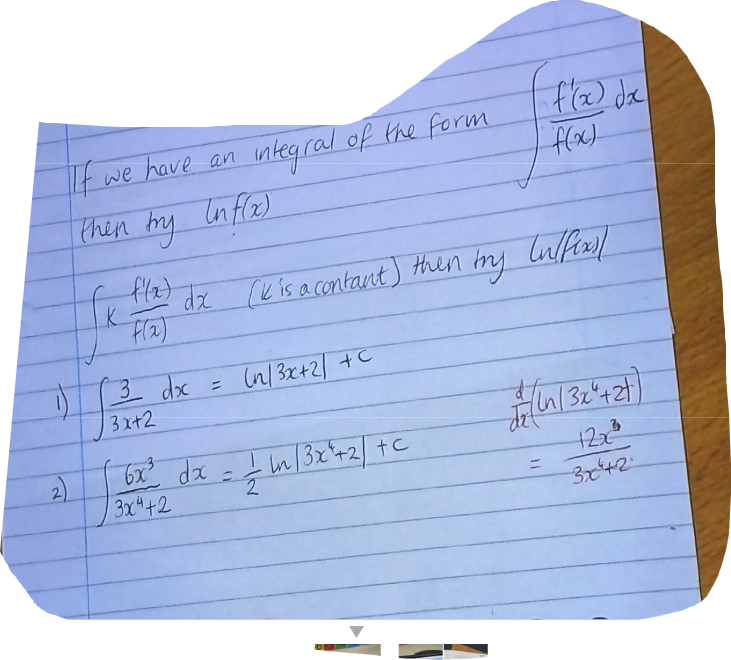11 - integration

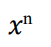
integrate this

.

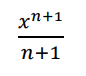
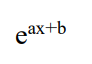
integrate this

.

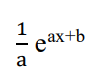
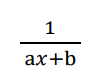
integrate this

and if the top is anything other than 1, replace the 1 on the answer as well!

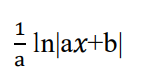
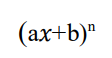
integrate this

.

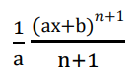
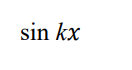
integrate this

and if its cos(kx + b) just put + b on the end

before the + c duh

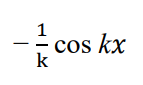
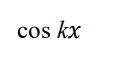
integrate this

and if its sin(kx + b) just put + b on the end

before the + c duh

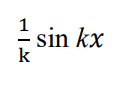
integrate this

.

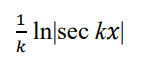
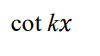
integrate this

.

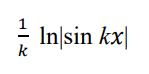
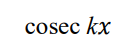
integrate this

.

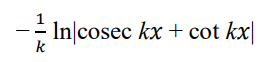
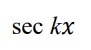
integrate this

.

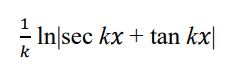
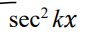
integrate this

.

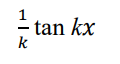
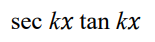
integrate this

.

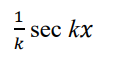
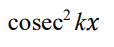
integrate this

.

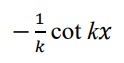
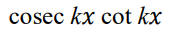
integrate this

.

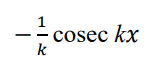
what not to forget after all integrals

+c !!!

why modulus when it comes to ln

can’t find ln of a negative number

when you integrate, your answer for an area should always be…

….positive!

what to remember when simplifying integrals involving ln

log laws! dividing and subtracting, multiplying and adding, powers, etc etc

what’s one thing you are allowed to do with integral equations

factorise:

the integral of 2x³
is the same as saying
2 x the integral of x³

how to integrate something in the form f’(ax+b)

use the reverse chain rule!

eg. the integral of cos(2x+3) is 0.5sin(2x+3) + c

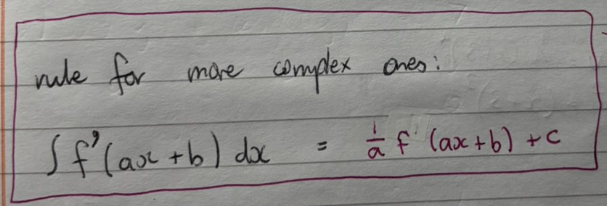
what’s the longer version of the reverse chain rule

integration by substitution

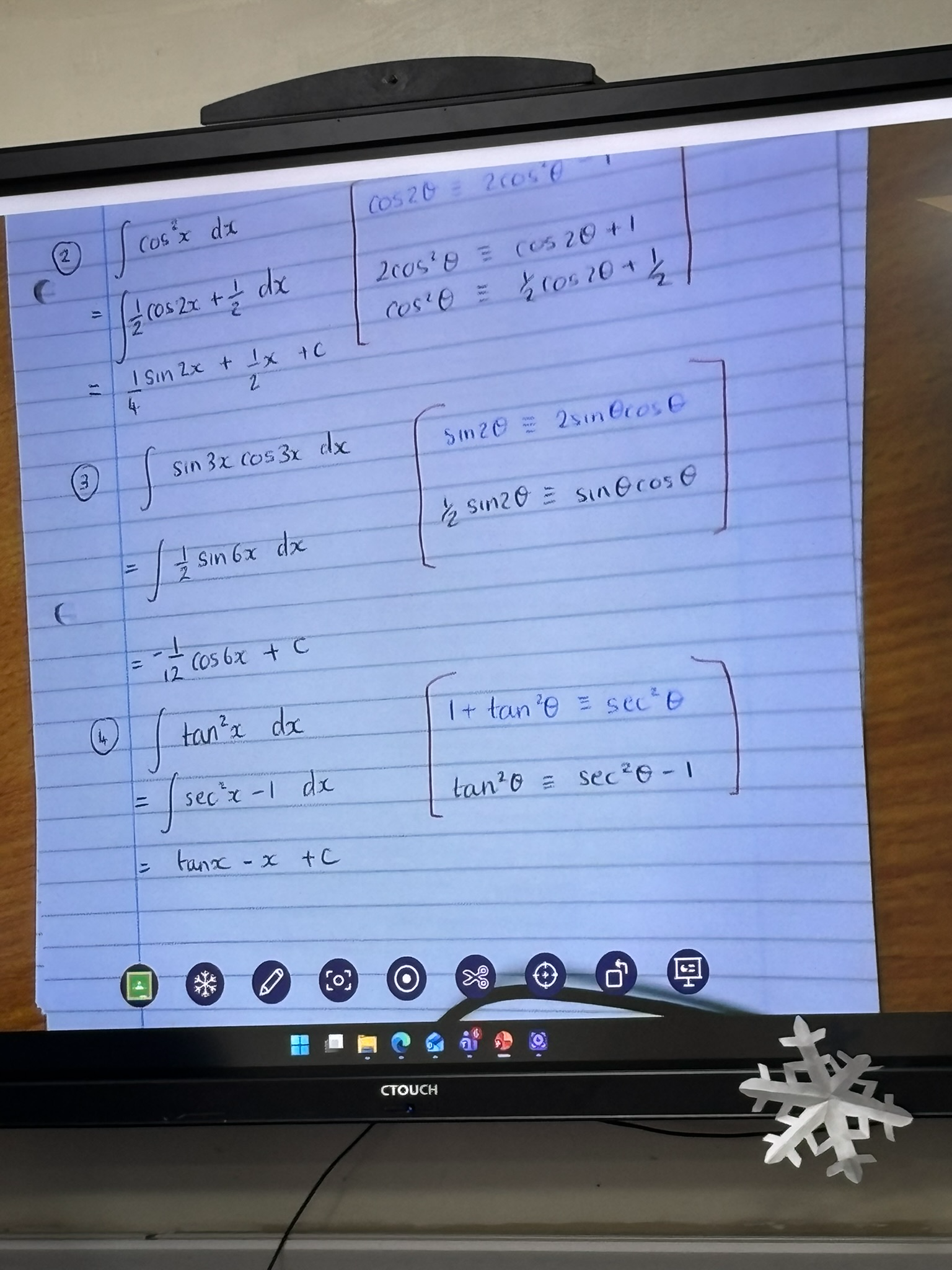
what do u have to do if an integration has a trig identity thats not immediately solvable like

2sin²× 2sinxcosx

etcetc

use trig identities to rewrite into something u can solve

eg. with the given examples that would be:

1-cos2x
sin2x

more examples pictured

what do we use to integrate the product of two functions, and what’s the formula for that?

integration by parts

formula in the formula booklet but also pictured

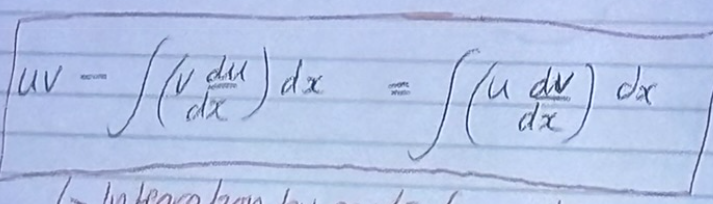
how was the integration by parts formula made

integrated the differentiation product rule

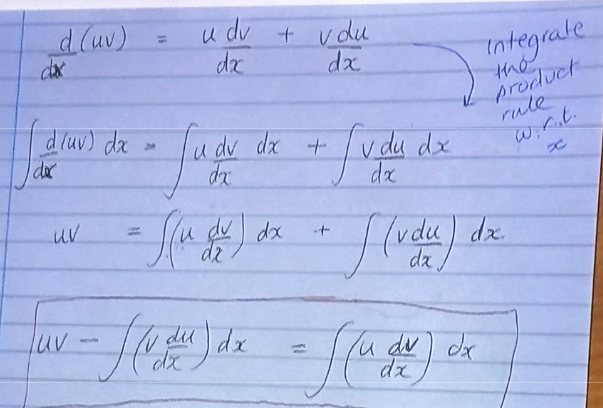
how to use integration by parts formula

STEP 1 - choose who will be u and dv/dx

priority for choosing dv/dx is this:

Logarithms
Algebra
Trig
Exponentials

and if they are the same then simplest first

STEP 2 - write out who v and du/dx is

use the u and dv/dx values from above and integrate/differentiate accordingly

STEP 3 - factorise to simplify

integrate this:

lnx

xlnx - x (+c)

method pictured (uses the product rule!)

when you get an answer with many parts in log form what to do

simplify as much as possible into one part

what to do in a situation where multiplying v and du/dx would need u to use integration by parts (so its like a cycle)

replace u and dv/dx with a single variable (pictured example = i)

then solve for i

then set i equal to what it originally was (u and dv/dx)

then solve

then rewrite it all together

MUCH clearer in the picture and in practice……

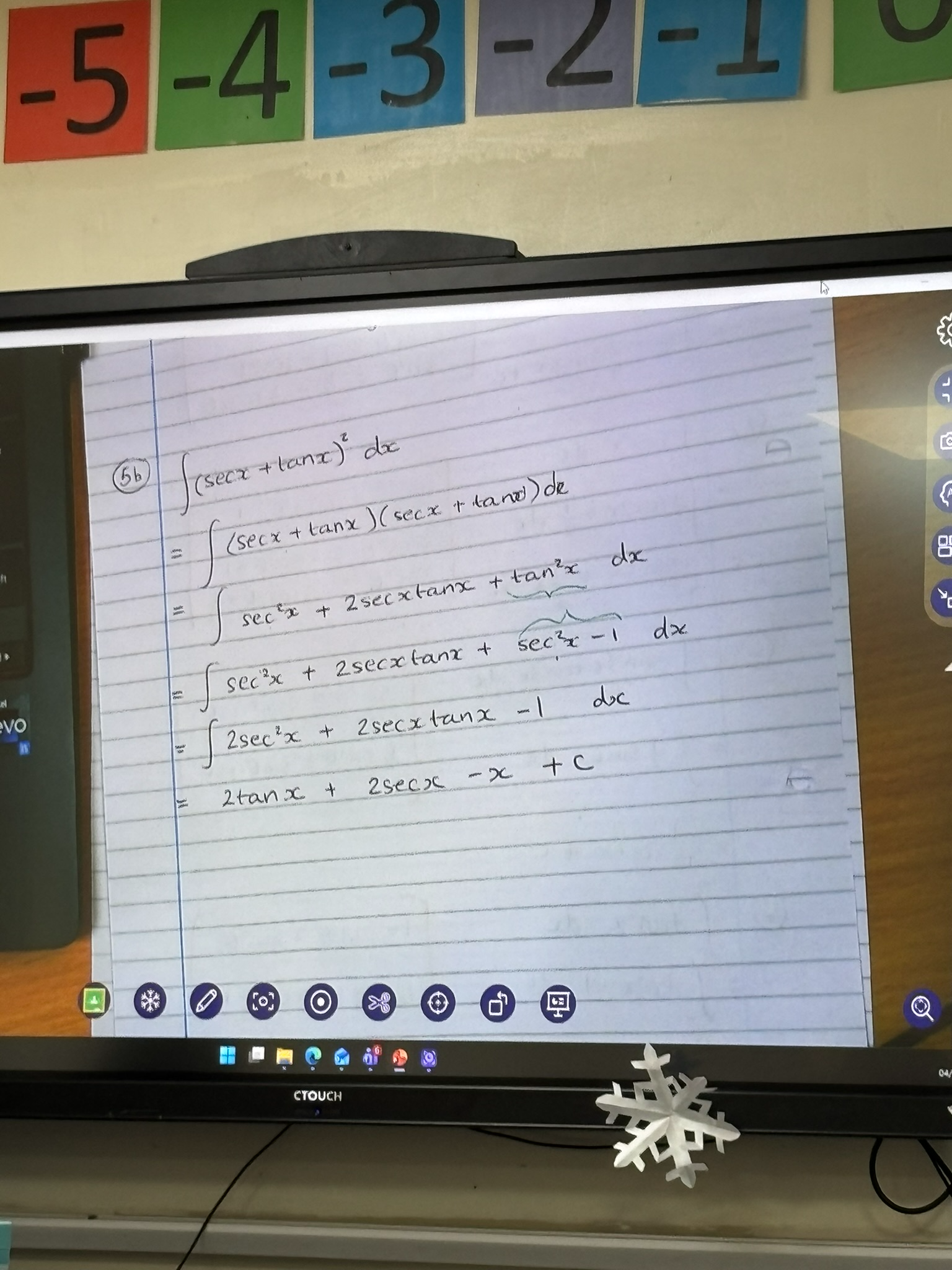
something to look out for in integration questions

squares, or difference of two squares

always expand then solve (example pictured)

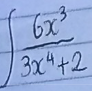
when you have to integrate a function that looks like this, how to approach

try the ln of the denominator

then multiply it by what’s necessary to make it have started at the right place so u can differentiate to check and its fine (very badly worded but clearer in practice and in the pic)