Questions DT

ANN - Why the dataset for training is typically divided into three parts (training validation test)?

The dataset is divided into three parts:

·         Training set, which is used to adjust the weight of the synapses

·         Validation set, which is used for validation as the name implies. It fundamentally checks each iteration for error, on the validation set after the weight adjustment (which occurred in the training set).

·         Test set is used as a performance check using data never seen during the training.

Thus, to summarise, the training set adjusts synapse weight, validation set verifies adjusted synapse weight error, and the test set tests the new synapse weight on new data.

ANN - Explain one method for training (and what does it mean training an ANN)

·         One method of training is via the supervised training framework.

·         Uses set of network inputs, for which the desired network outputs are known to optimise synapse weights.

·         At each step, set of inputs is passed forward through the network and trial output is obtained, and then compared with known output (target)

·         If significant error found, used to adjust synapse weight to minimise error

·         Optimisation strategy needed, for finding weight (w), dependent on error (E) between target (t) and ANN (y) outputs.

·         Training the ANN fundamentally means optimising the weight of the synapses.

ANN - Where does the term “error back-propagation” come from?

·         Error back propagation is a gradient descent method used in the context of ANN training.

·         Within the back-propagation algorithm, an expression is found for the Error, Error gradient w.r.t. output layer weights, and an Error gradient w.r.t. hidden layer weights.

·         Error function to be minimised during training

·         ANN learning can be associated with problem of maximum likelihood estimation, which can be applied to both regression and classification problems.

ANN - Explain the need for data balancing

·         Imbalanced data = data with overrepresented and underrepresented subsets

·         Needed because imbalanced dataset can result in a biased model, poor performance metrics, overly sensitive to majority class neural networks.

·         Techniques for balancing include oversampling and undersampling

ANN - Explain the need for data normalization

·         The data should be normalised before training an ANN

·         This is since the same order of magnitude is required, due to activation function within ANN. Thus, if input is too big, output can’t be reconstructed.

·         Z-score normalisation and min max scaling are the most common techniques.

ANN - Explain the concept of overfitting/overtraining

·         Overfitting happens when the algorithm, via attempting to minimise error, not only learns significant features but also noise.

·         This can happen if ANN structure is too complex, or if the training procedure runs for too long (overtraining)

ANN - How can we identify overfitting/overtraining during the ANN optimization?

·         Quantitatively, via an increase in validation error whilst training error decreases

·         Qualitatively, by simply observing the graph and checking how much of the noise is replicated by the ANN output.

ANN - Explain the concept of ANN generalization

·         Capability of a trained ANN to learn significant features inside a certain training pattern.

·         Thus, being capable to generalise, or to use gained information when new pattern is processed.

ANN - ANN was proposed as a means for surrogate modelling, why?

·         A surrogate model runs much faster and mimics the behaviour of a physics-based model.

·         It allows for faster analysis or optimisation by replacing the original model with a simpler one.

·         Fundamentally, the above allows for the implementation of a DT which often requires “live” analysis.

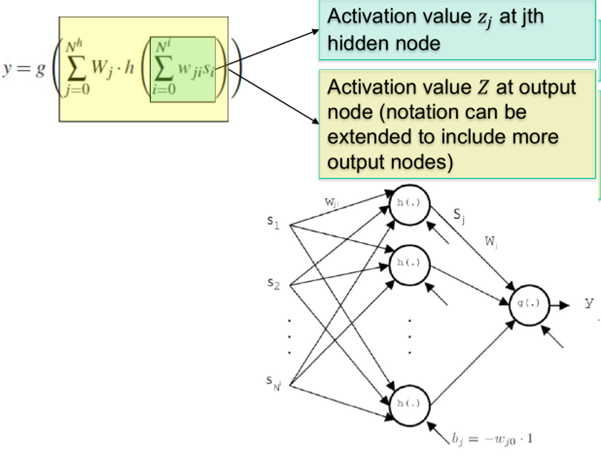
ANN - Show the structure and the mathematical formulation of a multi-layer perception

Input layer

·         Neurons that receive as input data to be processed and distributed as input signals to the first available layer of computing neurons

Hidden layer

·         Intermediate neurons that process data from other neurons and provide input to consecutive layer.

·         No external communications

Output layer

·         Neurons that provide final output of network

BAYES THEOREM - Explain its usage in model-updating

·         Bayesian approach naturally applicable to describe statistics in model updating.

·         Used to update system parameters via Bayesian algorithms for parameters estimation, such as MH MCMCM (Markov Chain Monte Carlo).

BAYES THEOREM - Why Bayesian inference is well-suited for the solution of inverse problems?

·         Bayesian approach treats probabilities as beliefs, not frequencies

·         Parameters treated as pdf

·         Unknown parameter is given a prior distribution representing prior beliefs

·         After seeing observations, Bayesian approach computes conditional posterior distribution for unknown parameter given the observation using Bayes’ theorem

·         It then calculates the likelihood, and using this the Bayes’ theorem transforms the solution of inverse problems into multiple direct problems.

BAYES THEOREM - Explain why the following sentence is true: "Bayes theorem transforms solution of inverse problems into multiple direct problems"

·         After seeing observations, Bayesian approach computes conditional posterior distribution for unknown parameter given the observation using Bayes’ theorem

·         It then calculates the likelihood, and using this the Bayes’ theorem transforms the solution of inverse problems into multiple direct problems.

BAYES THEOREM - Explain the Bayes' Theorem Formula

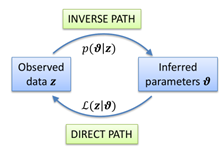
BAYES THEOREM - Observed data, inferred parameters, inverse path and direct path: how are they correlated?

·         Observed data and inferred parameters are linked  via the likelihood and Bayesian updating

·         Direct path and inverse path form a cycle

BAYES THEOREM - Explain the challenge related to the calculation of the likelihood term

·         Some models have no analytical likelihood (implicit models, stochastic processes)

·         Others may have non-differentiable likelihoods, or likelihoods with numerical instability

MCS - Why/when do we need Monte-Carlo sampling in the context of model updating?

·         We use it to find the posterior Bayesian via samples which approximate it

·         We use it to compute the expected values, since MC approximates integrals by averaging over samples

·         MC allows forward propagation of parameter uncertainty

·         Computing the marginal likelihood.

MCS - Explain the concept of “curse of dimensionality”

·         The curse of dimensionality is that increasing the domain dimensionality requires a lot of samples for the PDF approximation.

·         It fundamentally refers to the better-known concept of “diminishing returns” and here it basically implies that after a certain point, more features or dimensions no longer improve the model’s performance but require a lot of samples and processing power.

·         Dimensionality can be reduced via PCA

MCS - Why do we need importance sampling?

·         We need important sampling to make sampling more efficient.

·         Use the least number of samples to produce the best approximation of expectation with the smallest uncertainty.

MCS - In which problems did we encounter importance sampling?

·         In case where the expectation is dominated by regions of small probability.

·         Where a lot of samples are required to guarantee a sufficient scan of the support, and thus, to achieve sufficient accuracy in estimation of the expectation.

·         Used in calculating the cost of the lifecycle model

MCS - Explain the MCMC-MH procedure and the requirements (models and hyperparameters) for its implementation

Initialisation

·         Select prior for parameters

·         Select proposal pdf

·         Select starting point of MC and compute prior, and likelihood of measurements given the parameters

Draw random, tentative sample from proposal

Compute prior probability and the likelihood of measurements given tentative proposed sample

Compute likelihood and prior ratio

Accept the tentative proposed sample as the next state in the Markov chain

Repeat from 2 to 5 until desired chain length reach

Erase burn in period and thin the chain

We have samples for probability of parameters given the measurements

Hyperparameters

·         Burn in period

·         Chain length

·         Thinning

Model

·         Likelihood

·         Prior

·         Posterior proportional to Likelihood x Prior

MCS - Can you synthetically describe the path followed during the course for digital twinning, linking Bayesian inference, Monte Carlo Sampling and surrogate modelling?

·         Began with analytical approaches, including classic elastic fatigue analysis and Linear Elastic Fracture Mechanics (LEFM)predict crack propagation and failure in pressure vessels using Paris’ law and stress intensity factors.

·         Discrete event system (SimEvents) simulated operational loads and defect generation, employing Monte Carlo sampling to assess failure risks and costs, later refined via importance sampling for variance reduction.

·         Accelerate simulations, a surrogate model (ANN) was trained to replicate a Simscape-based leakage model.

·         Bayesian inference (MCMC-MH) was applied to infer the true leakage area from noisy sensor data, using the ANN surrogate for likelihood evaluation and a Weibull prior.

General - Which are the requirements of a digital twin for Health and Usage Monitoring and which methods have been shown during the course to meet those requirements?

Contain information about degradation processes

·         Classic Elastic and LEFM

·         Discrete event sim

Fast enough to guarantee real time

·         ANN surrogate

Must be adaptive and self-updating

·         Bayesian (MCMC – MH)

Must be stochastic

·         MC and Importance sampling