AP Calculus AB Formulas

All formulas for AP Calculus AB exam. It's long, God bless our souls.

Definition of e

e = limn→∞ (1 + 1/n)^n (where e is the base of the natural logarithm)

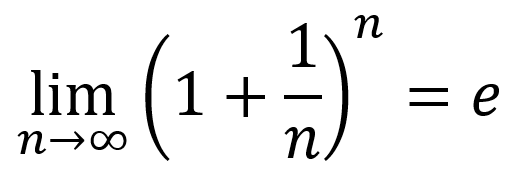
Definition of absolute value

|x| = x if x ≥ 0, -x if x < 0

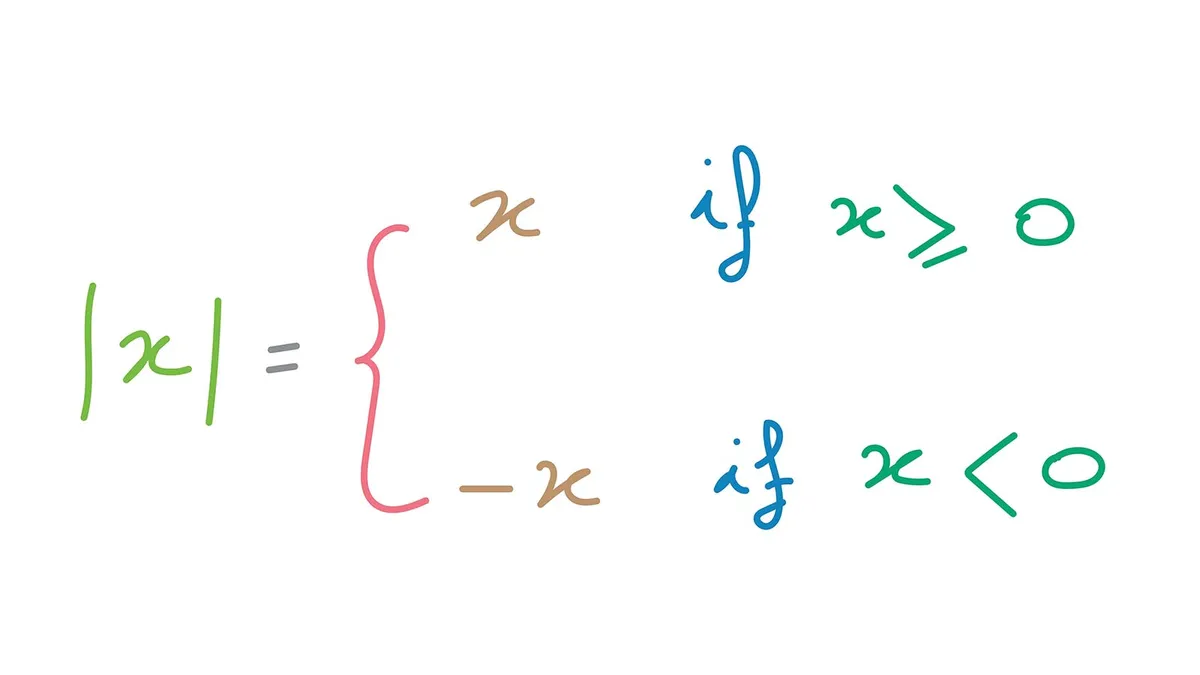
Definition of the derivative

f’(x) = limh→0 (f(x+h) - f(x))/h

f’(a) = limh→0 (f(a+h) - f(a))/h

Alternative form of derivative

f’(c) = limx→c (f(x) - f(c))/(x - c)

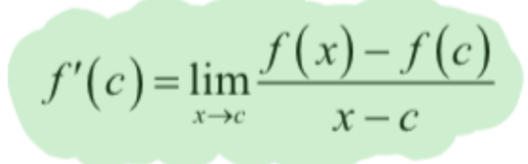
Definition of continuity

f is continuous at x = a only if

1. f(a) is defined

2. limx→a f(x) exists

3. limx→a f(x) = f(a)

Make sure to clearly state each part of this for FRQs

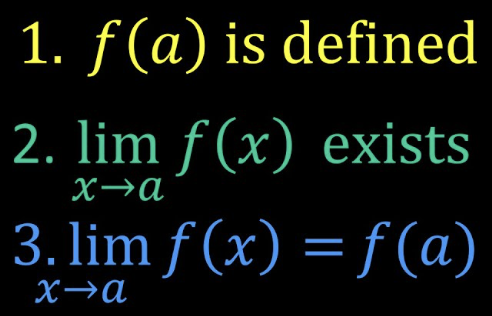
Average rate of change of f(x) on [a, b]

(f(b) - f(a))/(b-a)

Intermediate Value Theorem (IVT)

If f is continuous on [a, b] and k is any number between f(a) and f(b), then there is at least one number c between a and b such that f(c) = k

Rolle’s Theorem

If f is continuous on [a, b] and differentiable on (a, b) and if f(a) = f(b), then there is at least one number c on (a, b) such that f’(c) = 0

Mean Value Theorem (MVT)

If f is continuous on [a, b] and differentiable on (a, b), then there exists a number c on (a, b) such that f’(c) = (f(b) - f(a))/(b-a)

Pythagorean Trig Identities

1 - sin²x = cos²x

1 + tan²x = sec²x

1 + cot²x = csc²x

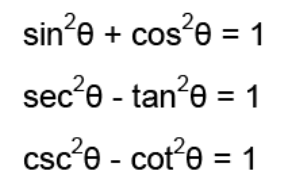
Double Angle Trig Identities

sin(2x) = 2sinxcosx

cos(2x) = cos²x - sin²x, 1 - 2sin²x, 2cos²x-1

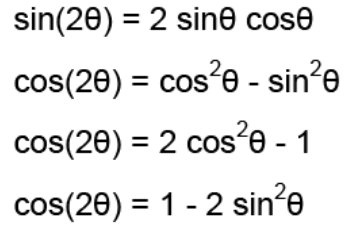
Derivative of a constant

d/dx (c) = 0

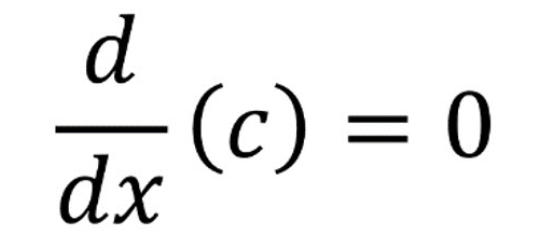
Derivative of function x function (Product Rule)

d/dx [f(x)g(x)] = f'(x)g(x) + f(x)g'(x)

Derivative of function / function (Quotient Rule)

d/dx [f(x)/g(x)] = (f'(x)g(x) - f(x)g'(x))/(g(x))²

Memorization Aid:

(lodehi - hidelo)/lo²

Derivative of Composite Function (Chain Rule, function inside of function)

d/dx [f(g(x))] = f'(g(x))g'(x)

Derivative of Function with Power (Power Rule)

d/dx [x^n] = nx^(n-1)

Derivative of Trig Functions

d/dx [sin(x)] = cos(x)

d/dx [cos(x)] = -sin(x)

d/dx [tan(x)] = sec²(x)

d/dx [csc(x)] = -csc(x)cot(x) d/dx [sec(x)] = sec(x)tan(x) d/dx [cot(x)] = -csc²(x)

Derivative of Logarithms

d/dx [ln(x)] = (1/x)x’
d/dx [log_a(x)] = (1/(xln(a)))x'

Derivative of Exponential Functions

d/dx [e^x] = (e^x) x’

d/dx [a^x] = (a^x ln(a)) x’

Derivative of Inverse Function

d/dx [f⁻¹(x)] = 1/(f'(f⁻¹(x))) x’

Critical Number

All x values for which f’(x) = 0 or is undefined

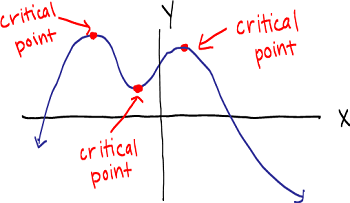
First Derivative Test - can be used to find relative mins and maxes

Function must be continuous & differentiable on open interval containing c (critical number(s))

1. Identify all critical numbers

2. Test values around critical numbers

3. Evaluate sign of derivative around critical numbers

If f’(x) changes from negative to positive at x = c (negative at values immediately less than c and positive at values immediately greater than c), then (c, f(c)) is a relative minimum. If f'(x) changes from positive to negative at x = c (positive at values immediately less than c and negative at values immediately greater than c), then (c, f(c)) is a relative maximum.

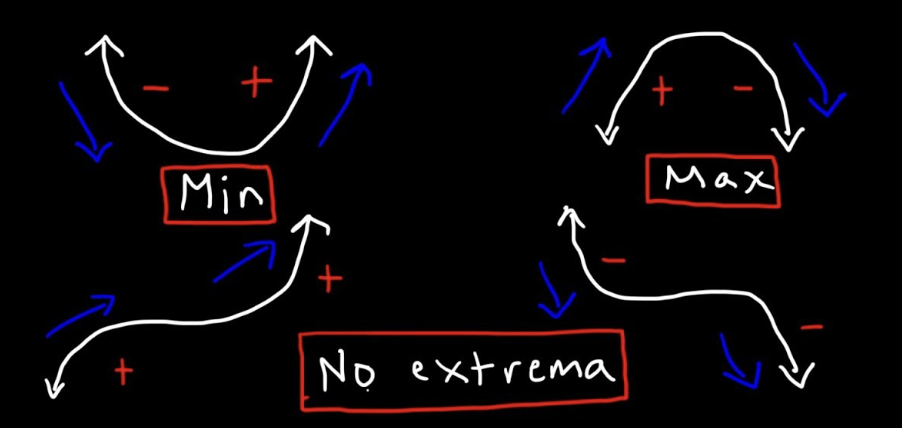
Second Derivative Test - also can be used to find relative mins and maxes but generally make-your-life-harder-method so use less

Function must be differentiable on open interval containing c

1. Identify all critical numbers

2. Input into second derivative

If f’’(c) > 0, then (c, f(c)) is a relative minimum. If f’’(c) < 0, then (c, f(c)) is a relative maximum.

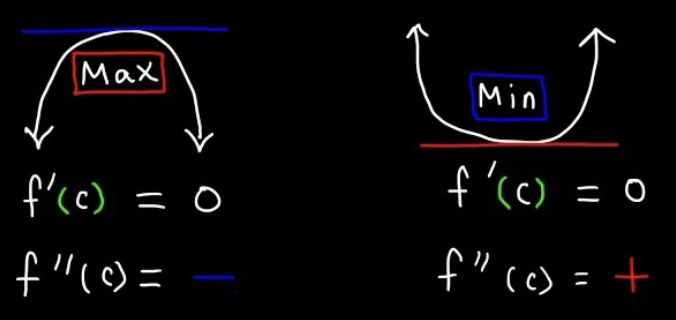
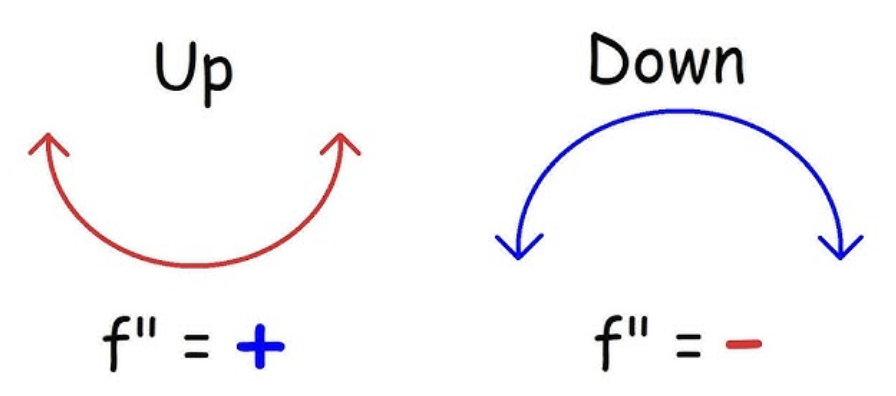
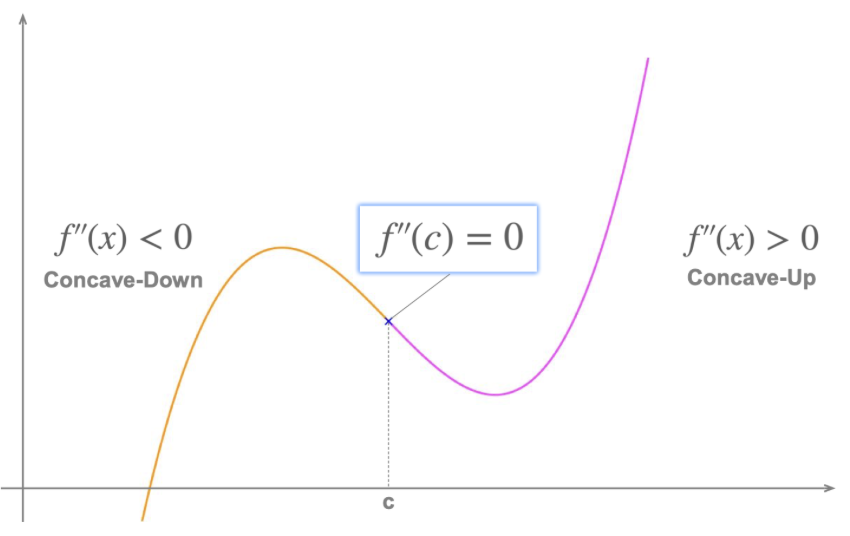
Definition of Concavity

Function must be differentiable. Opening and concave upward if f’’ is positive & opening and concave downward if f'' is negative.

Inflection Point

Point on function where second derivative of function is 0 or DNE and the concavity changes. Function has inflection point at (c, f(c)) if

1. f’’(c) = 0 or DNE AND

2. f’’ changes sign from positive to negative or negative to positive at x = c

Can be found by testing values immediately around c and inputting them into second derivative to see if output is +/-

Definition of definite integral

( \int_{a}^{b} f(x) \,dx )

limdeltax→0 \sum{i=1}^{n} f(xi^*) * Delta x

limn→infinity \sum{i=1}^{n} f(xi^*) * Delta x

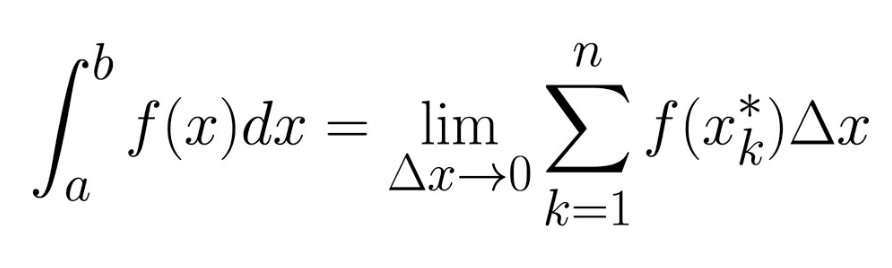
Integral of function with power

(x^(n+1))/(n+1) + C

Integral of trig functions

\int \sin(x) \, dx = -cos(x) + C

\int \cos(x) \, dx = sin(x) + C

\int \sec²(x) \, dx = tan(x) + C

\int \csc²(x) \, dx = -cot(x) + C

\int \sec(x)tan(x) \, dx = sec(x) + C

\int \csc(x)cos(x) \, dx = -csc(x) + C

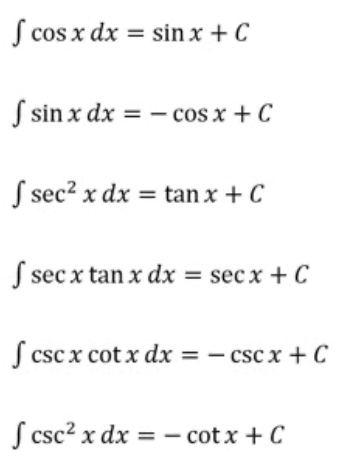
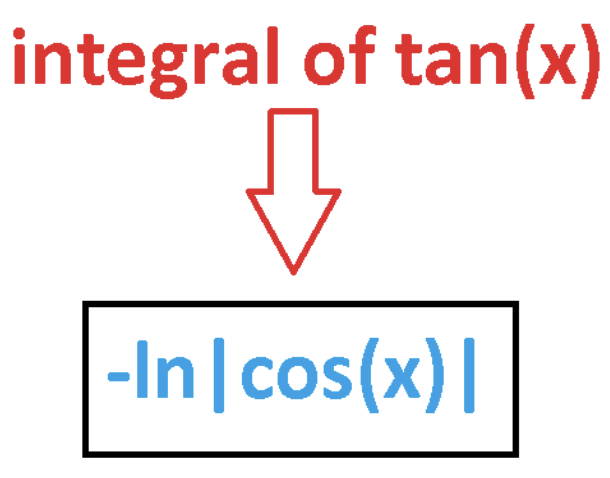
Integral of slightly more special trig functions

\int \tan(x) \, dx = -ln|cos(x)| + C

\int \cot(x) \, dx = ln|sin(x)| + C

\int \sec(x) \, dx = ln|sec(x) + tan(x)| + C

\int \csc(x) \, dx = -ln|csc(x) + cot(x)| + C

Integral of 1/x

ln|x| + C

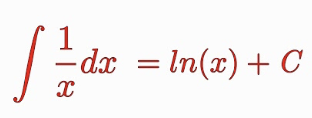
Integral of exponential function

\int e^x \, dx = e^x + C

\int a^x \, dx = (a^x)/lna + C

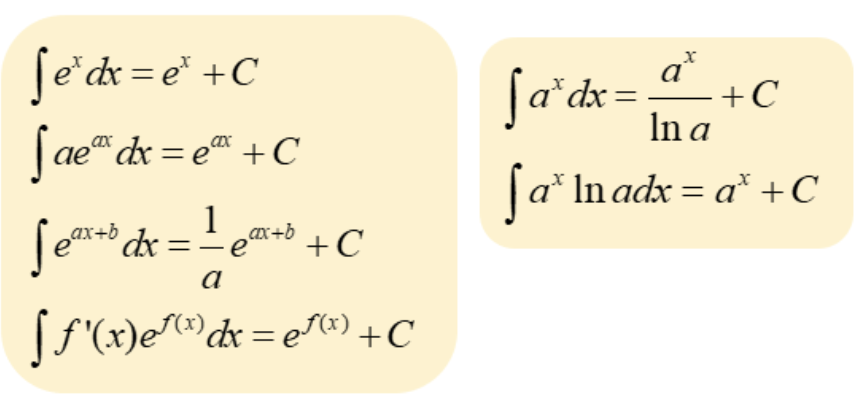
First Fundamental Theorem of Calculus

\int_a^b f'(x) \, dx = f(b) - f(a)

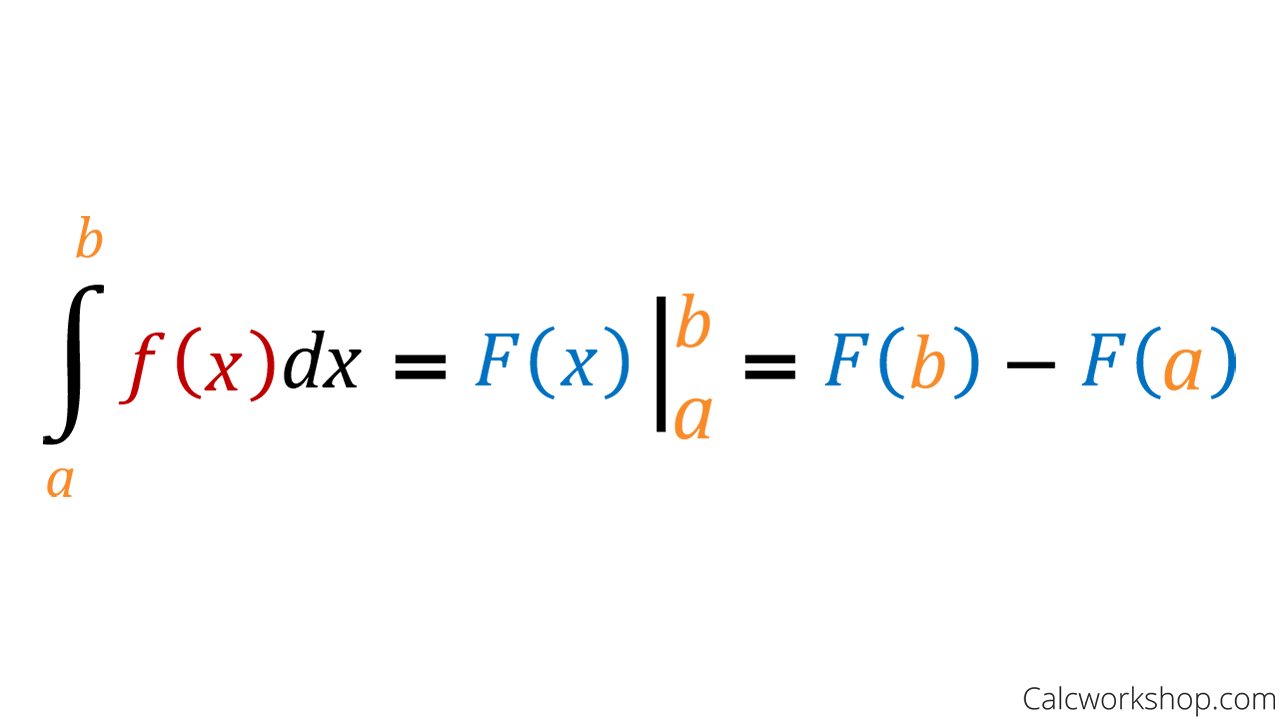
Second Fundamental Theorem of Calculus

d/dx \ int_x^a f(x) \, dx = f(x)

Chain Rule Version of Fundamental Theorem of Calculus

If F is an antiderivative of f and g is differentiable, then \int_{g(a)}^{g(b)} f(t) \, dt = F(g(b)) - F(g(a)) \cdot g'(x).

Average Value of Function on [a, b]

1/(b - a) * \int_a^b f(x) \, dx

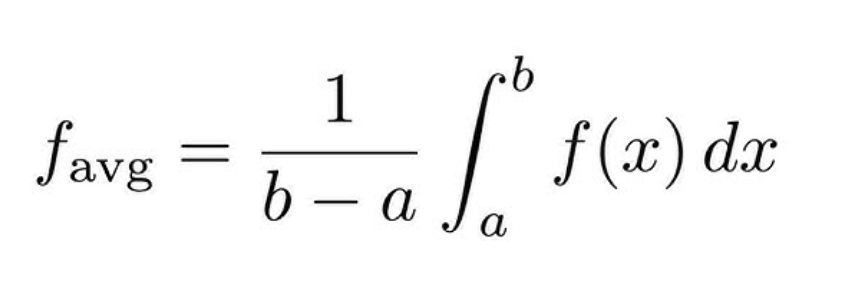
Derivative of arc-trig

d/dx [arcsin(x)] = 1/√(1-x²)

d/dx [arctan(x)] = 1/(1+x²)

d/dx [arcsec(x)] = 1/(|x|√(x²-1))

d/dx [arccos(x)] = -1/√(1-x²)

d/dx [arccot(x)] = -1/(1+x²)

d/dx [arccsc(x)] = -1/(|x|√(x²-1))

Integral of other funny functions

\int \1/√(a² - x²) \, dx = arcsin(x/a) + C

\int \1/√(x² - a²) \, dx = 1/a * arctan(x/a) + C

\int \1/x√(a² - x²) \, dx = 1/a * arcsec(|x|/a) + C

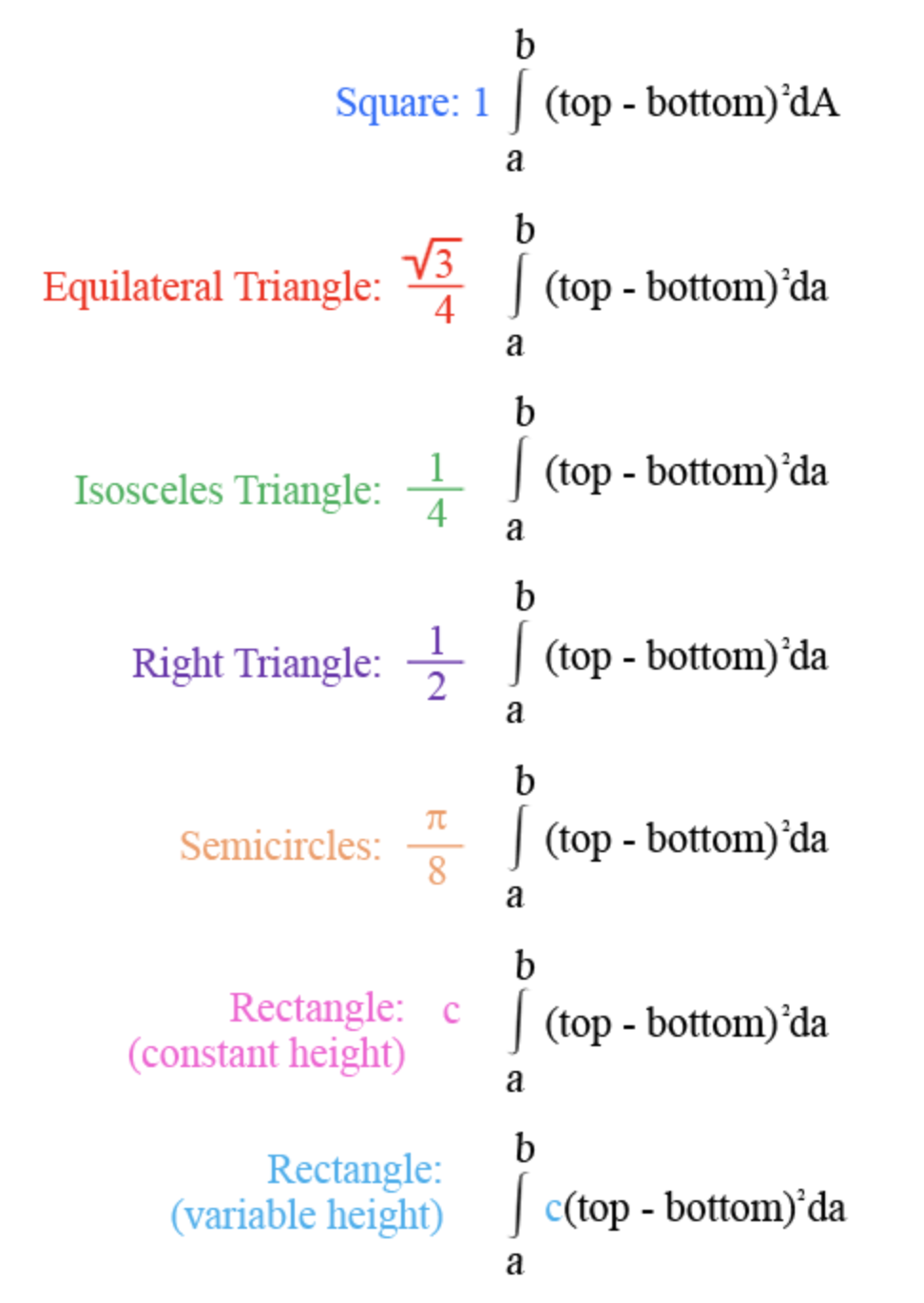
Volume by cross-sections taken perpendicular to the x-acis

V = \int_a^b A(x) \, dx where A(x) is the area of the cross-section

*remember to multiply by various constants based on shape

Volume around x-axis by disc method (no gap)

V = π \int_a^b (r(x))² \, dx

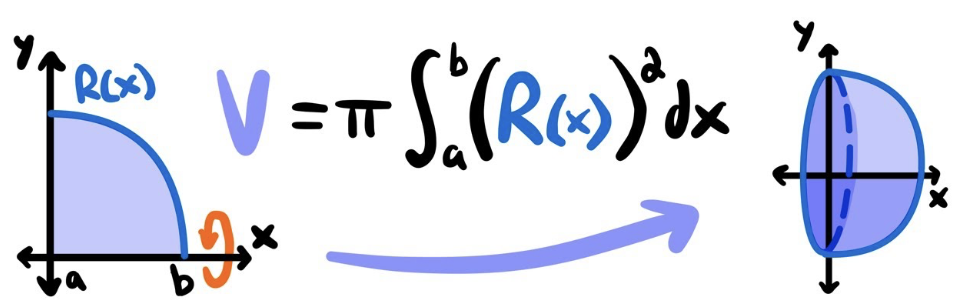
Volume around x-axis by washer method (with gap)

V = π \int_a^b ((R(x))^2 - (r(x))^2) \, dx

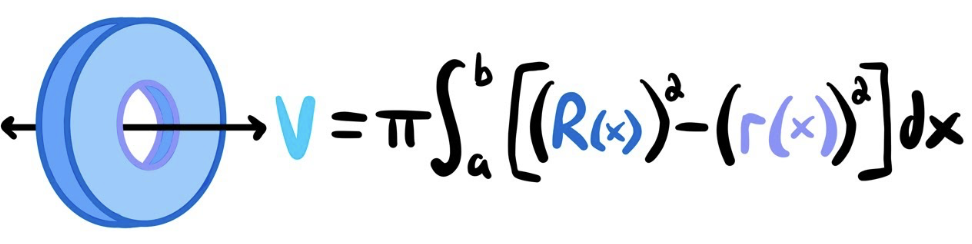
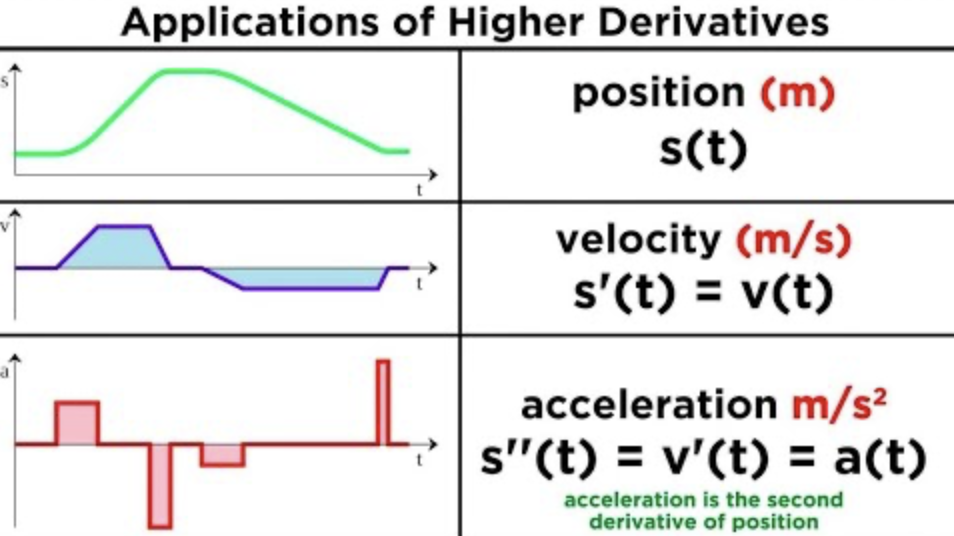
Relation between position = s(t) or sometimes p(t), velocity = v(t), and acceleration = a(t)

derivative of the position function s(t) with respect to time = s’(t), the velocity function v(t), and the derivative of the velocity function v(t) with respect to time = v’(t) is the acceleration function a(t)

Speed

|v(t)|

Displacement (change in position) from x =a to x = b

Displacement = \int_a^b v(t) \, dt

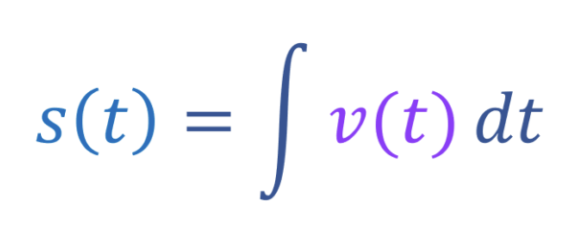
Total Distance travelled from x = a to x = b

Total Distance = \int_a^b |v(t)| \, dt

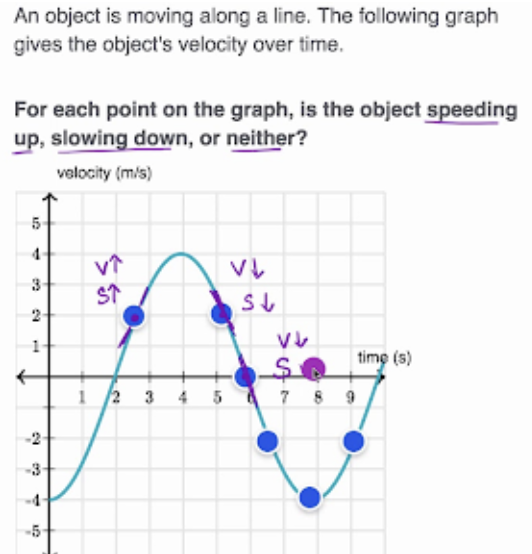
Speed of object is increasing when

velocity and acceleration have the same sign (meaning are in the same direction)

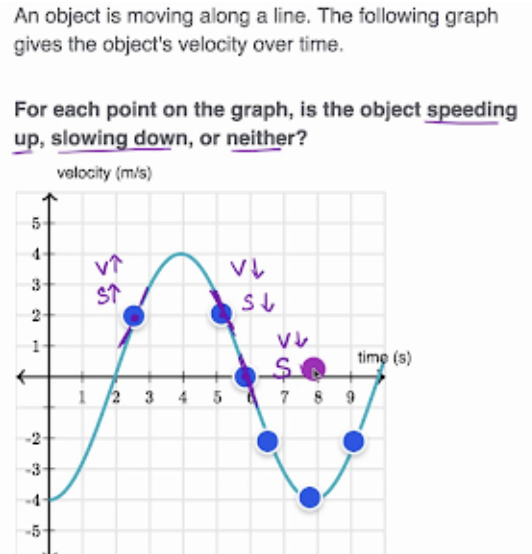
Speed of object is decreasing when

velocity and acceleration have opposite signs (in opposite directions)