pre calc final

y=x parent graph

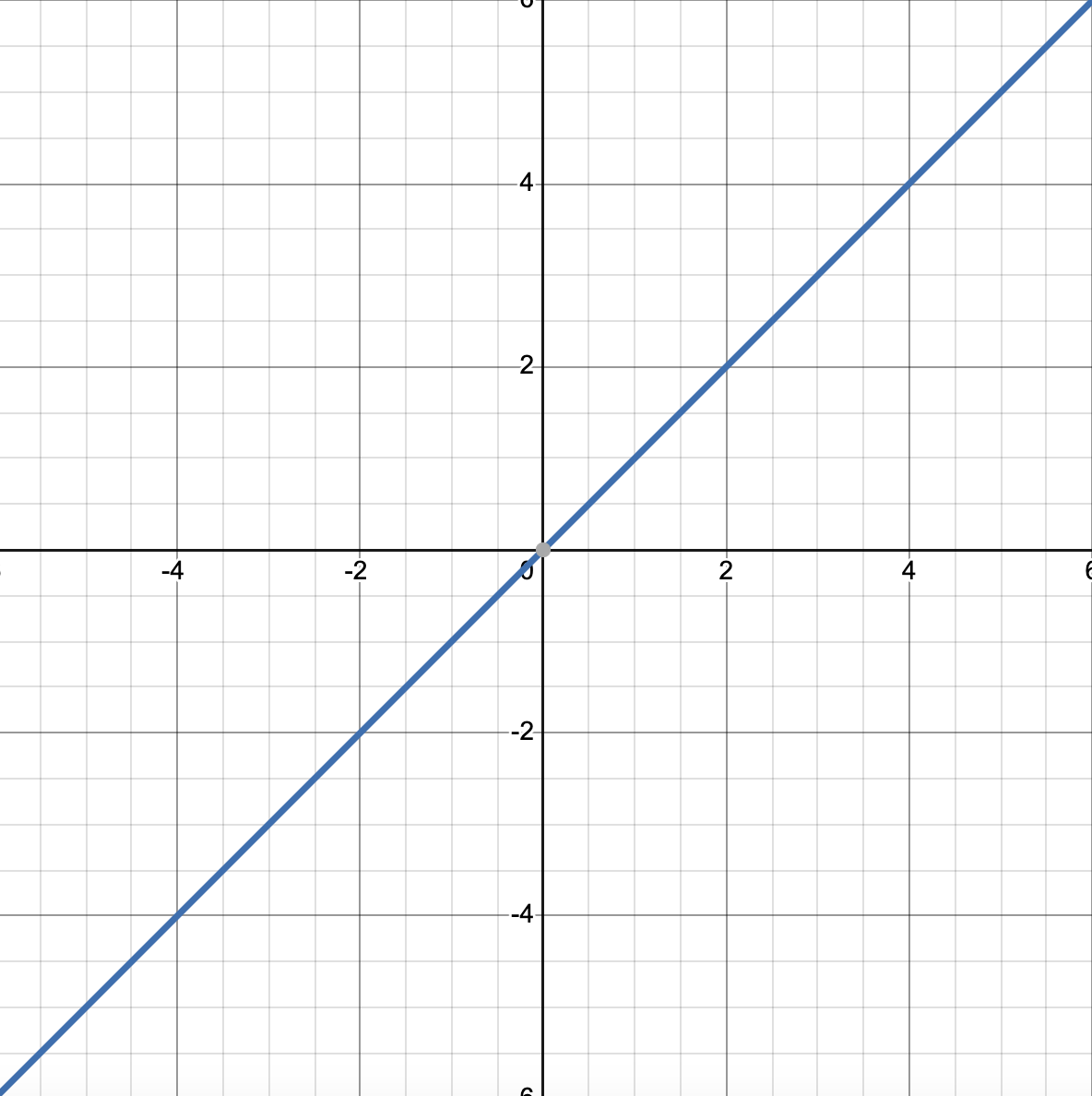
y=x² parent graph

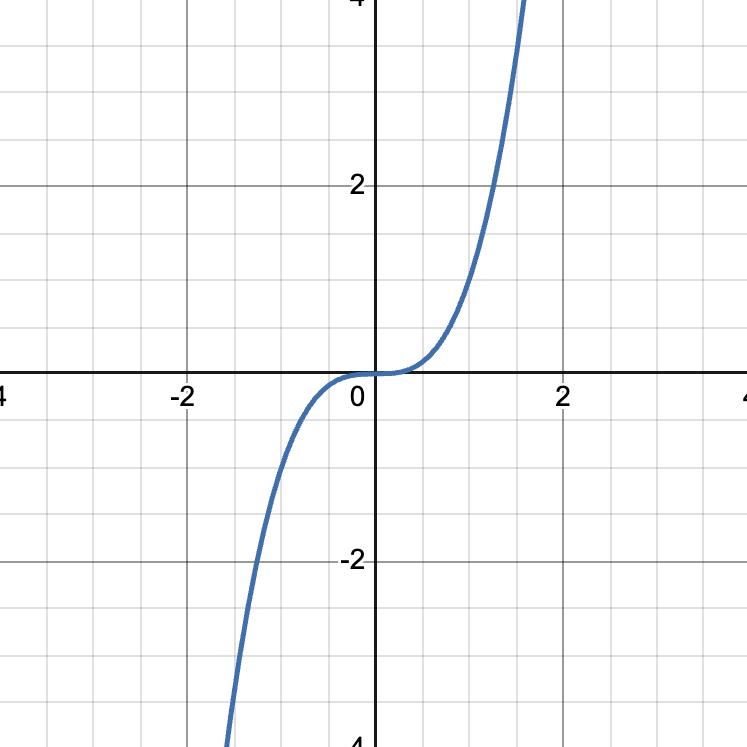
y=x³ parent graph

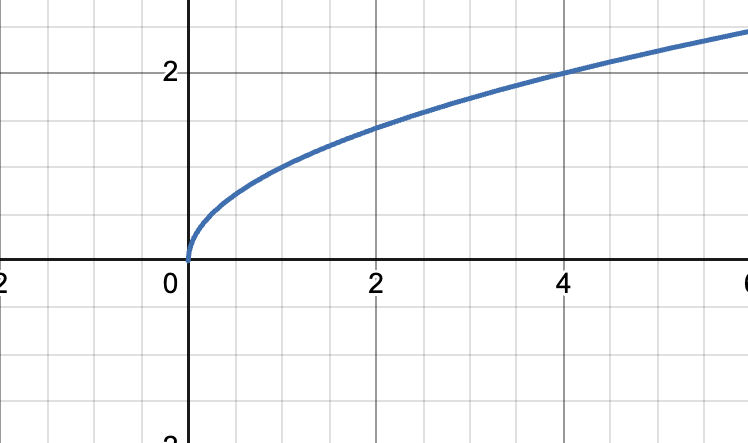
y=sqrt(x) parent graph

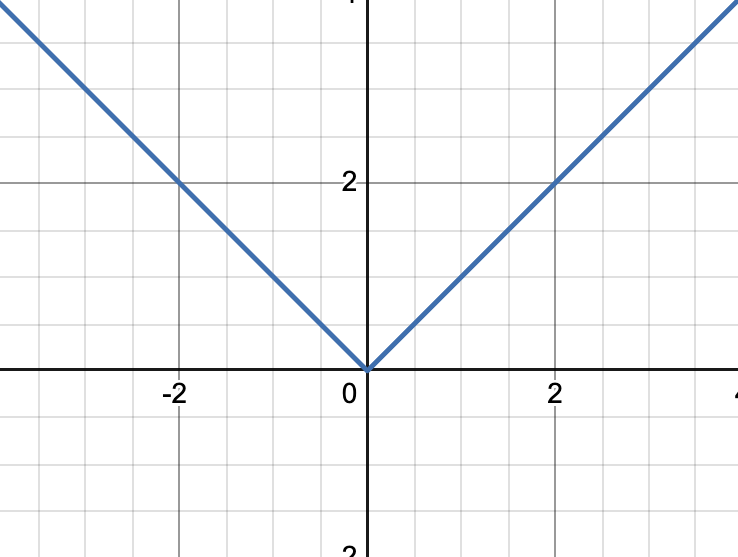
y=|x| parent graph

y=e^x parent graph

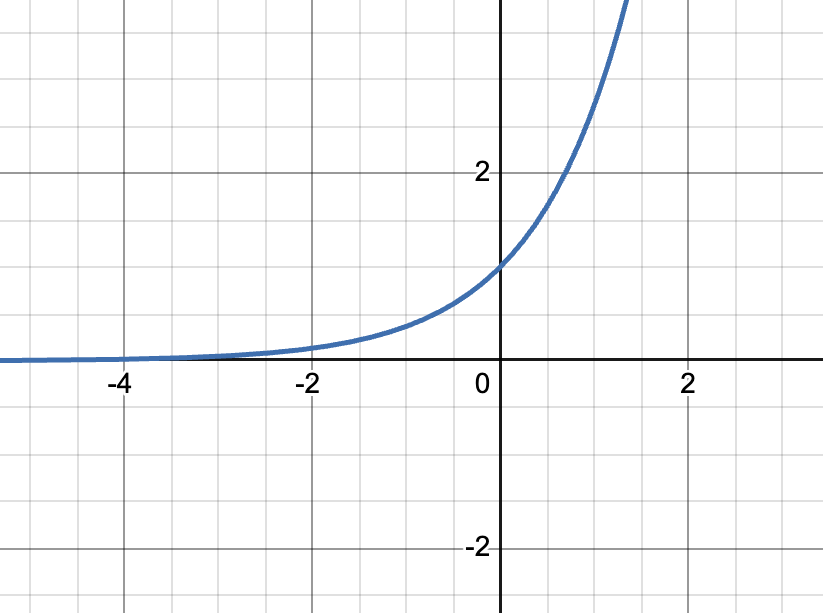
y=lnx parent graoh

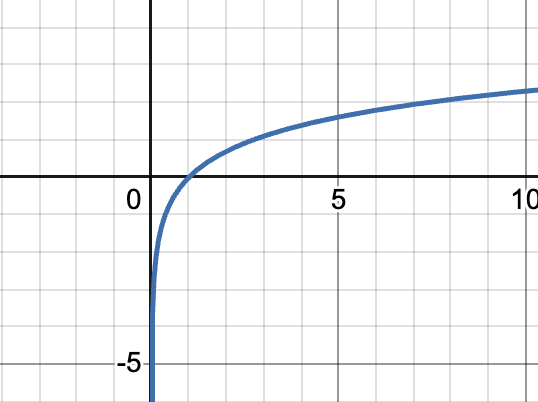
x²+y²=1 parent graph

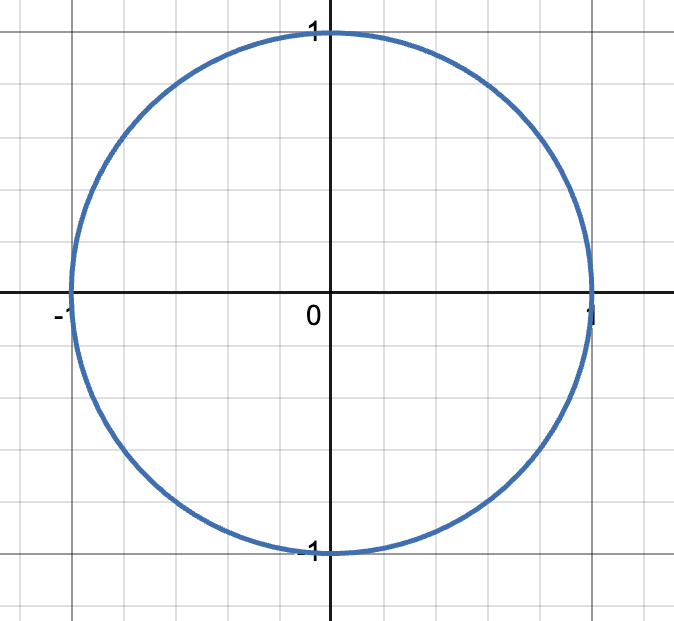
y=1/x parent graph

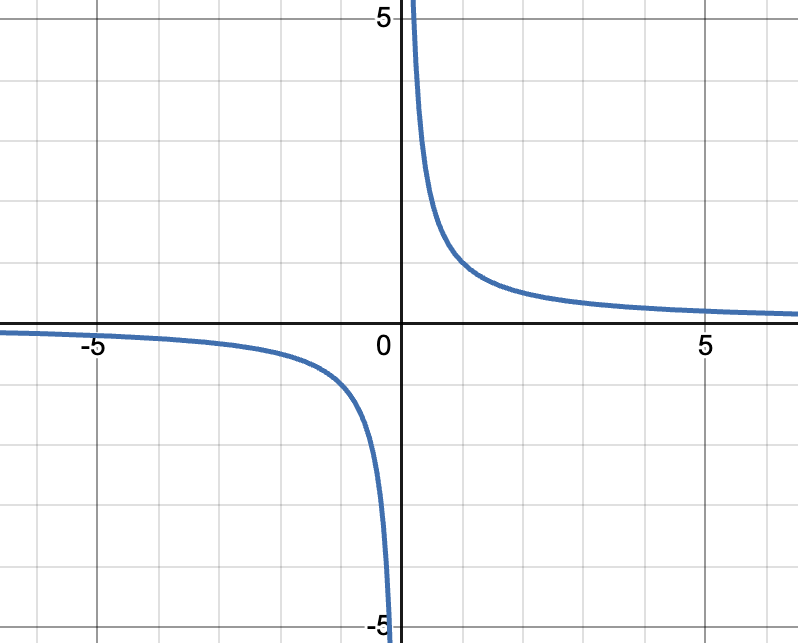
y=sinx parent graph

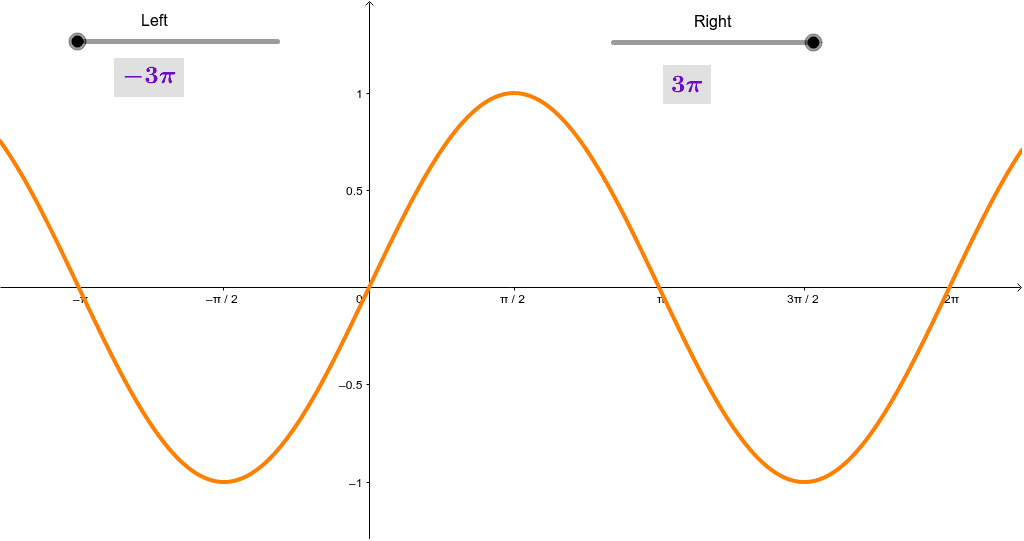
y=cosx parent graph

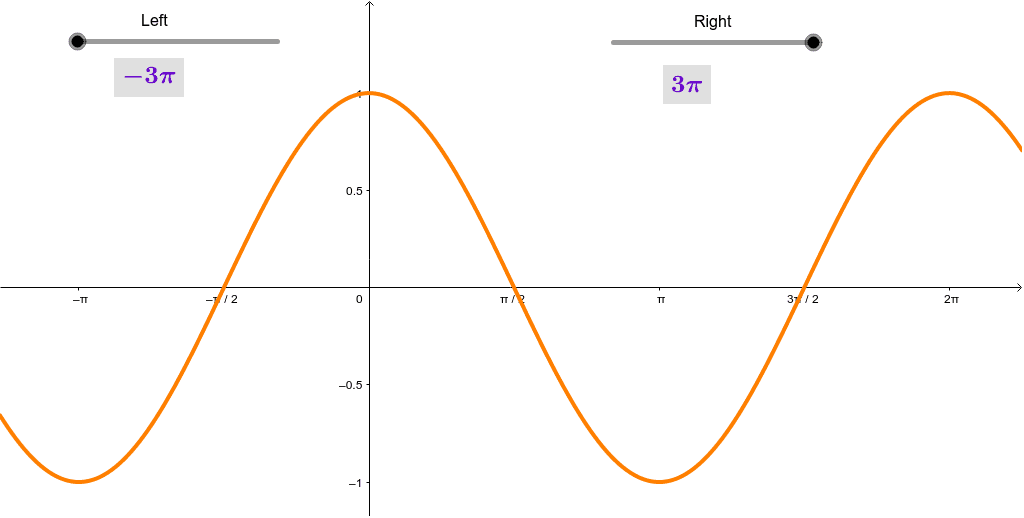
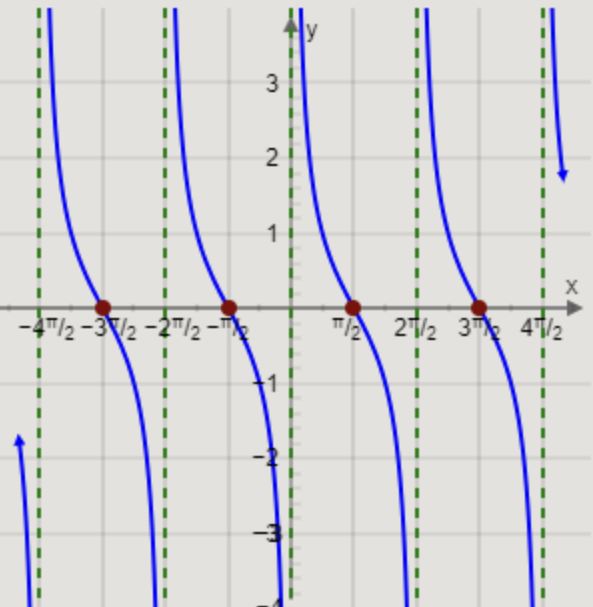
y=tanx parent graph

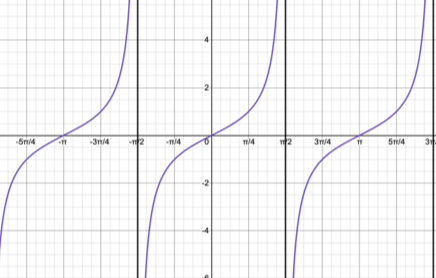
y=cscx parent graph

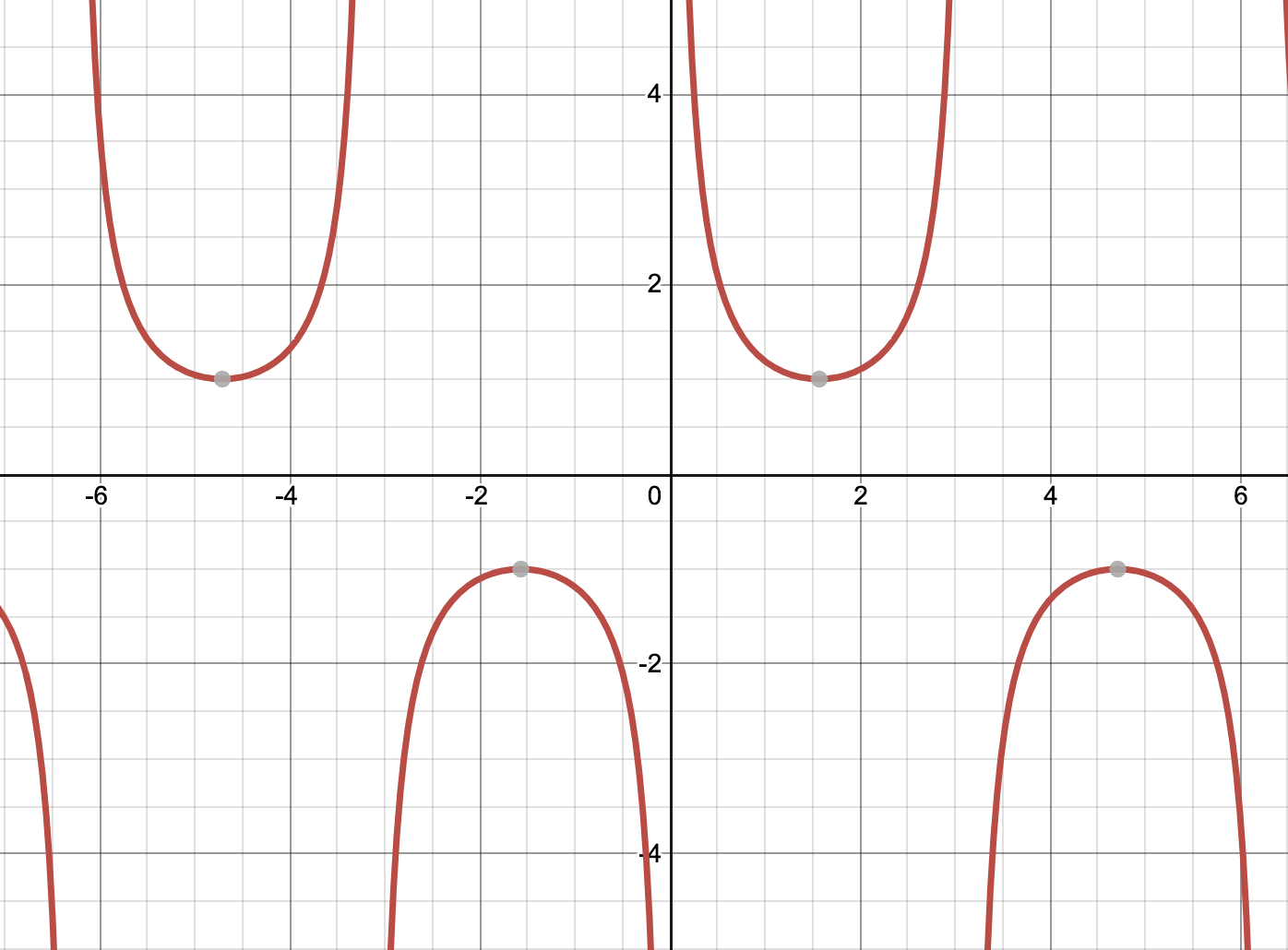
y=secx parent graph

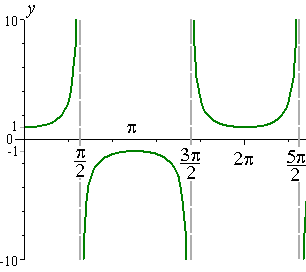
y=cotx parent graph

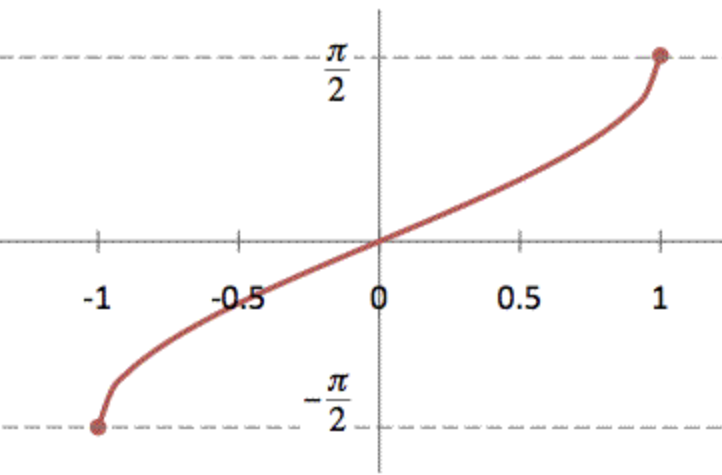
y=arcsinx parent graph

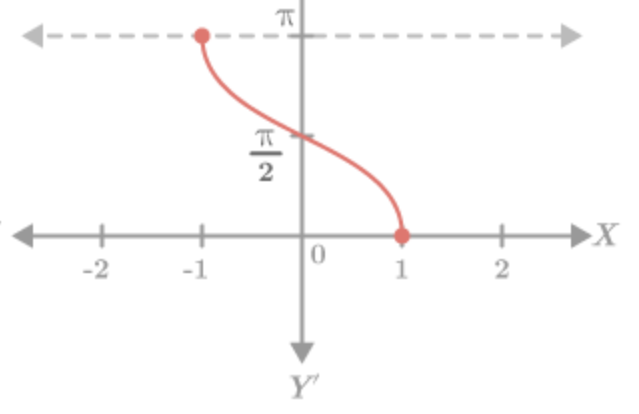
y=arccosx parent graph

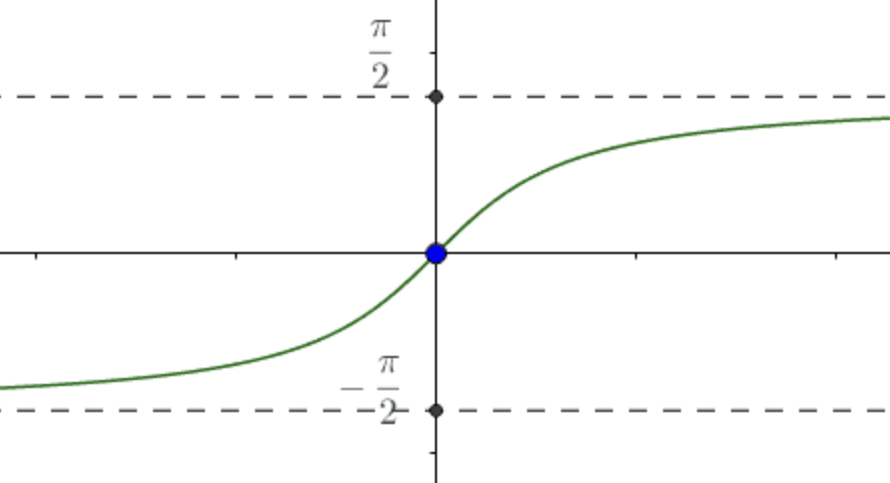
y=arctanx parent graph

even function — graphically

symmetric over y axis

even function — algebraically

f(-x)=f(x)

odd function — graphically

symmetric about the origin

odd function — algebraically

f(-x)=-f(x)

parabola conic formula

(y-k)²=4c(x-h) or (x-h)²=4c(y-k)

vertex/center of conic

(h,k)

what is c in a parabola

distance between vertex and focus

ellipse conic formula

((x-h)²/a²) + ((y-k)²/b²)=1 or ((y-k)²/a²) + ((x-h)²/b²)=1

ellipse pythag formula

b²+c²=a²

ellipse AND hyperbola length of major axis and minor axis

2a, 2b

ellipse AND hyperbola distance between foci

2c

hyperbola conic formula

((x-h)²/a²) - ((y-k)²/b²)=1 or ((y-k)²/a²) - ((x-h)²/b²)=1

hyperbola pythag theorem

b²+a²=c²

eccentricity — parabola

Pf/Pd = 1

eccentricity — ellipse

0 < Pf/Pd < 1

eccentricity — hyperbola

Pf/Pd > 1

intermediate value theorem

If f(x) is continuous on [a, b] then for every y between f(a) and f(b) there exists an x = c between a and b such that f(c) = y

a limit is continuous if…

f(c) exists

lim as x —> c of f(x) exists

lim as x —> c of f(x) = f(c)

remainder theorem

if a polynomial function, f, is divided by (x - a), then the remainder is f(a).

factor theorem

if (x - a) divides a polynomial function, f, evenly, then f(a) = 0

slope of secant line to f(x) on [a,b]

(f(b)-f(a))/(b-a)

slope of tangent line to f(x) at x=c

the derivative and f’(c)=lim as x—>c. of (f(x)-f(c))/(x-c)

exponential functions and logarithmic functions are…

inverses of each other (y=logbaseb(x) ←> b^y=x)

definition of e

e^x = lin as n→infinity of (1+(x/n))^n

compound interest — n times per year

A=P(1+(r/n))^nt

compound interest — continuously

A=Pe^rt

log base b of c =

(log base a of c)/(log base a of b)

log base b of xy =

log base b of x + log base b of y

log base b of x/y =

log base b of x - log base b of y

log base b of x^y=

y*log base b of x

sin(theta) =

y/r

cos(theta)=

x/r

tan(theta)=

y/x

domain and range of y=sinx

D:(-infinity,infinity)

R: [-1,1]

domain and range of y=cosx

D:(-infinity,infinity)

R: [-1,1]

domain and range of y=tanx

D: x=/ (pi/2) + pi*k (k э z)

reciprocal of csc(theta)

1/sin(theta)

reciprocal of sec(theta)

1/cos(theta)

reciprocal of tan(theta)

1/cot(theta)

domain and range of y=arcsinx

D: [-1,1]

R: [(-pi/2),(pi,2)]

domain and range of y=arccosx

D: [-1,1]

R: [0, pi]

domain and range of y=arctanx

D: [-infinity, infinity]

R: ((-pi/2),(pi,2))

SAS area formula

A(triangle) = .5absinC

law of sines

a/sinA = b/sinB = c/sinC

law of cosines

a²=b²+c²-2abcosA

sinusoidal func equation

y=Asin(b(x-c))+D or y=Acos(b(x-c))+D

A in sinusoidal func

amplitude

period in sinusoidal func

2pi/b

c in in sinusoidal func

phase shift

D in sinusoidal func

vertical displacement

pythag IDs

sin²(theta)+cos²(theta)=1

1+cot²(theta)=csc²(theta)

tan²(theta)+1=sec²(theta)

even/odd IDs

sin(-x)=-sinx

cos(-x)=cosx

tan)-x=-tanx

co-function IDs

sin(90-x) = cosx

cos(90-x) = sinx

csc(90-x) = secx

sec(90-x) = cscx

cot(90-x) = tanx

tan(90-x) = cotx

quotient IDs

tanx = sinx/cosx

cotx = cosx/sinx

sin(A+B)=

sinAcosB+cosAsinB

cos(A+B)=

cosAcosB - sinAsinB

tan(A+B)=

(tanA+tanB)/(1-tanAtanB)

complex numbers rect form

x+yi

complex numbers polar/trig form

r*cisx where r>0, 0<x<2pi

magnitude — rectangular

|x+yi| = sqrt(x²+y²)

magnitude — polar

|r*cisx| = r

argument — rectangular

arg(x+yi) = arctan(y/x) or arctan(y/x)+pi

argument — polar

arg(rcis(theta))=theta

multiplication law/ De Moivre’s Theorem

acisa*bcisb = abcis(a+b) / (rcisx)^n = r^n cis(n*pi)

polar coordinates

(r,theta)

converting between rectangular and polar equations

x=rcos(theta)

y=rsin(theta)

tan(theta)=y/x

x²+y²=r²

combinations definition

order does NOT matter, n over k = nCk = n!/((n-k)!k!)

permutations definition

order matters, n!/(n-k)!

n over k is…

the number in row n column k of Pascal’s Triangle where the first row is row zero and the first column is column zero

(n-1 over k) + (n-1 over k+1)

the binomial theorem

(a+b)^n = (n over 0) a^n + (n over 1) n^(n-1)b^1 +…

gicen an arithmetic sequence of a, a+d, a+2d …

an = a1 + (n-1)d

n sigma (k=1) (a1+(k-1)*d) = (a1+an)(n/2)

This is Gauss’ method and instead of using the formula you can just use the fact

(first term + last term) (# of pairs/2)

If you are given a geometric sequence of a1, a1*r, a1*r² …

an = a1*r^(n-1)

n sigma (k=1) (a1*r^(k-1)) = a1(1-r^n)/(1-r)

This is Euclid’s method and you can derive it by multiplying the sum by the common ratio and then subtracting the equations

if |r| < 1 then infinity sigma (k=1) (a1*r^(k-1)) = a1*(1/(1-r))

n sigma (k=1) (k) =

(n(n+1))/2

n sigma (k=1) (k²) =

(n(n+1)(2n+1))/6