1 Working Scientifically

State the meanings of the prefixes: pico, nano, micro, milli, kilo, mega, giga, tera.

Give examples of base quantities and base units, derived quantities and derived units.

Accurate

How close a measured value is to the true value

Precise

How close repeated measurements are to one another

Resolution

The smallest measuring interval on a measuring instrument

Valid

A measurement is valid if it measures what it is supposed to be measuring.

Repeatable

If measurements are repeated by the same person in the same laboratory with the same equipment and the repeated results are close to each other.

Reproducible

If measurements are repeated by a different person or using different techniques and the results are close to each other.

True value

The value that would have been obtained in an ideal measurement.

Uncertainty

The interval within which the true value can be considered to lie with a given level of confidence.

Error

The difference between the measurement result and the true value (not a mistake in the measurement)

A student comments that the measurement of 2.40V is more precise than the measurement of 2.4V. Explain why they are incorrect.

Precision is a measure of the closeness of repeated measurements.

Both 2.40V and 2.4V are single measurements so we cannot comment on their ‘precision’.

The result 2.40V has been measured using a higher resolution multimeter.

So 2.40V has a lower absolute uncertainty (=resolution/2 = 0.005V) compared to 2.4V (absolute uncertainty = 0.1/2 = 0.05V).

Explain why doing repeat measurements increases the likelihood of an accurate measurement.

Repeating measurements reduces the effect of random error.

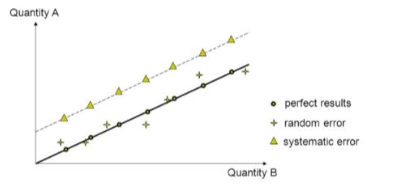
Describe how data with a systematic error would affect the appearance of a line of best fit on a graph

It would adjust the value of the y or x intercept as every data point has the same error

Describe how data with a random error would affect the appearance of a line of best fit on a graph

It would increase the spread of data around the line of best fit - both above and below the line.

Describe how to calculate the absolute uncertainty in a single reading

Absolute uncertainty in a single reading = resolution/2

Describe how to calculate the absolute uncertainty in a set of repeated data eg in the diameter measurement of 66mm, 65mm and 63mm

First exclude anomalies. Then calculate range.

Absolute uncertainty = range/2

State the formula for calculating percentage uncertainty

Percentage uncertainty = (absolute uncertainty/mean value) x100 → if we have repeats.

Percentage uncertainty = (absolute uncertainty/measurement) x100 → if we have a single measurement.

Explain the experimental choices we should make to increase the likelihood of us getting an accurate result.

We should aim to reduce the % uncertainty in the measurements.

To do this we could choose equipment with a high resolution. This will have a low absolute uncertainty, resulting in a low % uncertainty.

Or, where possible, we should increase the measurement we are taking. For the same absolute uncertainty this will reduce the % uncertainty (as % uncertainty = 100 x absolute uncertainty/measurement).

We should also check for 0 error on all instruments and subtract or add any zero error to each measurement.

To determine the acceleration due to gravity, a student drops a ball from an upstairs window instead of a lower one. Explain why this is more likely to produce an accurate result.

The time taken for the ball to fall will increase.

Reducing the % uncertainty in the measurement of time.

Show how to calculate the absolute uncertainty in a measurement when given its percentage uncertainty.

Absolute uncertainty = (percentage uncertainty/100) x mean value.

State the range of values a measured value can take when given its percentage uncertainty, eg if resistance = 4.0Ω ±2% what is the range of resistance?

Calculate the absolute uncertainty first: (2/100) x 4 = 0.08.

So resistance = 4.0±0.08Ω

Or minimum resistance = 3.92Ω and maximum resistance = 4.08Ω

State the equation for % difference and explain what it can tell us about a measurement.

% difference = 100 x (measured value − true value)/true value.

This is a measure of the accuracy of the experiment as it is quantifying the difference between the true value and the measurement.

Describe examples of things that may have caused a result to be inaccurate.

Parallax error introduces random error (if the viewer is looking at the scale from different angles each time) or systematic error (if the viewer is looking at the scale from a consistently wrong angle).

Zero error may have introduced systematic error.

Describe what is meant by 0 error and explain how to correct it

Zero error is a systematic error that occurs when a measuring instrument does not display exactly 0 when no object is being measured.

To correct it you should subtract or add the 0 error.

Explain why a digital thermometer is a better choice of a device than an in glass thermometer to measure temperature.

A digital thermometer will have a higher resolution, leading to a measurement with a lower absolute uncertainty and therefore lower % uncertainty.

A digital thermometer also avoids parallax error.

Describe 5 things to identify when criticising a table of results.

All data in a column should be to the same number of decimal places as the resolution of an instrument.

All data that has been calculated from raw data should be to the same number of significant figures as the raw data.

Repeats should be evident.

The range of the independent variable should be high.

At least 6 sets of results should be taken.

A student carries out an experiment to determine the resistance of a device by measuring the current and pd across it for different values of the current. They produce the following table. Criticise this set of results.

All values of current should be given to the same number of dp.

All values of pd should be given to the same number of dp.

All values of resistance should be given to the same number of sf as the raw data it was calculated from: ie as the pd and current so all resistance values should have 2sf.

There are only 4 sets of results - there should be at least 6.

There is no evidence of repeats.

The range of values of the current is too small.

Define directly proportional and describe its graphical appearance.

Two quantities are directly proportional if when one increases by a certain factor the other increases by the same factor.

It will be a straight line through the origin.

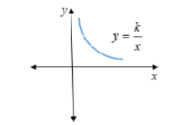
Draw a graph illustrating the relationship between 2 quantities that are inversely proportional.

Explain why we should always seek to plot a striaght line graph in physics.

It is only through converting equations into y=mx+c form and drawing straight line graphs that the validity of equations can be tested and constants determined.

An inverse proportion graph looks very similar to (for example) an inverse square graph - it is difficult to ‘spot’ the relationship when drawing curves.

A student wants to determine the value of the acceleration due to gravity. He measures the time taken for a ball to fall a distance s. He substitutes his measured values into the equation g=2s/t². Another student changes the displacement through which the ball falls, s, and measures the time taken in each case. She plots a graph of t² against s, draws a line of best fit and determines the gradient = 2/g. She calculates g as 2/gradient. Explain which result is likely to be more accurate.

The student who plots a graph is likely to get a more accurate result.

Because the line of best fit averages the results.

This reduces the effect of random error.

Describe, by rearranging the equation into y=mx+c form, what should be plotted on each axis to give a straight line for the following equations.

a) EMF = V + Ir (changing I and measuring V)

b) s = ½ gt² (changing s and measuring t)

c)T = 2π√(l/g) (changing l and measuring T)

d) E = hc/λ (changing λ and measuring E)

e) ρ = RA/l (changing I and measuring R)

All are in form y=mx+c in that order.

a) V = −rI + EMF

b) t² = 2/g x s

c)T² = 4π²/g x l

d) E = hc x 1/λ

e) R = ρ/A x l

Explain why a graph of R against I(length) would produce a straight line graph through the origin.

The equation linking R and I can be rearranged into the form:

R = ρ/A l which is in the form y=mx

Where the gradient is ρ/A. As both ρ and A are constants, the gradient is a constant and so the graph should be a straight line.

The line should pass through the origin as the y-intercept, c, is zero.

Rules for finding total uncertainty in a quantity calculted from the addition of 2 other quantities, eg what is abs uncertainty in A = B + C when B and C have abs uncertainties of ± 0.5mm each?

When combining quantities using addition, always add absolute uncertainties.

The absolute uncertainty in A = 0.5+0.5 = 1.0mm

Rules for finding total uncertainty in a quantity calculated from the multiplication/division of 2 other quantities, eg what is %uncertainty in A=BC²/D⁴ when each B, C and D have %uncertainties of 5%?

When combining uncertainties for quantities that are multiplied or divided, always add the % uncertainties.

When quantity is raised to a power, multiply by the number in the power.

So in this case %U(A) = %U(B) + 2%U(C) + 4%U(D) = 5 + 2×5 + 4×5 = 35%

How to judge if result is accurate or not.

If %dif is less than %unc, result is accurate. (Ensure to compare actual values, not just state the fact).

OR

Determine absolute uncertainty from %u and the value. Then compare true value to the max/min result. eg if true val = 12m, and max value for x = 11m, then result is inaccurate.

OR

If nothing known about the %u, then compare %dif to 5%.