Kin 483-Ch.3: Percentiles

Exam 1

Percentile (definition)

• point or position on a continuous scale of 100 theoretical divisions

  or

• percentage of observations that fall at a given point and below that point

Percentile (example)

• Percentiles are obtained from raw scores

• Sheena did 200lbs (raw score) on a 1 RM squat test

  Is this good or poor?

• We need to evaluate her based on the performance of other competitors

  Sheena is in the 85th percentile

• A percentile score of 85% means Sheena performed equal to or better than 85% of her competitors

Common Percentile Divisions

• Quartiles: Q1 = 0- 25th percentile, Q2 = 25-50th, Q3 = 50-75th, Q4 = 75-100th

• Deciles: same premise as quartiles but divided into 10 parts

• Quintiles: same premise as quartiles but divided into 5 parts

Calculating Percentiles (Rank Order Distributions example)

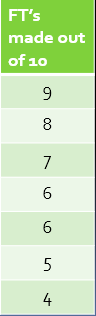
7 basketball players are asked to shoot 10 Free throws

How many scores fall at or below 8 FT’s made?

1) Count the number of scores from 8 down

2) Divide the number of scores you counted by the total players

6/7 = .86

3) Multiply 100

4) 86th percentile

Calculating Percentiles (Simple Frequency Distributions)

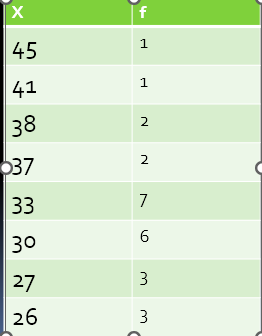
What is the percentile for the athletes with a vertical leap of 33 inches?

1) Add the frequency numbers for raw scores 33 and below

2) Divide the number by the total number of athletes

19/25 = .76

3) Multiply by 100 = 76th percentile

Calculating Percentiles (Grouped Frequency Distributions)

What is the percentile of an athlete who is in the 23 inch vertical leap range?

1) We must assume a normal distribution because we don’t know individual scores within a range

2) P =[(X - L)/ i )] * f + C / N

P = percentile

X = raw score

L = lower limit of interval

i = size of interval

f = frequency of interval

C = cumulative frequency of interval below the

interval in question

N = total number of cases