Finite State Machines, NFA's, DFA's

Finite State Machine

A set of finite states that have actions to go between states. Exists as a graph. A single starting state and can have multiple ending states. Can represent regular expressions and whether an expression is accepted or not.

Needs an alphabet (∑), set of states (Q), start state (q0 ∈ Q), final states (F ⊆ Q),

• DFA Transitions (δ:Q×∑↦Q)

• NFA Transitions (δ:Q×(∑∪{ϵ})↦Q) (NFA contains explicit epsilon transitions)

Regex Requirements

Alphabet:

• Set of symbols allowed

• Denoted by ∑

• A string is a finite sequence of symbols from ∑

Concatenation:

• If L1 and L2 are languages, L1 concatenated with L2 is L1L2

• Allows other characters or strings to be combined

• “a” + “b” = “ab”

Branching (Unions):

• If L1 and L2 are languages, L1 unioned with L2 is L1 U L2

• Therefore, {x | x ∈ L1 V x ∈ L2}

• L1 = {“a”}, L2 = {“b”, … L1 U L2 U … = [a-z]

Repetition (Kleene Closure):

• If L1 is a language, then L1* = {x | x ∈ L1 V x ∈ L1L1 V …}

• If L1 = {“a”}, then L1* = a*

Turing Machine

Can solve any solvable problem.

Regular Languages

Any language created by Regular expressions are regular languages

NFA

A type of finite state that contains explicit epsilon transitions. Easier to make than DFA’s but harder to check regex acceptance. Can have more than one outward edge of the same character.

DFA

A type of NFA that doesn’t contain explicit epsilon transitions. Easy to check acceptance. All DFA’s are NFA’s.

ϵ-closure(state)

Returns a list containing all states that can be reached using epsilon transitions from the current state.

move(state, action)

Returns a list containing all states you can get to using a specific symbol (not counting epsilon transitions between states).

Regex to NFA

Concatenation is just adding an epsilon transition from one machine to another

Branching is adding epsilon transistion to sepaarete branches that go to the same place

Kleene operator is adding an edge back to a previous state to show repetitions

(picture is: (ab|cd)+)

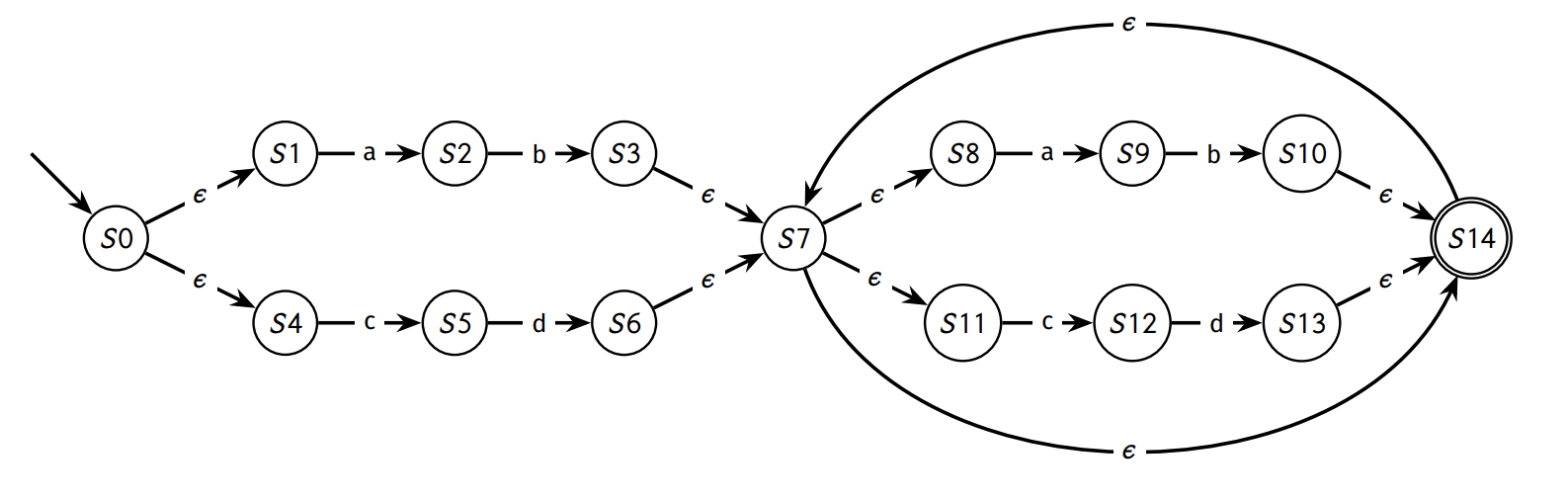
NFA to DFA

Costly to check if an NFA accepts an input or not, so converting after combining several other machines can be good. There can be uncertainty because there can be multiple outgoing edges of the same action, so the goal is to create a new state that represents that uncertainty.