Exponentials and Logarithms (Year 1 - Chapter 14)

Exponential Functions

Functions where the value of y is determined by a constant to the power of x.

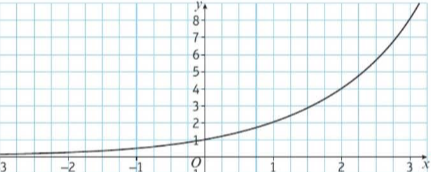
e^x

For all real values of x, the function and gradient function of e^x are identical as e is equal to 2.71828.

Exponential modelling

e^x can be utilised to model situations where rate of growth is proporitonal to the size of what is growing.

Logarithms

The inverse of exponentials, they allow you to ask what power number A must be put to in order to produce number B.

If A^x = B then logA(B)=x.

The Multiplication Law

2 logs of the same base can be added by multiplying their contents together.

loga(X) + loga(Y) = loga(XY).

The Division Law

2 logs of the same base can be subtracted by dividing their contents.

loga(X) - loga(Y) = loga(X/Y).

The Power Law

A log containing a power can be simplified by multiplying the log by the power and removing it from the inside.

loga(X^k) = k x loga(X).

Logs With the Same Base and Contents

Logs of this type always result in 0.

loga(a) = 1.

Logs with Contents of 1

Logs of this type will always give a result of 0.

loga(1) = 0.

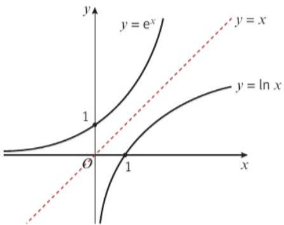
Natural Logarithms

ln represents log with a base of e, it is the inverse of e, thus the graph is inverted.

Non-linear Data

In order to plot a set of exponential data as a straight line graph you can plot the log of y against the log of x.