Lineare Algebra 1

Vocabulary flashcards covering definitions from the Linear Algebra 1 lecture notes.

Fibonacci-Folge (𝑎_𝑛)_𝑛≥0

Definiert durch die Rekursion 𝑎₀ = 0, 𝑎₁ = 1, 𝑎_𝑛 = 𝑎_𝑛−1 + 𝑎_𝑛−2 für 𝑛 ≥ 2

ℱ_𝑎,𝑏

Eine Folge definiert durch die Rekursion 𝑎₀ = 0, 𝑎₁ = 1, 𝑎_𝑛 = 𝑎_𝑛−1 + 𝑎_𝑛−2 für 𝑛 ≥ 2 wobei 𝑎, 𝑏 ∈ ℝ.

V

Die Menge aller Fibonacci-Folgen, d.h. 𝑉 = {ℱ_𝑎,𝑏 ∶ 𝑎, 𝑏 ∈ ℝ}

Summe von ℱ und 𝒢

Definiert als die Folge ℱ + 𝒢 = (𝑎_𝑛 + 𝑏_{𝑛)𝑛≥0,} wobei ℱ = (𝑎_𝑛)_𝑛≥0 und 𝒢 = (𝑏_𝑛)_𝑛≥0 ∈ 𝑉.

Skalarprodukt von ℱ und 𝛼

Definiert als die Folge 𝛼 ∙ ℱ = (𝛼 ∙ 𝑎𝑛)_𝑛≥0, wobei ℱ = (𝑎_𝑛)_𝑛≥0 ∈ 𝑉 und 𝛼 ∈ ℝ.

Vektorraums über ℝ

V hat die Struktur eines Vektorraums über ℝ, wenn für

• ℱ, 𝒢 ∈ 𝑉 gilt ℱ + 𝒢 ∈ 𝑉

• ℱ ∈ 𝑉 und 𝛼 ∈ ℝ gilt 𝛼 ∙ ℱ ∈ 𝑉.

Es gilt…

• ℱ_a,b + ℱ_c,d = ℱ_a+c + ℱ_b+d

• 𝛼 ∙ ℱ_a,b = ℱ_𝛼a,𝛼b

Linearkombination

Die Gleichung schreibt ℱ als eine Linearkombination der Folgen ℱ_1,0 und ℱ_0,1, so dass ℱ = 𝛼 ∙ ℱ_1,0 + 𝛽 ∙ ℱ_0,1

Symmetrie von V

Eine Abbildung 𝑇: 𝑉 → 𝑉 ist eine Symmetrie von V, wenn für alle ℱ, 𝒢 ∈ 𝑉 und 𝛼 ∈ ℝ gilt, dass 𝑇(ℱ + 𝒢) = 𝑇(ℱ) + 𝑇(𝒢) und 𝑇(𝛼 ∙ ℱ) = 𝛼 ∙ 𝑇(ℱ). T ist eine lineare Abbildung.

Verschiebungs-Abbildung 𝑆 ∶ 𝑉 → 𝑉

Definiert als (𝑎₀, 𝑎₁, … ) ↦ (𝑎₁, 𝑎₂, … )

Eigenfolge

Sei 𝑇 ∶ 𝑉 → 𝑉 eine Symmetrie. Eine Folge ℱ ∈ 𝑉, ℱ ≠ ℱ_0,0 ist eine Eigenfolge, wenn es ein Element 𝛼 ∈ ℝ gibt so dass 𝑇(ℱ) = 𝛼 ∙ ℱ. In diesem Fall heisst 𝛼 der Eigenwert der Folge ℱ.

Eigenfolge der Abbildung S

Geschlossene Form der Folgen

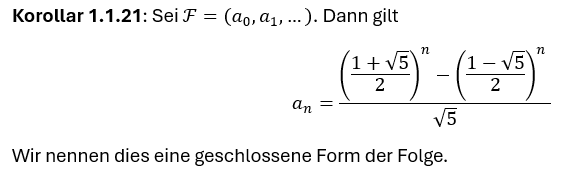
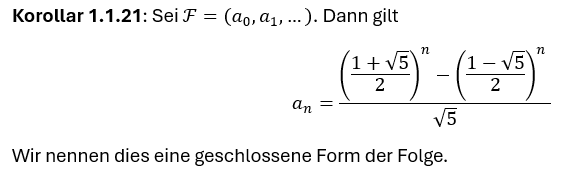
Menge

Eine Sammlung von Objekten. Die Objekte heissen die Elemente dieser Menge.

𝑥 ∈ 𝑀

y /∈ M

x ist ein Element von M.

y ist kein Element von M.

Regeln der Mengen

• Reihenfolg speilt keine Rolle

• Wiederholungen werden ignoriert

• Mengen können Elemente von Mengen sein

• Eine Menge muss nicht umbedingt Elemente der gleichen Art enthalten.

𝑀 = {𝑥 ∶ 𝐴(𝑥)} oder {𝑥 | 𝐴(𝑥)}

Die Menge aller x mit einer bestimmen Eigenschaft A(x).

𝑃 ⊆ 𝑄

P ist eine Unter- oder Teilmenge von Q, wenn für alle 𝑥 ∈ 𝑃 gilt: 𝑥 ∈ 𝑄.

𝑃 ⊊ 𝑄

P ist eine strikte Unter- oder Teilmenge von Q, wenn 𝑃 ⊆ 𝑄 und 𝑃 ≠ 𝑄.

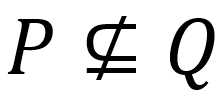
P keine Teilmenge von Q

𝑃 ∩ 𝑄

Die Schnittmenge von P und Q, definiert als {𝑥| 𝑥 ∈ 𝑃 und 𝑥 ∈ 𝑄}

• Elemente die sowohl in P und in Q sind

𝑃 ∪ 𝑄

Die Vereinigungsmenge von P und Q, definiert als {𝑥| 𝑥 ∈ 𝑃 oder 𝑥 ∈ 𝑄}

• Elemente die in P oder in Q sind

𝑃 − 𝑄

P ohne Q, definiert als {𝑥| 𝑥 ∈ 𝑃 und 𝑥 ∉ 𝑄}

• Elemente die nur in P sind.

𝑄^𝑐

Das Komplement von Q (in P)

• wenn Q eine Teilmenge von P ist, dann nennen wir P ohne Q das Komplement von Q (in P)

Cartesisches Produkt von X und Y

Die Menge aller geordneten Paare (𝑥, 𝑦) mit 𝑥 ∈ 𝑋 und 𝑦 ∈ 𝑌: 𝑋 × 𝑌 = {(𝑥, 𝑦) ∶ 𝑥 ∈ 𝑋, 𝑦 ∈ 𝑌}

Das ist einfach die Menge aller möglichen geordneten Paare, bei denen das erste Element aus X kommt und das zweite aus Y.

n-fache Cartesische Produkt von X

Die Menge 𝑋^𝑛 = {(𝑥₁, … , 𝑥_𝑛) ∶ 𝑥₁, … , 𝑥_𝑛 ∈ 𝑋}

Für eine Menge X ist das n-fache kartesische Produkt Xⁿ die Menge aller n-Tupel, also geordneter Listen mit nnn Einträgen aus X.

Funktion (oder Abbildung) 𝑓: 𝑋 → 𝑌

Eine Relation, die jedem Element 𝑥 ∈ 𝑋 genau ein Element 𝑓(𝑥) ∈ 𝑌 zuordnet; wir schreiben 𝑥 ↦ 𝑓(𝑥).

𝑋 ist die Definitionsmenge und 𝑌 die Zielmenge.

Gleiche Funktionen

Zwei Funktionen  f : X → Y und g : X’ → Y’ sind genau gleich, wenn X = X’ , Y = Y’ und f (x) = g (x) für alle 𝑥 ∈ 𝑋 .

Beschränkung von f auf A

Die Funktion 𝑓|_𝐴 ∶ 𝐴 → 𝑌, 𝑓|_𝐴(𝑥) = 𝑓(𝑥) 𝑓ü𝑟 𝑥 ∈ 𝐴, wobei 𝐴 ⊆ 𝑋.

Injektiv

𝑓 ist Injektiv, wenn für alle 𝑥₁, 𝑥₂ ∈ 𝑋 mit 𝑥₁ ≠ 𝑥₂ 𝑔𝑖𝑙𝑡 𝑓(𝑥₁) ≠ 𝑓(𝑥₂).

• Verschiedene Eingaben ergeben verschiedene Ausgaben.

• Gleiche Eingaben ergeben gleiche Ausgaben

Surjektiv

𝑓 ist surjektiv, wenn für alle 𝑦 ∈ 𝑌 es mindestens ein 𝑥 ∈ 𝑋 gibt, so dass 𝑓(𝑥) = 𝑦.

• Jeder Wert in Y wird mindestens einmal getroffen.

Bijektiv

𝑓 ist bijektiv, wenn f Injektiv und surjektiv ist; mit anderen Worten, für alle 𝑦 ∈ 𝑌 gibt es genau ein 𝑥 ∈ 𝑋, so dass 𝑓(𝑥) = 𝑦.

• Perfekte Zuordnung: Jeder y hat genau ein x

Inverse Funktion 𝑓_⁻¹:𝑌 → 𝑋

Die Funktion, die einem Element 𝑦 ∈ 𝑌 das eindeutig bestimmte Elemente 𝑥 ∈ 𝑋 zuordnet, für das gilt 𝑓(𝑥) = 𝑦, wenn 𝑓: 𝑋 → 𝑌 bijektiv ist.

Funktionskomposition und Reihenfolge

Gegeben seien zwei Funktionen f:X→Y und g:Y→Z. Dann ist die Komposition g∘f definiert und bildet x∈X auf g(f(x))∈Z ab. Die umgekehrte Komposition f∘g ist nur dann definiert, wenn Z = X gilt.

Selbst wenn beide Kompositionen möglich sind, gilt im Allgemeinen:

f∘g ≠ g∘f

Das bedeutet, dass die Reihenfolge der Funktionsauswertung wichtig ist – die Funktionskomposition ist nicht kommutativ.

Eigenschaften von Funktionskompositionen

Seien f:X→Y und g:Y→Zzwei Funktionen. Dann gelten folgende Aussagen über die Komposition g∘f:

1. Wenn sowohl f als auch g injektiv sind, dann ist auch g∘f injektiv.

2. Wenn sowohl f als auch g surjektiv sind, dann ist auch g∘f surjektiv.

3. Wenn sowohl f als auch g bijektiv sind, dann ist auch g∘f bijektiv.

Diese Aussagen zeigen, dass Injektivität, Surjektivität und Bijektivität beim Zusammensetzen von Funktionen erhalten bleiben – wenn beide Funktionen diese Eigenschaft besitzen.

Körper

Eine Menge 𝐾 ≠ ∅ mit zwei Abbildungen

+∶ 𝐾 × 𝐾 → 𝐾 (Addition) und

∙ ∶ 𝐾 × 𝐾 → 𝐾 (Multiplikation)

und zwei ausgezeichneten Elementen 0, 1 ∈ 𝐾 mit 0 ≠ 1, die bestimmte Eigenschaften erfüllen

𝔽_𝑝

Der Körper definiert als die Elemente {0, . . . , 𝑝 − 1} für eine Primzahl p. Für 𝑥, 𝑦 ∈ 𝔽_𝑝 definieren wir 𝑥 + 𝑦 ∈ 𝔽_𝑝 (bzw. 𝑥𝑦 ∈ 𝔽_𝑝) als den Rest, der bei der Division durch p entsteht.

• Ist ein Körper

• Schwierigkeit zu zeigen: Existenz eines multiplikativen inversen

Multiplikatives Inverse von 𝔽_𝑝

Sei x∈𝔽_𝑝 ein von null verschiedenes Element. Dann existiert ein y∈𝔽_𝑝​, sodass gilt:

x⋅y=1

Man nennt dieses y das multiplikative Inverse von x und schreibt:

y=x⁻¹

Das bedeutet: In jedem endlichen Körper 𝔽_𝑝​ (mit p Primzahl) hat jedes x≠0 ein Inverses bezüglich der Multiplikation.

Die Menge 𝔽_𝑝^×= 𝔽_𝑝∖{0} ist also eine Gruppe unter der Multiplikation.

Kommutativer Ring

Eine Menge ℝ mit Operationen + und ·, die alle Axiome aus Definition 2.1.1 ausser 8 erfüllen.

Ebenso ist die Menge der Reste, die bei Division durch n entstehen, ein kommutativer Ring, der genau dann  ein Körper ist, wenn n eine Primzahl ist

(𝑚 × 𝑛) Matrix A

Eine Tabelle mit m Zeilen und n Spalten, deren Einträgen Elemente von K sind.

Zeilenvektor

Eine (1 × 𝑛) Matrix.

Spaltenvektor

Eine (𝑚 × 1) Matrix.

Nullmatrix

Die Nullmatrix 0_m×n​ ist die m×n-Matrix, in der alle Einträge gleich Null sind. Sie wird als:

0_m×n

notiert.

Einheitsmatrix

Die Einheitsmatrix 1_n​ ist die quadratische n×n-Matrix, bei der auf der Diagonalen alle Einträge gleich 1 sind, und alle anderen Einträge gleich 0.

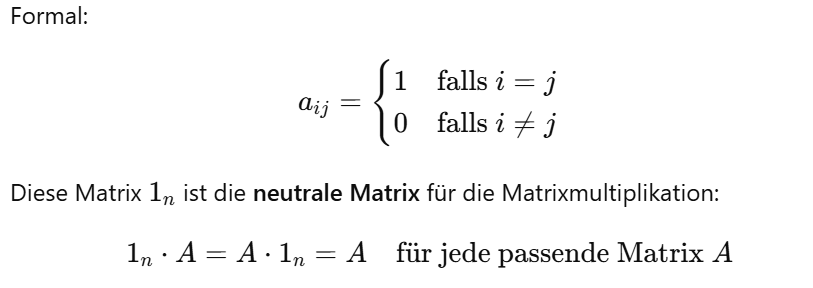
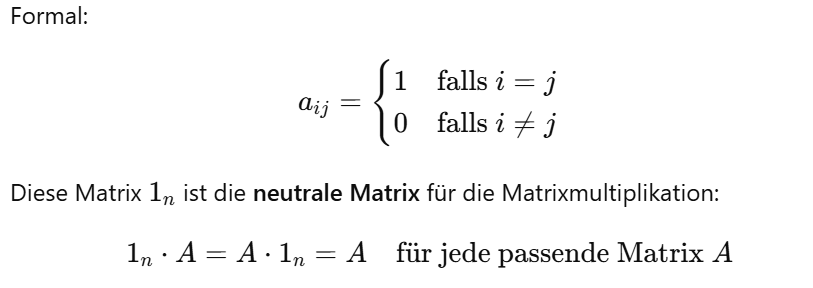
Summe 𝐴 + 𝐵

Die (𝑚 × 𝑛) Matrix (𝑐_𝑖𝑗) mit 𝑐_𝑖𝑗 = 𝑎_𝑖𝑗 + 𝑏_𝑖𝑗, wobei 𝐴 = (𝑎_𝑖𝑗) und 𝐵 = (𝑏_𝑖𝑗) Elemente von 𝑀_𝑚×𝑛(𝐾) sind.

Skalarprodukt 𝛼 ∙ 𝐴

Die Matrix mit Einträgen (𝛼𝑎_𝑖𝑗), wobei 𝐴 = (𝑎_𝑖𝑗) ∈ 𝑀_𝑚×𝑛(𝐾) und 𝛼 ∈ 𝐾.

Rechenregeln für Matrizen

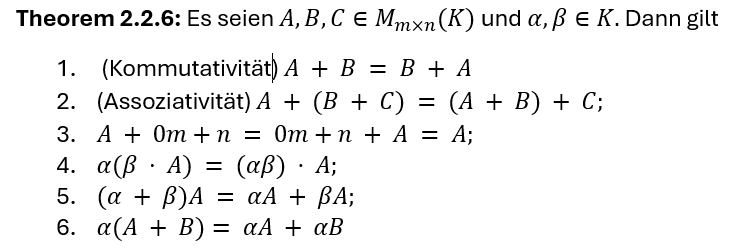
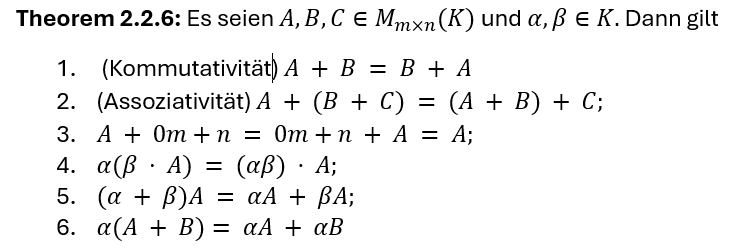
Produkt 𝐴𝐵

Die (𝑚 × 𝑝)-Matrix 𝐶 = (𝑐_𝑖𝑘) mit 𝑐_𝑖𝑘 = ∑𝑎_𝑖𝑗𝑏_𝑗𝑘, wobei 𝐴 ∈ 𝑀_𝑚×𝑛(𝐾) und 𝐵 ∈ 𝑀_𝑛×𝑝(𝐾).

Beachte: Die beiden Produkte AB und BA sind dann und nur dann definiert, wenn n = p. In diesem Fall ist  AB ∈ 𝑀_m×m(𝐾) und BA ∈ 𝑀_n×n(𝐾)                       

Rechenregeln für Matrixmultiplikation

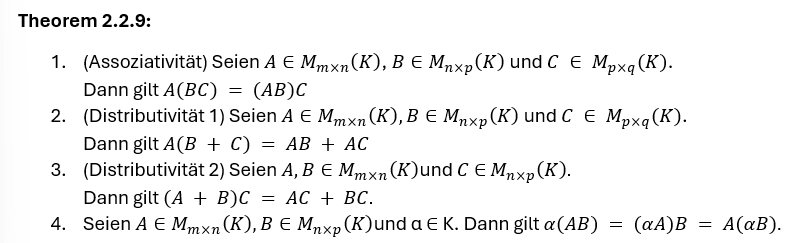
Kommutierende Matrizen

Zwei Matrizen A,B ∈ M_n×n(K) kommutieren, wenn gilt:

AB=BA

Diagonale Matrix

Eine Matrix 𝐴 = (𝑎_𝑖𝑗) ∈ 𝑀_𝑛×𝑛(𝐾), falls (𝑎_𝑖𝑗) = 0 für alle 𝑖 ≠ 𝑗.

Obere Dreiecksmatrix

Eine Matrix 𝐴 = (𝑎_𝑖𝑗) ∈ 𝑀_𝑛×𝑛(𝐾), falls (𝑎_𝑖𝑗) = 0 für alle 𝑖 > 𝑗.

Untere Dreiecksmatrix

Eine Matrix 𝐴 = (𝑎_𝑖𝑗) ∈ 𝑀_𝑛×𝑛(𝐾), falls (𝑎_𝑖𝑗) = 0 für alle 𝑖 < 𝑗.

Invertierbare Matrix

Eine (𝑛 × 𝑛)-Matrix 𝐴 ∈ 𝑀_𝑛×𝑛(𝐾) ist invertierbar, wenn es eine (𝑛 × 𝑛)-Matrix 𝐵 ∈ 𝑀_𝑛×𝑛(𝐾) gibt, so dass 𝐴𝐵 = 𝐵𝐴 = 1_𝑛.

Diese Matrix B nennt man die inverse Matrix von A, und man schreibt sie als:

A⁻¹

Die Inverse ist also eindeutig bestimmt – es kann nur eine Matrix B geben, die A genau „rückgängig“ macht.

Inverse eines Matrixprodukts

Seien A und B zwei invertierbare n×n-Matrizen. Dann gilt für das Produkt AB:

(AB)⁻¹=B⁻¹A⁻¹

Die Reihenfolge kehrt sich beim invertieren um

Elementare Zeilenumformungen (EZU)

Operationen auf eine (𝑚 × 𝑛)-Matrix 𝐴:

• 𝑃(𝑟, 𝑠): Vertauschen der Zeilen r und s;

• 𝑀(𝑟, 𝜆): Multiplikation der Zeile r mit λ;

• 𝑆(𝑟, 𝑠, 𝜆): Addition von 𝜆 × (Zeile 𝑟) zur Zeile s.

Zeilen-äquivalent

Zwei Matrizen 𝐴 und 𝐴⁻¹ sind zeilen-äquivalent, wenn wir 𝐴⁻¹ durch die Anwendung von endlich vielen (EZU)s auf A erhalten.

Jede Matrix ist zeilen-äquivalent zu einer Matrix in reduzierter Zeilenstufenform.

Reduzierte Zeilenstufenform RZSF

Eine (𝑚 × 𝑛) Matrix A ist in reduzierter Zeilenstufenform, wenn:

1. 𝐴 ist in reduzierter Zeilenform;

2. alle Nullzeilen liegen unter den nicht-Nullzeilen;

3. die führende 1 einer Zeile liegt rechts von der führenden 1 der Zeile darüber.

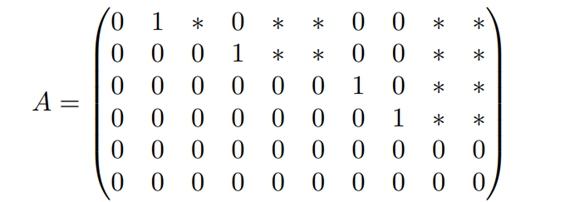
Lineares Gleichungssystem

Ein System von 𝑚 Gleichungen mit 𝑛 Unbekannten 𝑥𝑗, ausgedrückt in Matrizenform als 𝐴𝑥 = 𝑏.

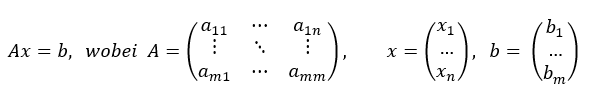
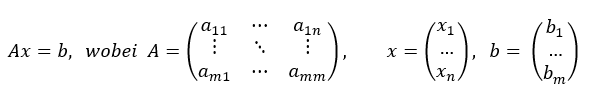
𝐿(𝑆)

Die Lösungen des Gleichungssystems

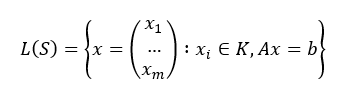
Das lineare Gleichungssystem Ax = b ist durch die erweiterte Matrix  A|_b vollständig bestimmt.

Wenn b=0, dann schreiben wir A anstatt der erweiterten Matix A|₀.

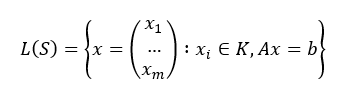
Erweiterte Matrix 𝐴|𝑏

Die (𝑚 × (𝑛 + 1))-Matrix, bei der der Spaltenvektor 𝑏 als (𝑛 + 1)ste Spalte der Matrix A hinzugefügt wird.

Homogenes lineares Gleichungssystem

Ein lineares Gleichungssystem der Form 𝐴𝑥 = 0.

Zeilenäquivalente Gleichungssysteme

Gegeben seien zwei lineare Gleichungssysteme:

• (S):Ax=b(S)

• (S′):A′x=b′(S')

mit jeweils m Gleichungen in n Unbekannten.

Wenn die erweiterten Matrizen A′∣_b′ und A∣_b zeilenäquivalent sind (d. h. durch elementare Zeilenumformungen ineinander überführbar), dann haben die Systeme denselben Lösungsraum:

L(S′)=L(S)

Das bedeutet: Zeilenumformungen verändern die Lösungsmenge eines LGS nicht.

Lösbarkeitsfall eines LGS abhängig von Bedingung

• Fall 1:

  Wenn b₃−b₂+2b₁≠0 dann ist das System nicht lösbar: L(S)=∅

• Fall 2:

  Wenn

  b₃−b₂+2b₁=0

  dann besitzt das System eine Lösungsmenge, die durch freie Variablen beschrieben ist:

  

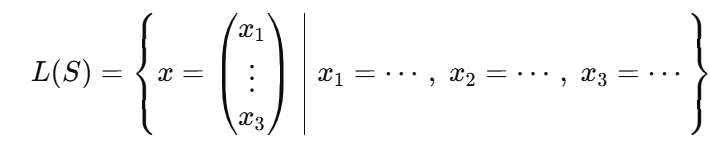
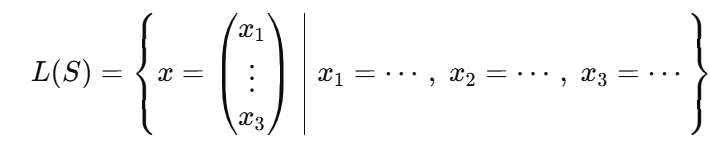
Vektorraum über 𝐾

Eine Menge 𝑉 mit zwei Operationen

+∶ 𝑉 × 𝑉 → 𝑉

×∶ 𝐾 × 𝑉 → 𝑉,

die bestimmte Bedingungen erfüllen:

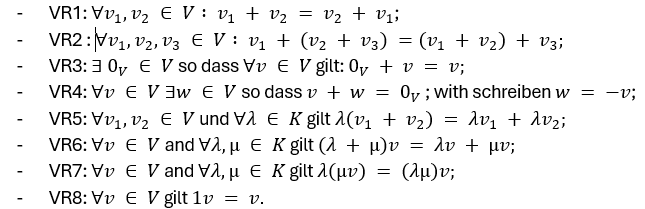
VR3: Es gibt genau ein Element mit der Eigenschaft (VR3), wir nennen es die additive Identität von V.

VR4: Das Element ist in (VR4) eindeutig bestimmt, es heisst das (additive) Inverse von .

VR6: Vektor Addition

VR7: Skalar-Multiplikation

Rechenregeln im Vektorraum mit Nullvektor

Unterraum

Eine Teillmenge 𝑈 ⊆ 𝑉 ist ein Unterraum, wenn 𝑈 ≠ ∅ und wenn sie bezueglich Addition und Skalar-Multiplikation abgeschlossen ist

Also:

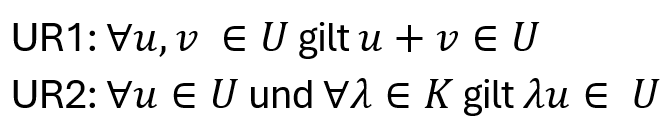
Wir schreiben U ≤ V.

Kriterium für Unterräume: U≤V

Lineare Hülle

Der von 𝑣1, . . . , 𝑣𝑛 erzeugten Unterraum, 〈𝑣1, … , 𝑣𝑛〉 = {𝜆1𝑣1 + ⋯ + 𝜆𝑛𝑣𝑛 ∶ 𝜆𝑖 ∈ 𝐾 ∀1 ≤ 𝑖 ≤ 𝑛}

Linearkombination von 𝑣1, … , 𝑣𝑛

Ein Element der Form 𝜆1𝑣1 + ⋯ + 𝜆𝑛𝑣𝑛 mit 𝜆𝑖 ∈ 𝐾.

Endlich-dimensional

V ist endlich-dimensional, wenn es endlich viele Vektoren 𝑣1, … , 𝑣𝑛 ∈ 𝑉 gibt so dass 𝑉 = 〈𝑣1, … , 𝑣𝑛〉

Erzeugendessystem

𝑣1, … , 𝑣𝑛 ∈ 𝑉 wenn 𝑉 = 〈𝑣1, … , 𝑣𝑛〉

Linear unabhängig

𝑣1, … , 𝑣𝑛 ∈ 𝑉 sind linear unabhängig, wenn sich 0𝑉 eindeutig als Linearkombination dieser Vektor darstellen lässt, nämlich 0𝑉 = 0𝑒1 + ⋯ + 0𝑣𝑛

Basis von V

Ein linear unabhängiges Erzeugenden System von V.

Dimension von V

Die Anzahl von Elementen einer Basis von V; wir schreiben dim𝐾 𝑉.

Komplement von U

Ein Unterraum 𝑊 ≤ 𝑉 ist ein Komplement zu U wenn 𝑉 = 𝑈 + 𝑊 und 𝑈 ∩ 𝑊 = {0}.

Lineare Abbildung

Eine Funktion 𝑇 ∶ 𝑉 → 𝑊 zwischen Vektorräume über K, die folgende Bedingungen erfüllt: 1. 𝑇(𝑣1 + 𝑣2) = 𝑇(𝑣1) + 𝑇(𝑣2) für alle 𝑣1, 𝑣2 ∈ 𝑉 ; 2. 𝑇(𝛼𝑣) = 𝛼 𝑇(𝑣) für all 𝑣 ∈ 𝑉 , 𝛼 ∈ 𝐾.

Endomorphismus

Eine lineare Abbildung 𝑇 ∶ 𝑉 → 𝑉

Kern von T

ker(𝑇) = {𝑣 ∈ 𝑉 ∶ 𝑇(𝑣) = 0𝑤} ⊆ 𝑉

Bild von T

𝑖𝑚(𝑇) = {𝑇(𝑣) ∶ 𝑣 ∈ 𝑉} ⊆ 𝑊

Rang von T

Der Rang 𝑟𝑘(𝑇) von T ist dim𝐾 𝑖𝑚(𝑇).

Isomorphismus

Eine lineare Abbildung 𝑇 ∶ 𝑉 → 𝑊, wenn es eine lineare Abbildung 𝑆 ∶ 𝑊 → 𝑉 gibt, so dass 𝑆 ◦ 𝑇 = 𝑖𝑑𝑉 und 𝑇 ◦ 𝑆 = 𝑖𝑑𝑊

Abbildungsmatrix von T bezüglich der Basen B und C

Die Matrix [𝑇]𝐶 𝐵 = (𝑎𝑖𝑗 ) ∈ 𝑀𝑚×𝑛(𝐾), deren Einträge definiert sind durch 𝑇(𝑣𝑗) = ∑𝑎𝑖𝑗𝑤𝑖

Basiswechselmatrix

Die Matrix 𝐴 = [𝑖𝑑]𝐵′ 𝐵, deren Eintraege definiert sind durch die Gleichungen 𝑣𝑗 = ∑𝑎𝑖𝑗𝑣𝑖 ′

Ähnliche Matrizen

Zwei Matrizen 𝐴, 𝐵 ∈ 𝑀𝑛 × 𝑛(𝐾) sind ähnlich, wenn es eine invertierbare Matrix 𝑃 ∈ 𝑀𝑛×𝑛(𝐾) gibt, so dass 𝐵 = 𝑃−1 · 𝐴 · 𝑃.

Äquivalente Matrizen

Zwei Matrizen 𝐴, 𝐵 ∈ 𝑀𝑚×𝑛(𝐾) sind äquivalent, wenn es invertierbare Matrizen 𝑃 ∈ 𝑀𝑚×𝑚(𝐾) 𝑢𝑛𝑑 𝑄 ∈ 𝑀𝑛×𝑛(𝐾) gibt, so dass 𝐵 = 𝑃 · 𝐴 · 𝑄.

Koordinaten

Die Einträge des Vektors (𝛼1 … 𝛼𝑛) ∈ 𝐾𝑛, wenn 𝑢 = 𝛼1𝑣1 + · · · + 𝛼𝑛𝑣𝑛

Zeilenrang(A)

dim𝐾 𝑍𝑒𝑖𝑙𝑒𝑛(𝐴), wobei 𝑍𝑒𝑖𝑙𝑒𝑛(𝐴) = 〈𝑢1, … , 𝑢𝑚〉 ≤ 𝐾𝑛 die Zeilen von A sind.

Spaltenrang(A)

dim𝐾 𝑆𝑝𝑎𝑙𝑡𝑒𝑛(𝐴), wobei 𝑆𝑝𝑎𝑙𝑡𝑒𝑛(𝐴) = 〈𝑣1, … , 𝑣𝑛〉 ≤ 𝐾𝑚 die Spalten von A sind.

Rang(A)

Der gemeinsame Wert von Zeilen- und Spaltenrang von A.

Transponierte Matrix 𝐵𝑡

Die (𝑛 × 𝑚) − Matrix, deren (𝑖,𝑗) Eintrag durch 𝑏𝑗𝑖 gegeben ist.

Gruppe

Eine Menge G zusammen mit einer Operation ⋆∶ 𝐺 × 𝐺 → 𝐺, die Assoziativität, Existenz eines neutralen Elements und Existenz eines Inversen erfüllt.

Ring

Eine Menge R mit zwei Operationen + (Addition) und × (Multiplikation), die (R, +) als eine abelsche Gruppe, assoziative Multiplikation, ein Element 1𝑅 ∈ 𝑅 für das gilt 1𝑅 × 𝑎 = 𝑎 × 1𝑅 = 𝑎 und distributive Multiplikation bezüglich der Addition erfüllt.

Linearformen

Elemente von 𝑉∗, lineare Abbildungen 𝑉 → 𝐾.

Duale Basis

Die Basis 𝐵∗ = (𝑣1 ∗ , . . . , 𝑣𝑛 ∗), wobei 𝑣𝑖 ∗ ∈ 𝑉∗ wie folgt definiert ist: 𝑣𝑖 ∗ (𝑣𝑗 ) = {1 𝑤𝑒𝑛𝑛 𝑖 = 𝑗 0 𝑤𝑒𝑛𝑛 𝑖 ≠ 𝑗.

Duale Abbildung

𝑇∗ ∶ 𝑊∗ → 𝑉∗ , ℓ ↦ ℓ ◦ 𝑇

Annulator von 𝑈

Die 𝑀enge aller Linearformen von V , die alle Elemente von 𝑈 auf Null abbilden, das heisst 𝑈∘ = {ℓ ∈ 𝑉∗ ∶ ℓ(𝑢) = 0𝑉 ∀ 𝑢 ∈ 𝑈}.

Bidualraum

Der K-Vektorraum 𝑉∗∗ = (𝑉∗)∗

Kommutatives Diagramm

Ein Diagramm, wobei 𝜏𝑉, 𝜏𝑊 mit T kompatibel sind.

Quotientenraum

Die Elemente von 𝑉/𝑈 sind die Nebenklassen von 𝑈 in 𝑉, die Addition und Skalarmultiplikation sind definiert durch [𝑣1] + [𝑣2] = [𝑣1 + 𝑣2] und 𝛼[𝑣] = [𝛼𝑣].