GW Blok 6 Seminar 1.2 Descriptive statistics for two continuous variables

What is a pearson correlation and how do you calculate it?

• The Pearson correlation coefficient (often denoted as r) measures the strength and direction of the linear relationship between two continuous variables.

• r depends on the average distance of the observations from some straight line

• Value range: -1 to +1

  • +1: Perfect positive linear correlation (as one variable increases, the other increases)

  • -1: Perfect negative linear correlation (as one variable increases, the other decreases)

  • 0: No linear correlation

• Pearson correlation measures linear relationships only

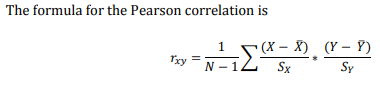
When is it appropriate to calculate the piersons correlation?

• Both variables are continuous and measured on an interval or ratio scale.
  (e.g., height, weight, temperature, test scores)

• The relationship between the two variables is linear.
  Pearson’s correlation measures linear associations — if the relationship is curved or non-linear, Pearson’s r might be misleading.

• Data is approximately normally distributed (especially important for small samples).
  Normality helps with hypothesis testing related to Pearson’s r, though for large samples this assumption is less strict.

• No extreme outliers in either variable.
  Outliers can heavily distort the correlation coefficient.

• Plaatje: 1 en 3 mag je Pierson meten, 2 geen lineair verband en 4 je hebt geen spreiding op x-as

How do you interpret a positive and negative slope in a scatterplot in terms of correlation?

• A positive slope indicates a positive correlation; as X increases, Y also increases.

• A negative slope indicates a negative correlation; as X increases, Y decreases

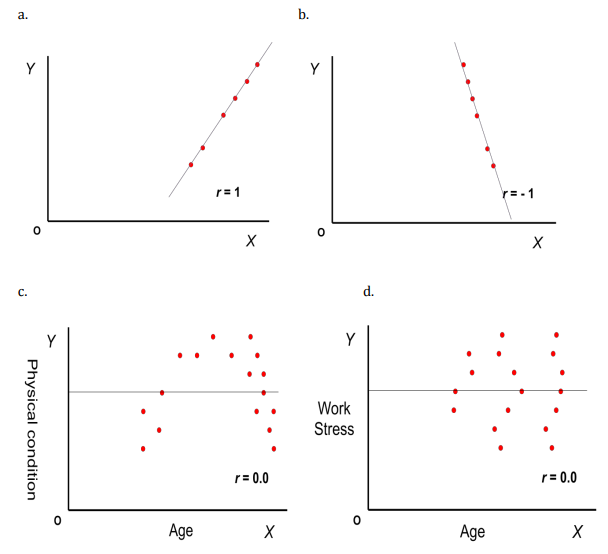
Interpret the following graphs

Perfect positive relationship (Figure 1.7 a)

• Large X-values are associated with large Y-values.

• The relationship is perfect because if you know the value of X (or Y), then the value of Y (or X) is fully determined. All observations are on a straight line.

• r = 1

Perfect negative relationship (Figure 1.7 b)

• Large X-values are associated with small Y-values.

• This relationship is also perfect and Y (or X) is fully determined by X (or Y).

• In that case the correlation is equal to the optimal negative correlation, i.e. r = -1

Non-linear relationship (Figure 1.7 c)

• In Figure 1.7 c, there is a bell-shaped relationship between X and Y but the Pearson correlation is still equal to 0.

• However, it doesn’t imply no association; it only reflects a zero linear association. There is, however, a quadratic association, which is not a topic of this course.

No association at all (Figure 1.7 d)

• Figure 1.7 d. shows a scatter plot where there is no association at all.

• The way how the Yvalues vary around the horizontal line seems to be unaffected by the value of X, i.e. there is a same amount of variation of Y-values around the horizontal line, independently of the Xvalues.

How is the "quality of fit" of the regression line related to correlation strength?

• The better the fit (less scatter around the line), the stronger the correlation.

• What?

  • Coefficient of determination (R 2 ): 0 ≤ 𝑅^2 ≤ 1

• Why?

  • How good the fitted model is? Or how precise the predicted value is?

• How?

• i.e., how much total variability in the y values (SST) is in the explained part (SSR)

• Interpretation: It indicates the percentage of variability of y explained by the variable x

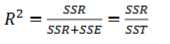
When is it appropriate to use simple linear regression?

• Y variable (dependent variable): quantitative (continuous)

• X variable (independent variable): usually numeric/continuous, but can be categorical

• Goal: determing the (approximately) average Y value for a given X value (or conditional on X).

• X: independent variable/cause

• Y: dependent variable/effect

What is the difference between correlation and regression?

• Correlation coefficient (r):

  • Measures the strength and direction of a linear association between X and Y.

  • Symmetric: correlation of X with Y equals correlation of Y with X.

  • Does not imply causation or prediction.

• Regression:

  • Asymmetric: regression of Y on X is different from regression of X on Y.

  • Focuses on predicting mean Y given X or estimating how Y changes as X changes.

What is the simple linear regression model?

• The general idea of performing a linear regression analysis in our example is to summarize the scatter plot by means of a straight line that can be interpreted as (approximate) average values of length for different values of Age.

• Goals:

  • Effect Size Model: Estimate and interpret effect of X on Y

  • Prediction Model: Predict Y value given X value

How can you calculate B1 and B0?

What is a regression line?

• The best-fitting line minimizes the sum of squared residuals (Method of Least Squares).

• The regression line passes through the point (Xˉ,Yˉ) (the means of X and Y).

• The points on the regression line are only approximately equal to the average Y values, which will be assumed to be equal for very large sample sizes (almost equal to the population size).

• For a finite sample size (which will be the case in practice), these points will be called predicted Y-value and denoted as Y-hat

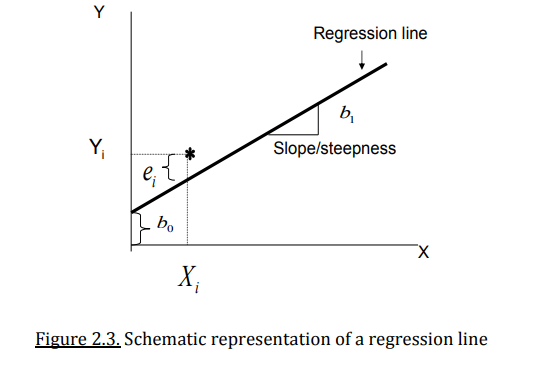
What are residuals?

• The (vertical) deviations of the observation from the line are called the residuals. Reflects how good the regression line summarizes the scatter point by means of a straight line.

• Residuals = observed Y - predicted Y

• They represent unexplained variability due to biological variation, measurement error, or other factors.

• Residuals can be positive (above line) or negative (below line).

• Error: theoretical error

• Residual: observed error for a set of data

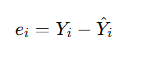
What does the correlation coefficient describe?

It describes only the direction and strength of the association between two variables, not the effect of X on Y or the ability to estimate Y from X.

What is the "method of least squares" in regression?

• It is a method that estimates the best-fitting line by minimizing the sum of squared errors (residuals).

• SSxx: sum of squares for X

  • s2 = variance

• SSyy: sum of squares for Y

• SPxy: sum of product

  • cov = covariance

• The residuals sum to 0

• The line passes through (Xˉ,Yˉ)

How can you visually inspect a scatter plot?

• Think about:

  • Direction

  • Functional form

  • Strength

  • Unusual features

• WHY do we need to investigate these four elements?

  • Because they justify whether Pearson correlation or linear regression model is appropriate!!!

Direction of a scatter plot

• Positive association: the values of y tend to increase as the values of x increase

  • e.g.: Earnings increases by age

• Negative association: the values of y tend to decrease as the values of x increase

  • e.g.: Max legibility distance of highway signs decreases by driver age

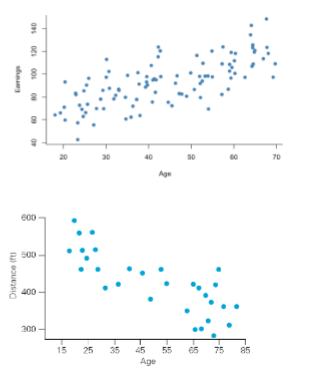
Functional form of a scatter plot

Non-linear vs linear

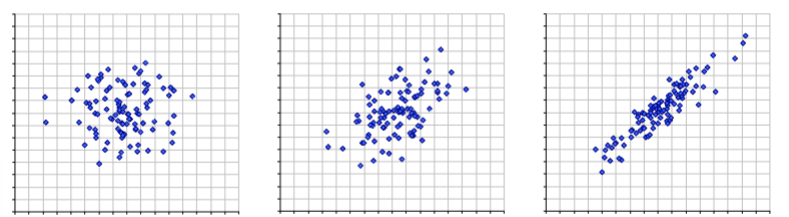
Strength of a scatter plot

• How strong is the association? How strong is the association?

• From weak to highly associated (more straight line)

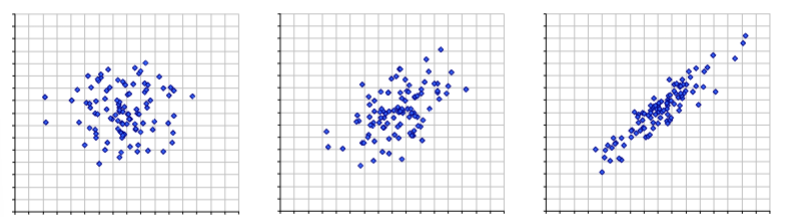
Unusual features of a scatter plot

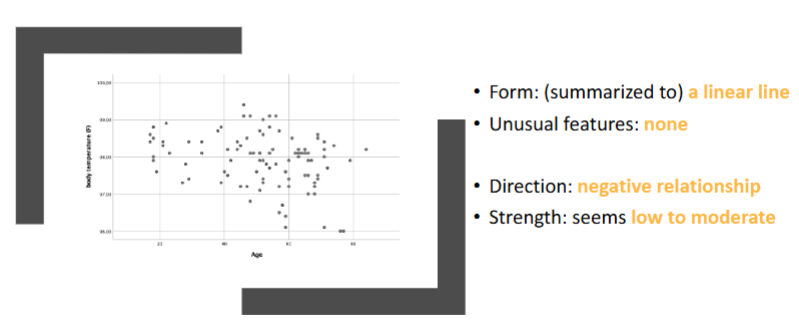
Example inspection scatter plot

What is R squared (R²) and how do you calculate it?

• R2 tells us how well the regression line fits the data.

• It quantifies how much of the variation in the dependent variable (y) is explained by the independent variable (x) using the regression model.

  • 0 ≤ R² ≤ 1

• R² =1 → perfect prediction (all actual values lie on the regression line)

• R² =0 → regression line explains none of the variability in y

• SSR + SSE = SST

NOT A TOPIC OF THIS COURSE What is standard error of the estimate (SEE) and how do you calculate it?

• Measures the average distance between the actual y-values and the predicted y-values.

• It's like a standard deviation of the residuals.

• SEE gives us an absolute measure of prediction error (in units of y).

• Lower SEE means the model predicts more accurately.

NOT A TOPIC OF THIS COURSE What is the difference between R² and SEE

Sum of squares error