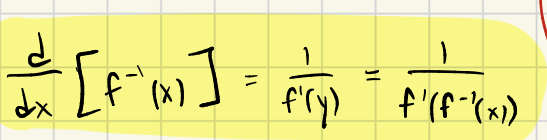Calc AB Unit 2 - Derivatives

Equation for slope of tangent line

m_tan = Lim_h→0 [f(a+h) - f(a)]/h

Derivative equation

f’(x) = Lim_h→0 [f(x+h) - f(x)]/h

d/dx[c] =

Derivative of a constant

0

d/dx[x] =

Derivative of x

1

d/dx[xⁿ] =

Derivative of xⁿ

nx^n-1

d/dx[f(x) ± g(x)] =

Derivative of f(x) ± g(x)

f’(x) ± g’(x)

d/dx[c * f(x)] = 

Derivative of constant times f(x)

c * f’(x)

d/dx[sinx] =

Derivative of sinx

cosx

d/dx[cosx] =

Derivative of cosx

-sinx

d/dx[tanx] =

Derivative of tamnx

sec²x

d/dx[cotx] =

Derivative of cotx

-csc²x

d/dx[secx] =

Derivative of secx

secxtanx

d/dx[lnx] =

Derivative of lnx

1/x 

d/dx[e^x] =

Derivative of e^x

e^x

d/dx[a^x] =

Derivative of a^x

a^x * lna

d/dx[sin^-1x] =

Derivative of sin^-1x

1/√(1-x²)

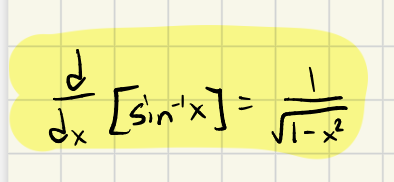
d/dx[cos^-1x] =

Derivative of cos^-1x

-1/√(1-x²)

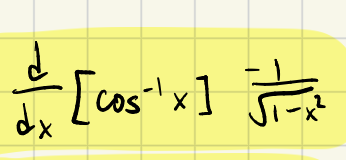
d/dx[tan^-1x] =

Derivative of tan^-1x

1/(1+x²)

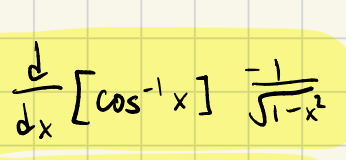
d/dx[f^-1(x)] =

Derivative of f^-1(x)

1/f’(y) 

1/(f’(f^-1(x))