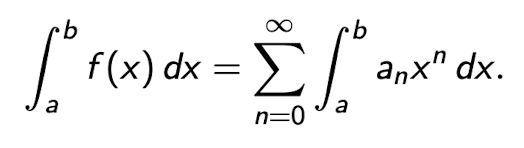IX Integralrechnung und Differentiation

Definition - Stammfunktion

∀∈⊂→⟹∃δε∞ξ⇔∩αβγ∘≈

Es sei I ⊂ R ein Intervall und f(x) : I → R eine Funktion. Eine differenzierbare Funktion F : I → R mit der Eigenschaft:

F’ (x) = f(x), x ∈ I

nennt man Stammfunktion von f auf dem Intervall I.

Satz - Hauptsatz der Integral- und Differentialrechnung:

Es sei f : [a, b] → R stetig. Dann ist für alle C ∈ R die folgende Funktion F : [a, b] → R eine Stammfunktion von f:

F(x) := ∫_a^x f(y) dy + C

Ausserdem ist jede Stammfunktion von der obigen Form.

Korollar - Stetig differenzierbar:

Es sei F : [a, b] → R stetig differenzierbar. Dann gilt für alle x ∈ [a, b]:

F(x) = F(a) + ∫_a^x F’(t) dt

Korollar - Differenz des Integrals:

Es sei f : [a, b] → R stetig und F : [a, b] → R eine Stammfunktion von f. Dann gilt:

∫_a^b f(t) dt = F(x)|_a^b = F(b) - F(a)

Satz - Partielle Integration (Produktregel):

Es seien f, g : [a, b] → R zwei stetig differenzierbare Funktionen. Dann gilt:

∫_a^b f(x) g’(x) dx = f(x) g(x) |_a^b - ∫_a^b f’(x) g(x) dx

Satz - Substitution, Version 1 (Kettenregel):

Es seien I, J ⊂ R zwei Intervalle, f : I → J stetig differenzierbar und g : J → R stetig. Dann gilt für alle [a, b] ⊂ I:

∫_a^b g(f(x)) f’(x) dx = ∫_f(a)^f(b) g(y) dy

Erinnerung: (g ∘ f)’ = g’(f) * f’

Satz - Substitution, Version 2:

Es seien I, J ⊂ R zwei Intervalle, f : I → J stetig differenzierbar und g : J → R stetig. Für [a, b] ⊂ I gelte f’(x) ≠0 für alle x ∈ [a, b] und es sei f ^-1 : [f(a), f(b)] → R die Inverse von f |_{[a, b]}.

Dann gilt:

∫_a^b g(f(x)) dx = ∫_f(a)^f(b) g(y) (f ^-1)’(y) dy

Definition - Lineare Approximation / Tangentenapproximation / 1. Taylor Approximation:

Da Polynome relativ einfach zu behandelnde Funktionen sind, liegt es nahe, kompliziertere Funktionen mit Polynomen zu nähern. Dabei müssen wir aber einen Referenzpunkt x₀ wählen. Die einfachste Möglichkeit bietet:

f(x) ≈ f(x₀) + f’(x₀)(x - x₀) = P₁(x)

P_n(x) wird n-tes Taylorpolynom oder Taylorpolynom vom Grad n genannt.

Satz - Taylor-Approximation mit Integral-Restterm:

Es sei n ≥ 1, f : [a, b] → R eine n-fach stetig differenzierbare Funktion und x₀ ∈ [a, b]. Dann gilt für alle x ∈ [a, b]:

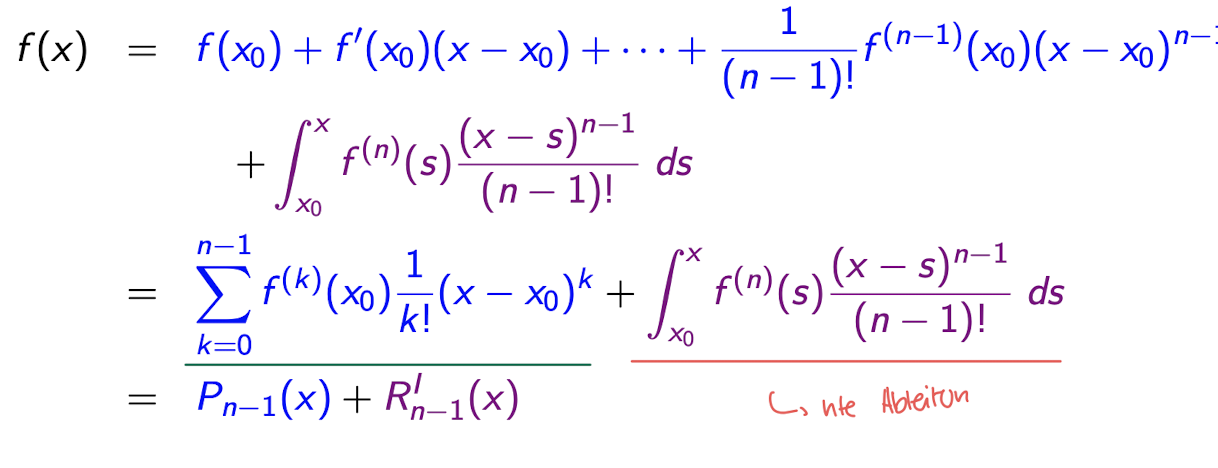
Satz - Taylor-Approximation mit Lagrange-Restterm:

Es sei n ≥ 1, f : [a, b] → R eine n-fach stetig differenzierbare Funktion und x₀ ∈ [a, b].

Dann gibt es für alle x ∈ [a, b] ein ξ ∈ (x₀, x), sodass:

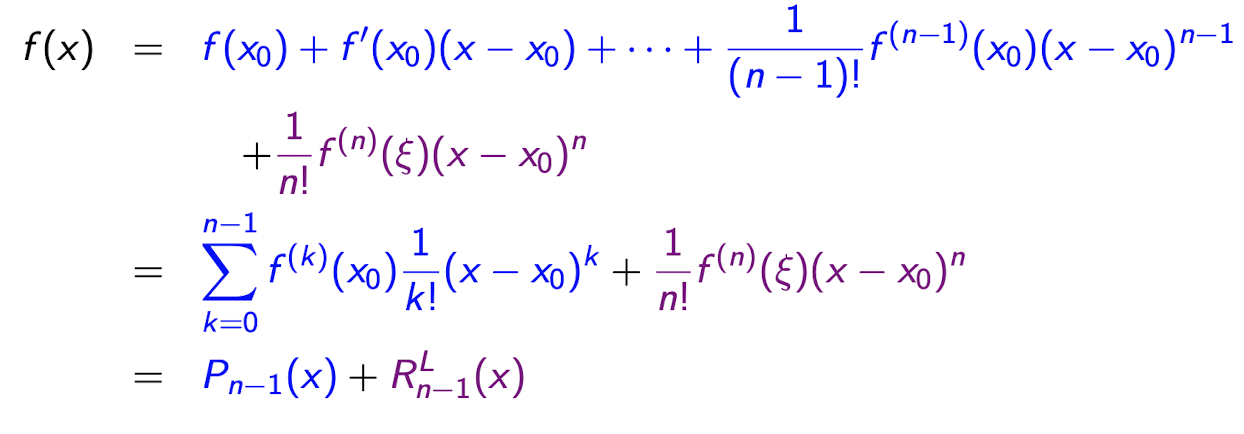
Satz - Taylor-Approximation mit O-Restterm:

Es sei n ≥ 1, f : [a, b] → R eine n-fach stetig differenzierbare Funktion und x₀ ∈ [a, b].

Dann gilt für alle x ∈ [a, b] und x |→ x₀ :

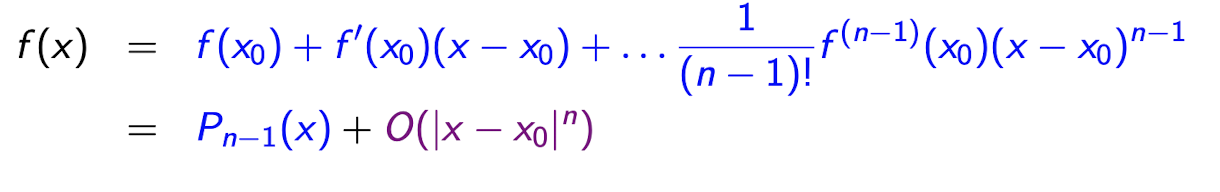
Satz - Taylor-Approximation mit o-Restterm:

Es sei n ≥ 1, f : [a, b] → R eine n-fach stetig differenzierbare Funktion und x₀ ∈ [a, b].

Dann gilt für alle x ∈ [a, b] und x |→ x₀ :

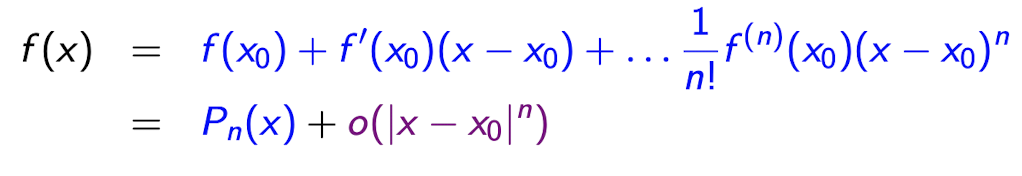
Definition - Taylorreihe / Taylorentwiklung

Für eine gegebene Funktion f heisst die Reihe:

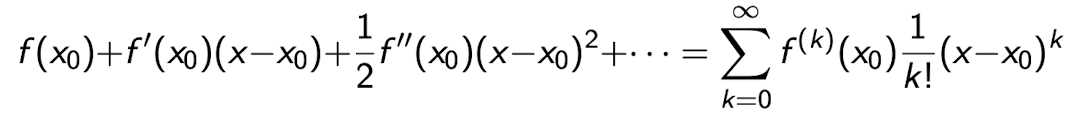
Definition - analytisch:

Es sei I ⊂ R ein Intervall und es sei x₀ ∈ I. Eine glatte Funktion f : I → R heisst an der Stelle x₀ analytisch, falls ein δ > 0 existiert, sodass die Taylorreihe von f um den Punkt x₀ Konvergenzradius R > δ hat und es gilt:

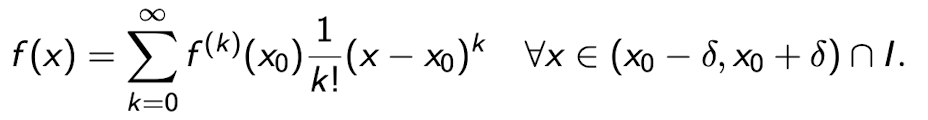
f nennen wir auf ganz I analytisch, falls f in jedem Punkt von I analytisch ist.

Satz - Analytisch:

Es sei I ⊂ R ein Intervall und f : I → R eine glatte Funktion. Ausserdem sei x₀ ∈ I und es existieren Konstanten r, c, A ∈ R mit:

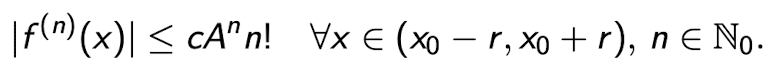
Dann ist f an der Stelle x₀ analytisch.

Korollar - Analytische Funktion:

Es sei f : [a, b] → R eine glatte Funktion. Ausserdem existieren Konstanten c, A ∈ R mit:

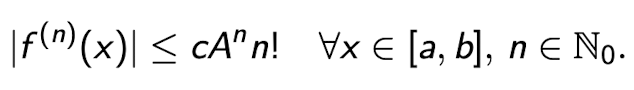
Dann ist f auf [a, b] analytisch.

Satz - Potenzreihen:

Satz - Termweises Ableiten:

Wir beginnen mit der Darstellung einer Funktion durch eine Potenzreihe:

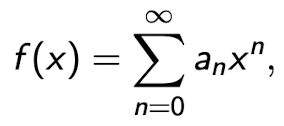
dabei ist wiederum x im Konvergenzintervall I.

Dann ist f differenzierbar, und es gilt:

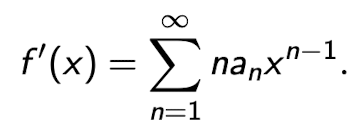
Satz - Termweises Integrieren:

Wir beginnen mit der Darstellung einer Funktion durch eine Potenzreihe:

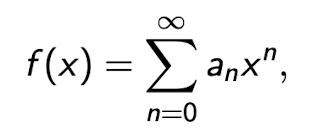
dabei ist wiederum x im Konvergenzintervall I.

Dann ist f auf dem Intervall [a,b] ⊂ I integrierbar, und es gilt: