PURE

formula for area of the sector of a circle in radians

A= 1/2 x r^2 x θ

formula for length of an arc in radians

r x θ = l

Small Angle Approximation: sinθ, tanθ , cosθ

sin θ = θ

tan θ = θ

cos θ = 1 - (θ^2)/2

in binomial expansions, what steps do you take when it says "using your expansion of (*function) estimate the value of (number*^(power of function))" to solve?

-you equate the number to the function then solve for x

-sub in the x value into your expansion

What is a unit vector?

A vector with the magnitude of 1, a unit vector in the direction of a is a/[a]

what is a position vector?

The position of a point relative to the origin

1 + tan^2x

= sec^2(x)

1 + cot^2x

cosec^2x

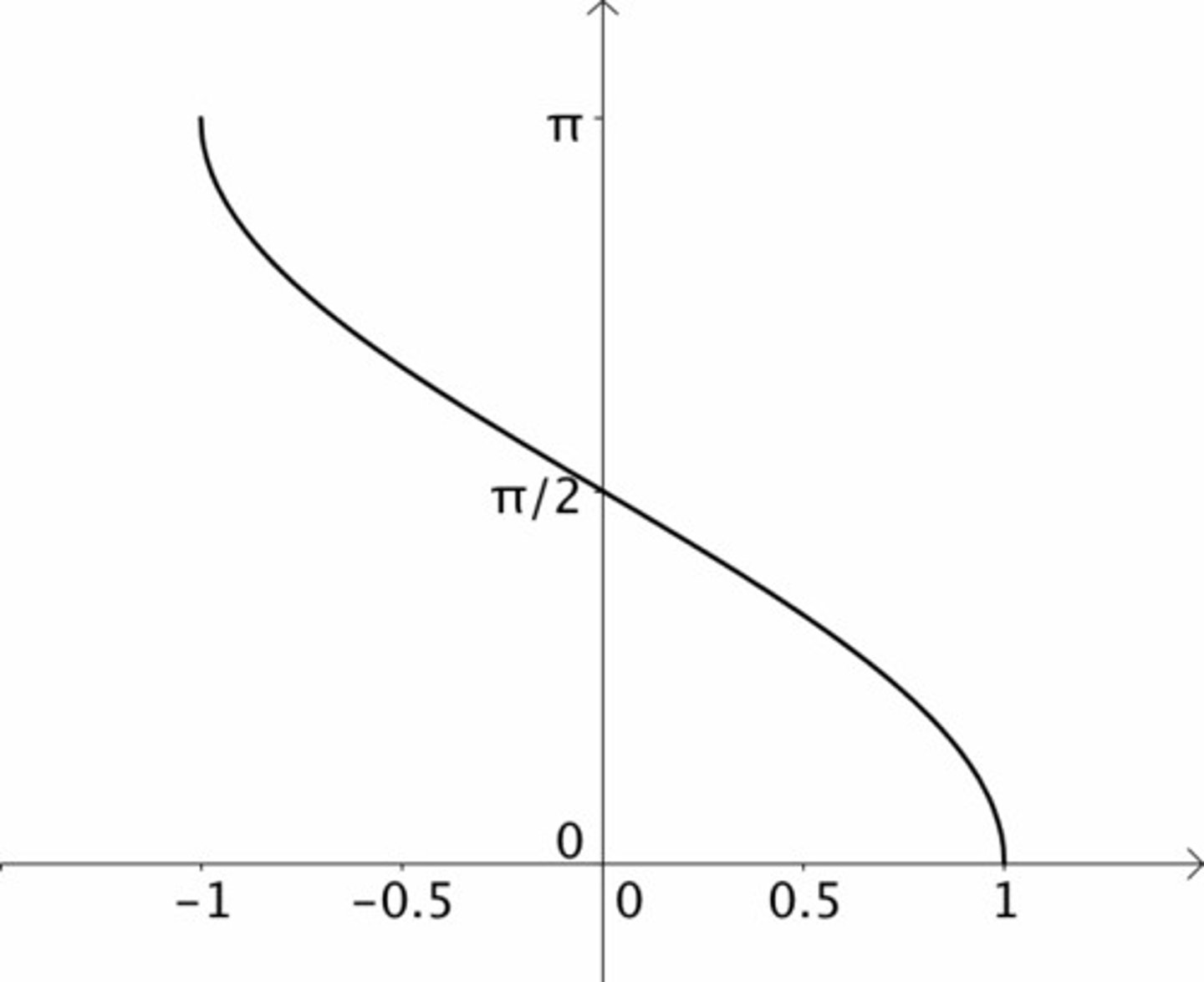
arcos graph domain and range

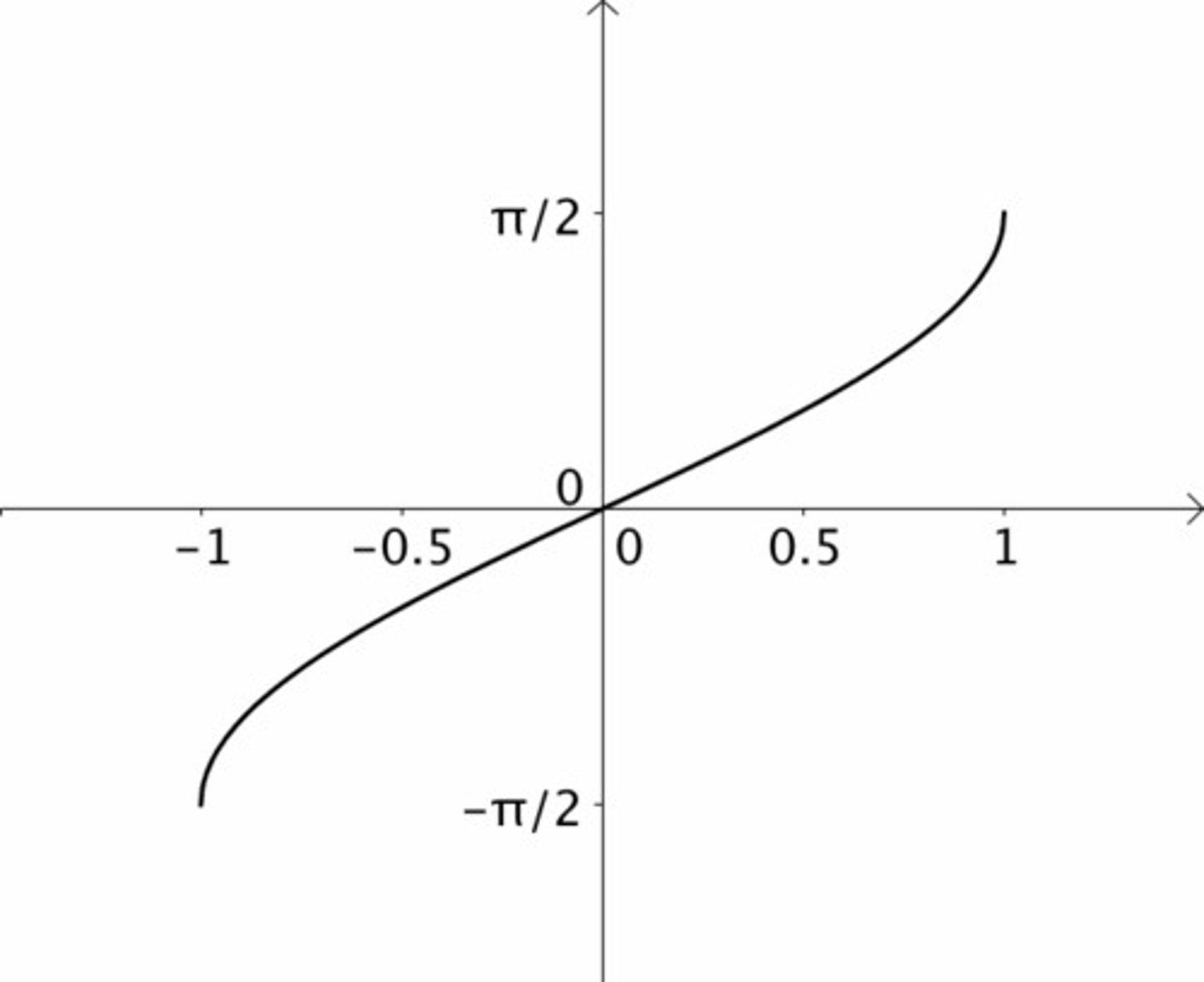
Arcsin graph domain and range

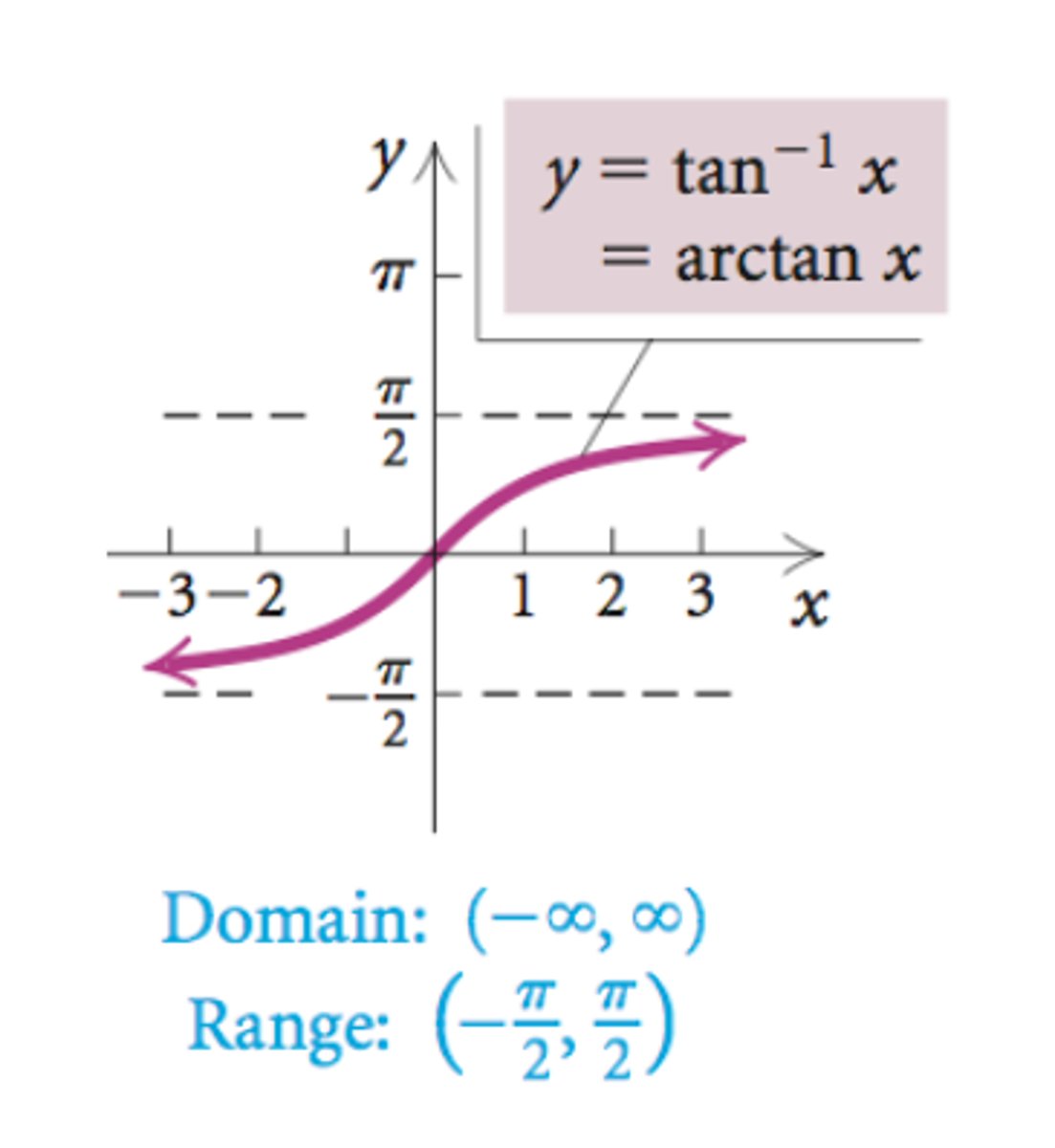
Arctan graph, domain, and range

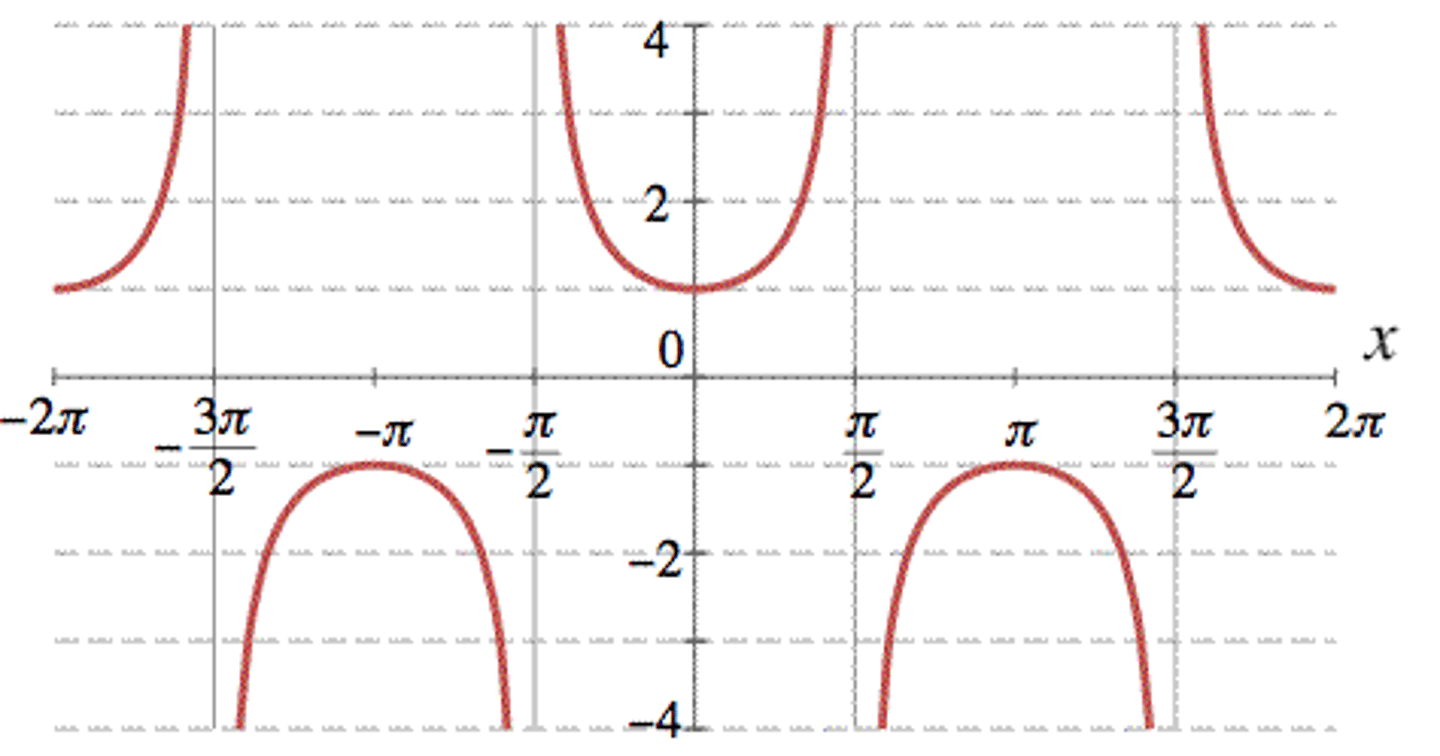
sec x graph

cosec x graph

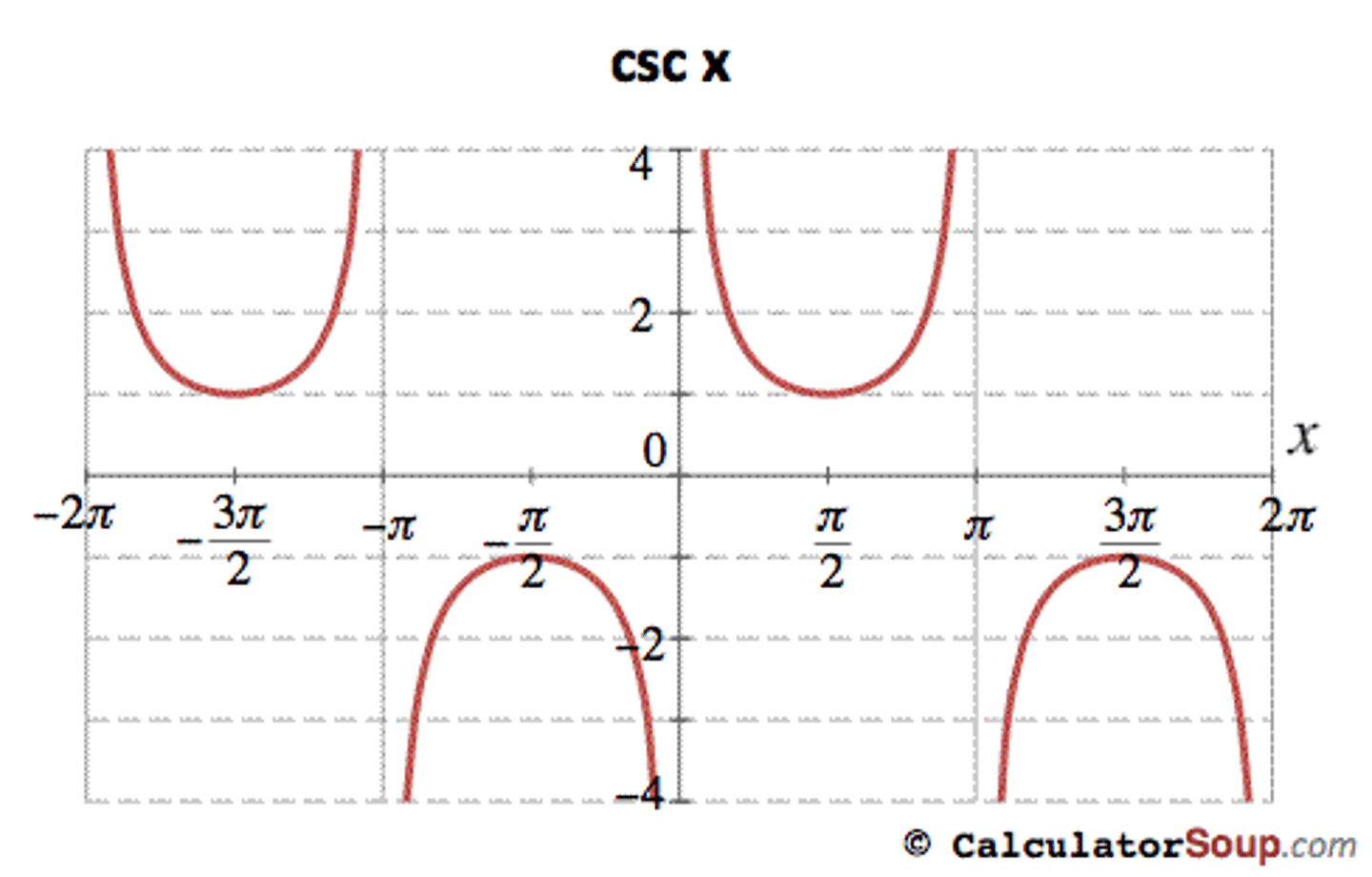
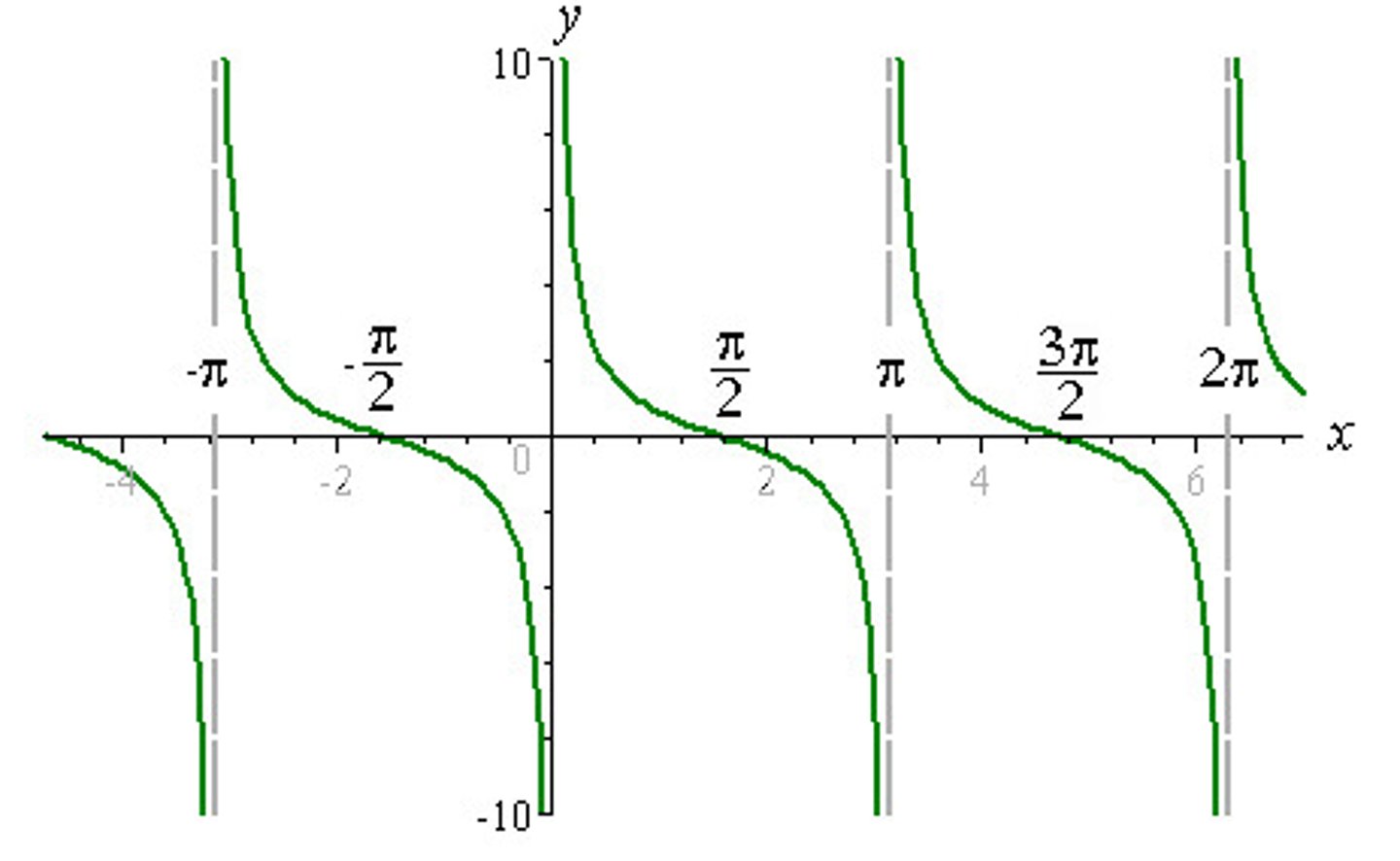
cot x graph

Sin 2A = ?

Sin 2A = 2 SinA CosA

Cos 2A = ?

cos (2A) = cos²(A) - sin²(A)

= 2Cos²A - 1

= 1 - 2Sin²A

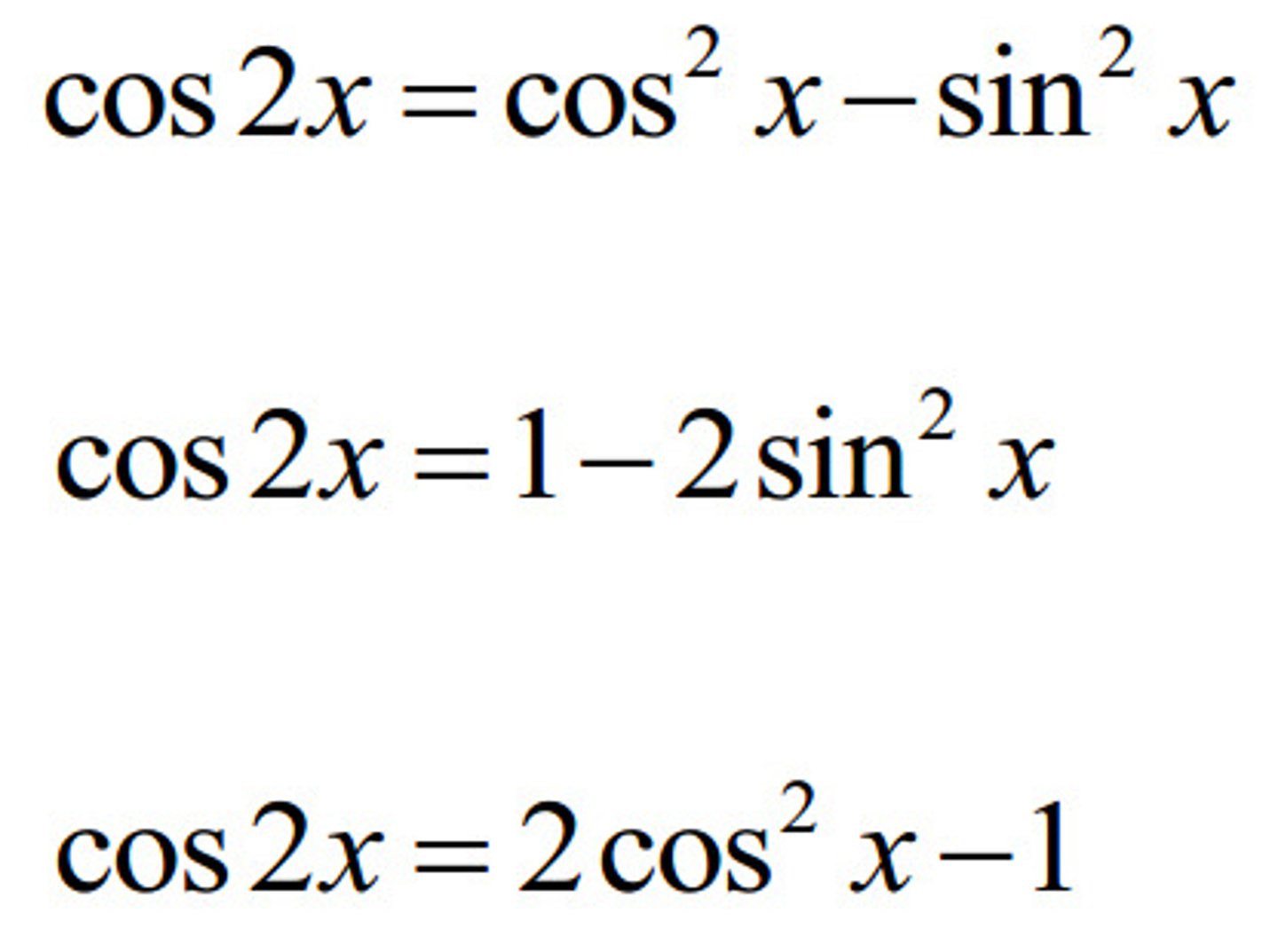
Tan 2A = ?

(2 tan A) / (1 - tan² A)

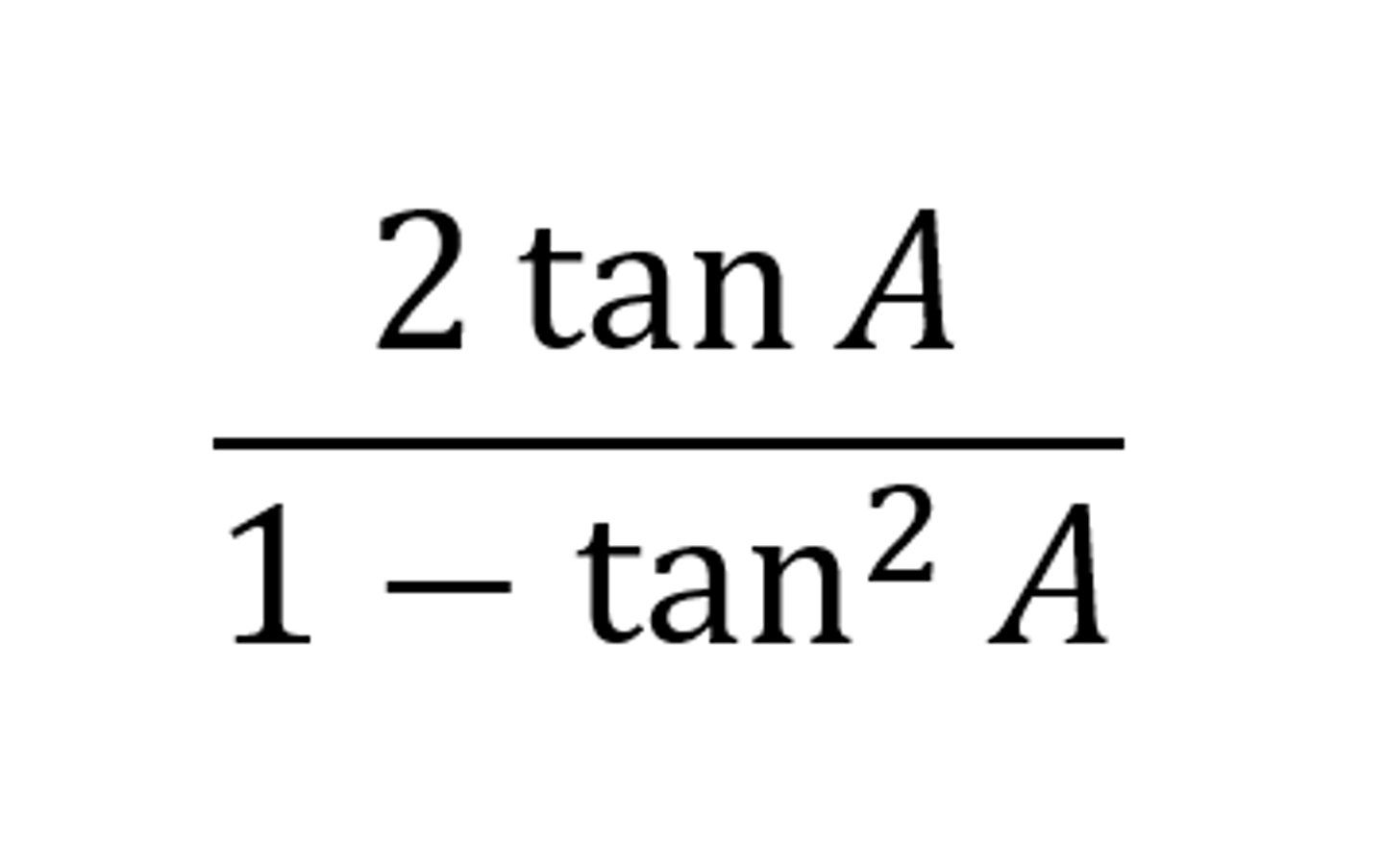
d/dx cotx

-cosec²x

d/dx tanx

sec²x

d/dx secx

secxtanx

d/dx cosecx

-cosecxcotx

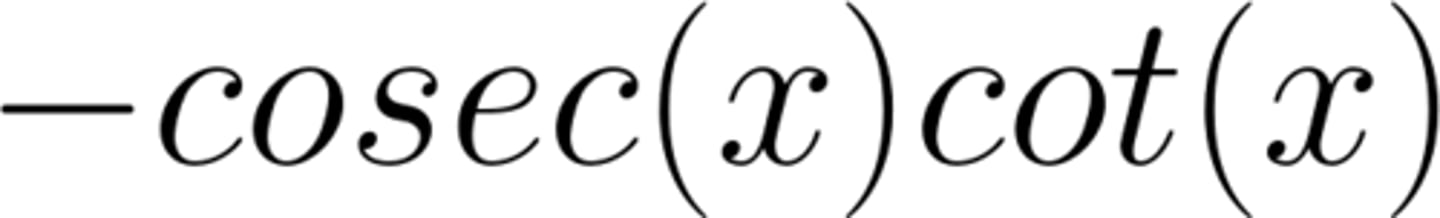
sin(A+B)=

sin(a)cos(b)+cos(a)sin(b)

cos(A+B)=

cos(a)cos(b)-sin(a)sin(b)

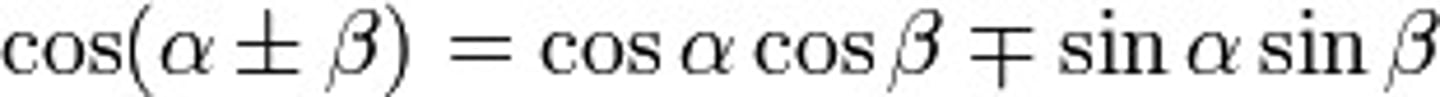
tan(A+B)=

(tanA + tanB)/(1 - tanAtanB)

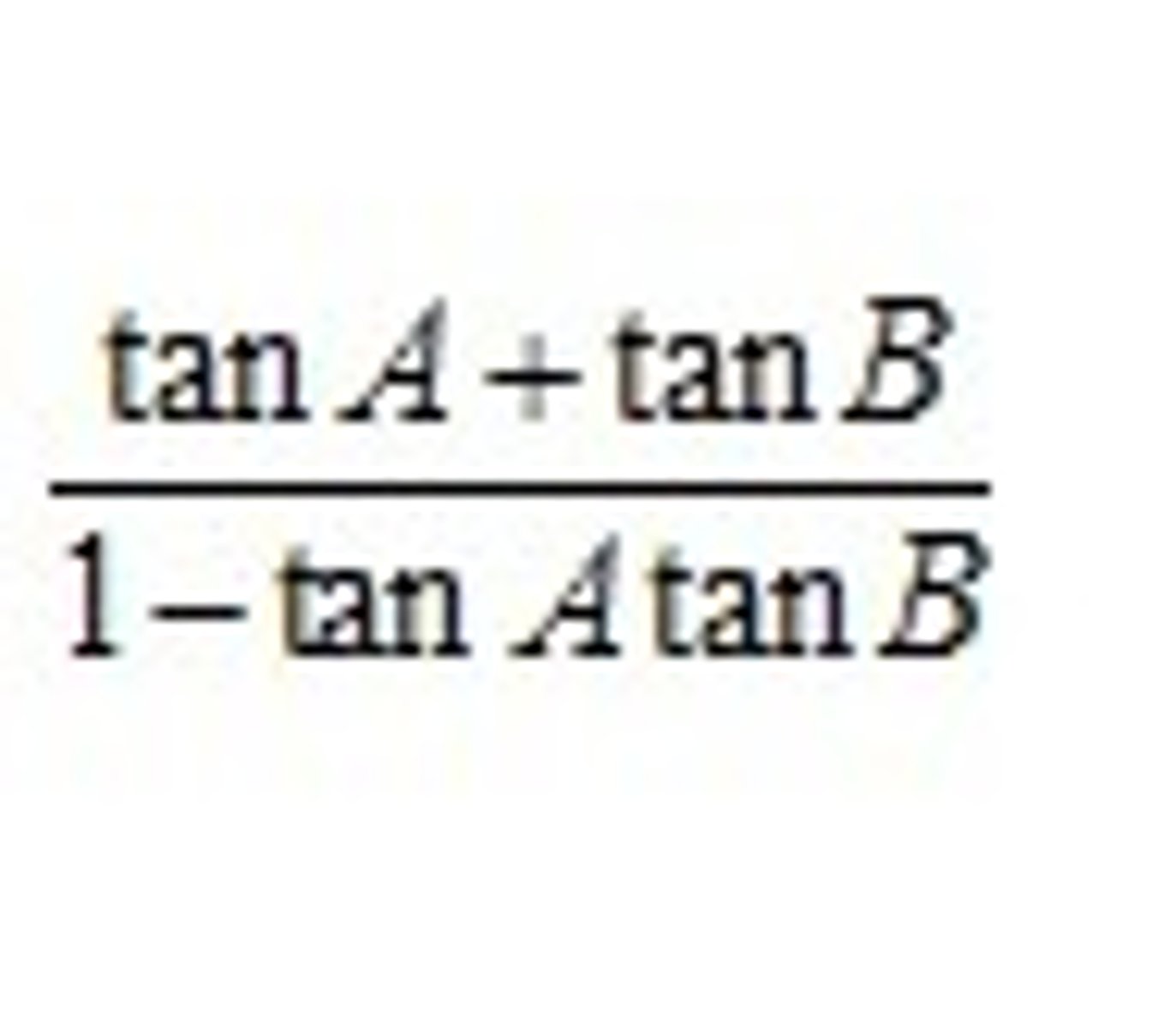
d/dx 2^x

what is the general rule to solving d/dx a^bx

ln2 * 2^x

- ln(base) x (original function) x (derivative of original function)

define sequence

define series

sequence - list of terms

series - the sum of a list of terms

nth term of an arithmetic series

a + (n-1)d

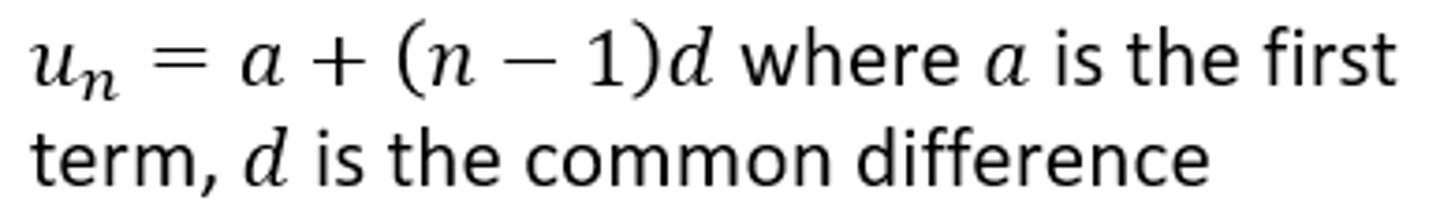
sum of n terms of an arithmetic series

n/2(2a+(n-1)d)

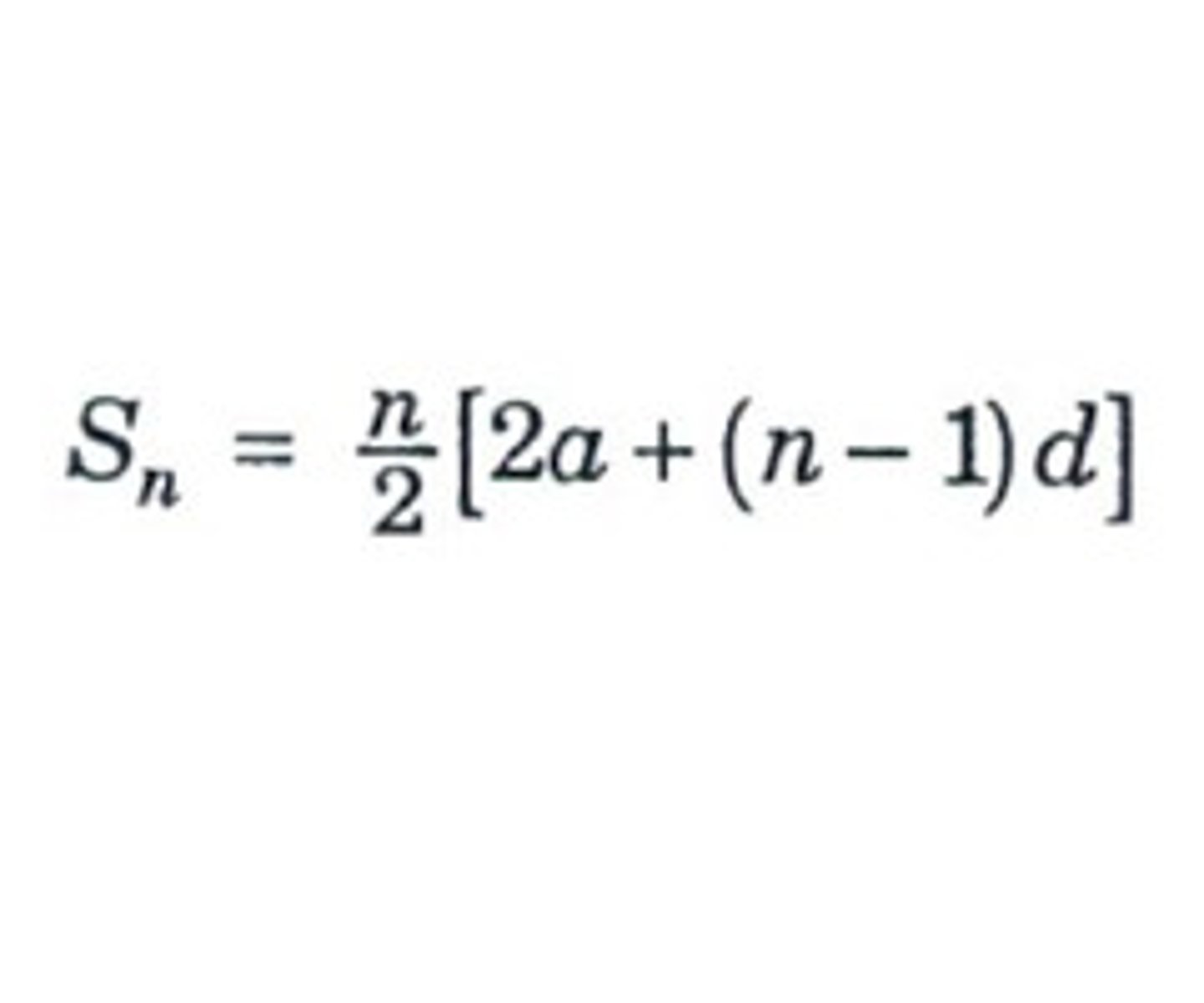
what is a geometric sequence?

geometric sequence - multiplying by a common ratio, r, to get from one term to the next

nth term of a geometric sequence

an=a1(r)^n-1

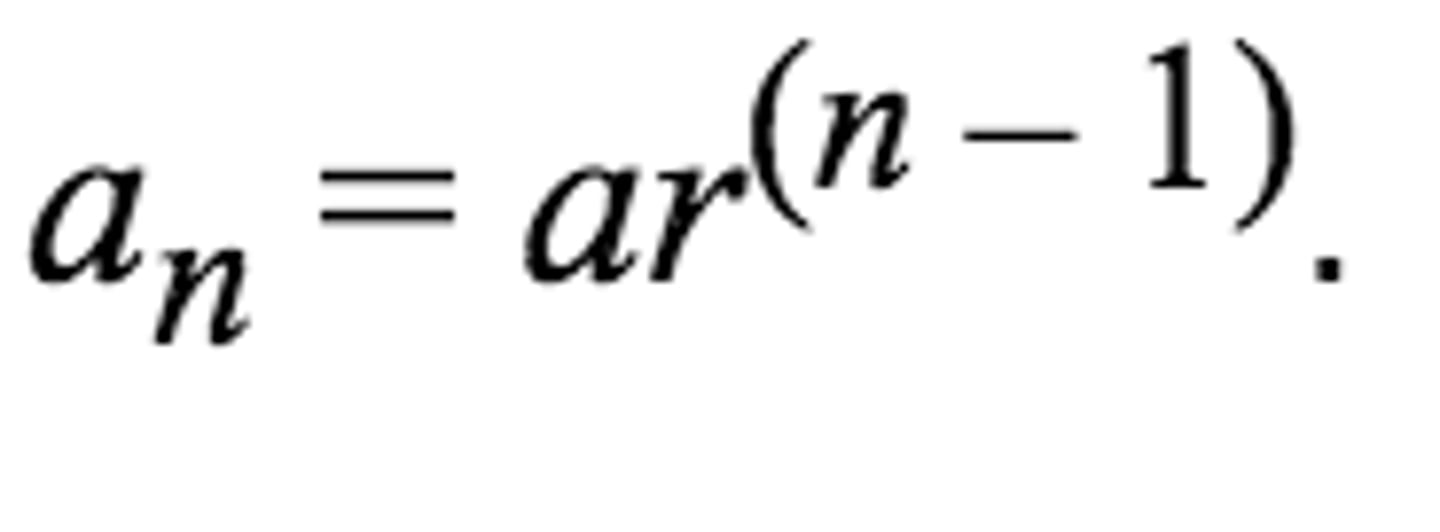
Sum of the first n terms of a geometric series

Sn = a(1-r^n)/1-r

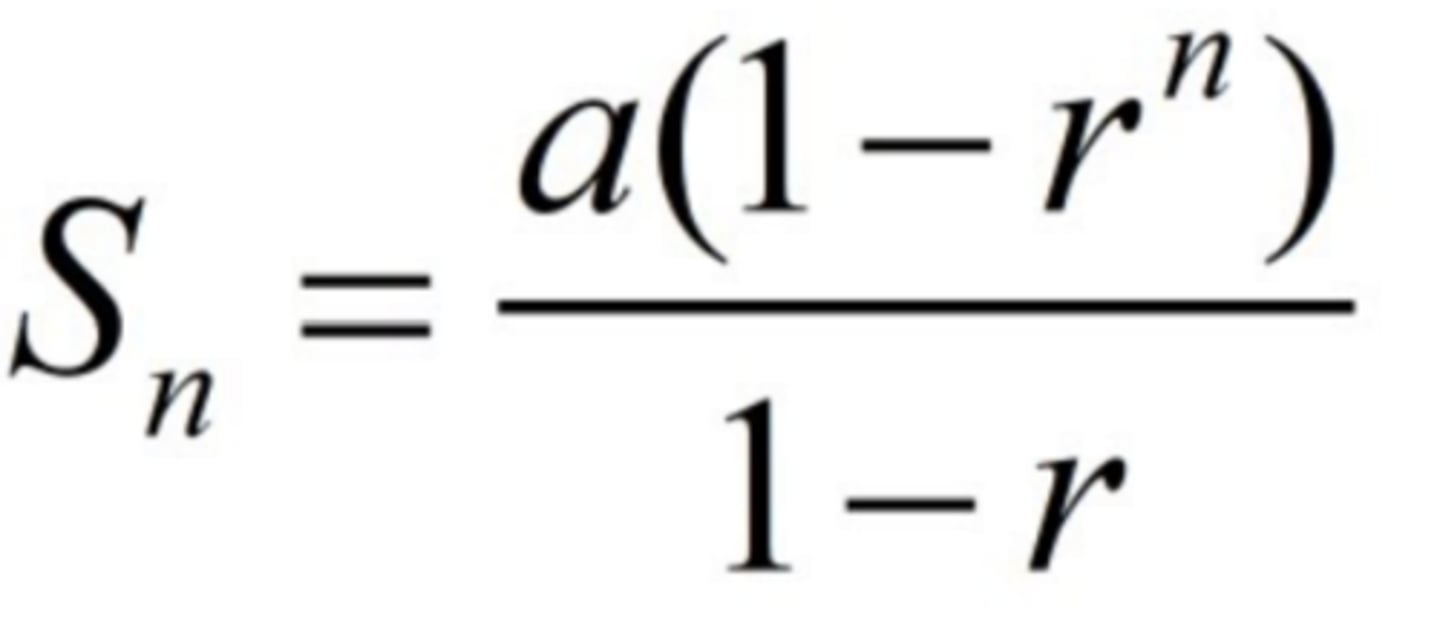
define divergent

define convergent

divergent - when each term is bigger than the previous

convergent - when the terms tend to 0

sum to infinity of a geometric sequence

S= a/1-r

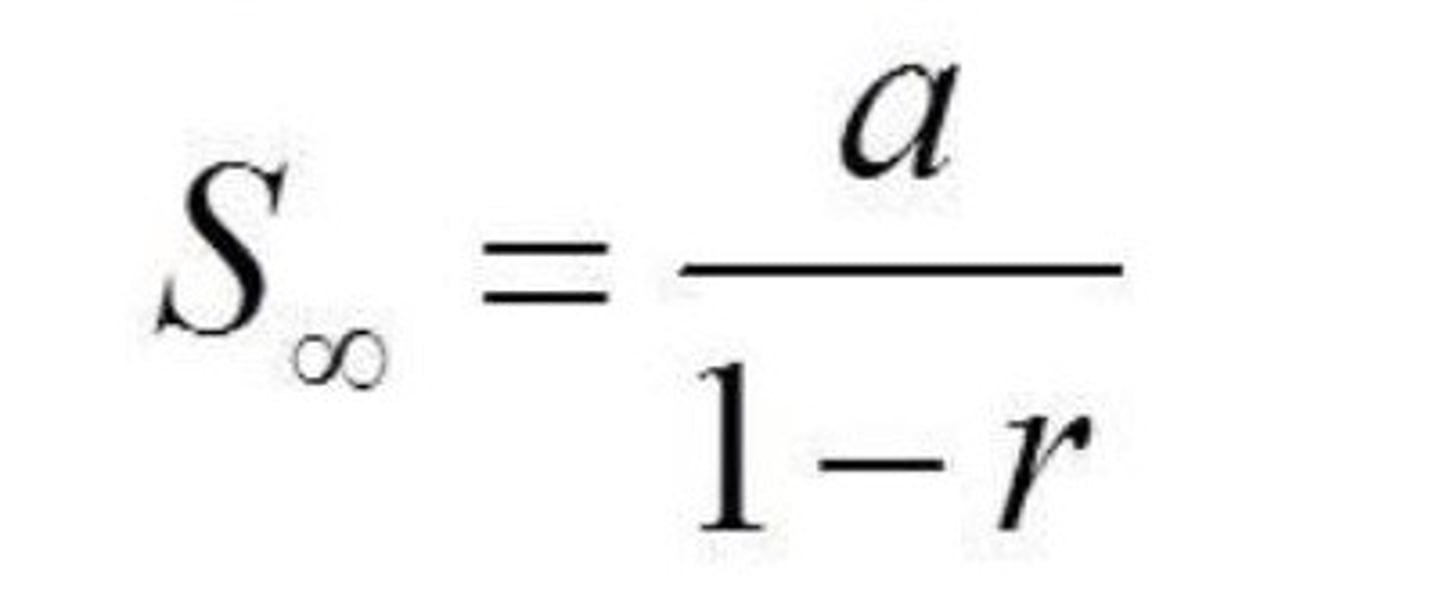
Proof for sum in arithmetic sequence

1) Sn = a + (a+d) + (a+2d) ...

2) Sn = (a+(n-1)d) + (a+(n-2)d) + (a+(n-3)d) ...

1) + 2) = 2Sn = n(2a+(n-1)d)

Sn = 0.5n(2a+(n-1)d)

Proof for sum in geometric series

Sn = a + ar + ar^2

rSn = ar + ar^2 + ar^3

Sn - rSn = a - ar^n

Sn(1-r) = a - ar^n

Sn= (a-ar^n)/(1-r)