Week 6 - Unsupervised learning

Within-cluster variance

The Euclidean distance to define for a cluster C_k of points p ∈ R^D

How to calculate the within-cluster variance?

(1/size of the cluster)*the sum of the square of distances between every distinct pair of points in our cluster

Why do we use the within-cluster variance?

To create a cluster assignment with as low variance as possible

K-means clustering algorithm steps

1. Select K different data points to be the initial cluster centre at time t = 0
2. At time t, assign each data point to the cluster C_k^(t) with the closest cluster centre μ_k^(t - 1)
3. For each cluster, recalculate their cluster centres as the average of all points in the cluster
4. If the clusters have changed go to step 2 movie time to t + 1. Else, stop and return final clusters

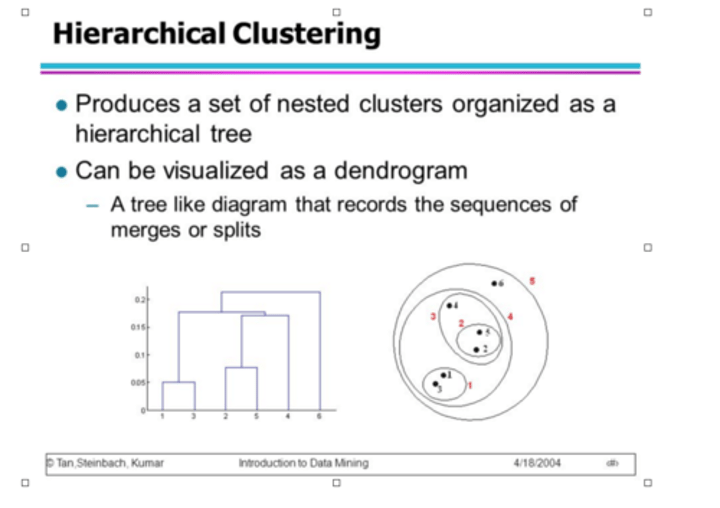
Hierarchical clustering

A set of nested clusters organized as a hierarchical tree

Linkage criterion

Defining the distance between two clusters

Metric

Defining the distance between two points

Manhattan distance metric

The sum of all real distances between two points

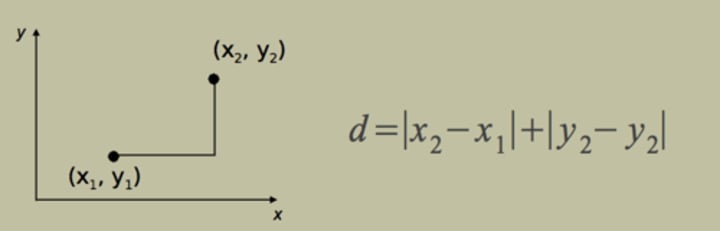
Euclidean distance metric

The shortest path between two points

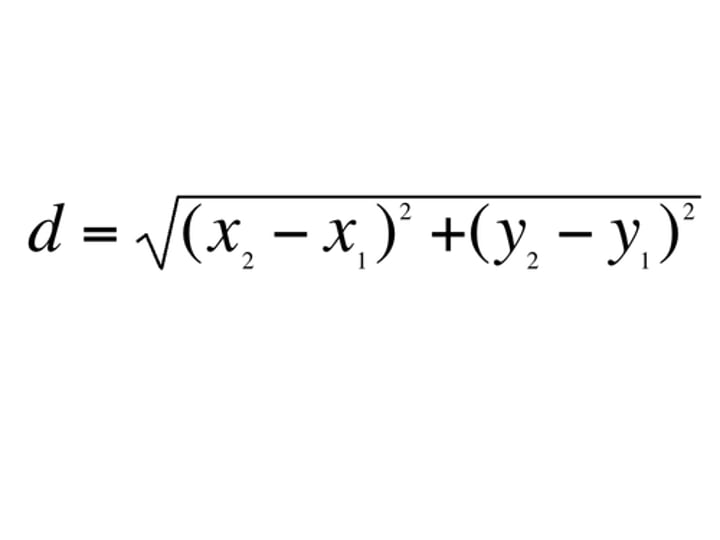
Single-linkage criterion

The minimum (best case) of distances between points from one cluster to another

Complete-linkage criterion

The maximum (worst case) of distances between points from one cluster to another

Average-linkage criterion

The average distance between points from one cluster to another

Dendograms

Diagrams that quickly visualise the entire hierarchical clustering process