Chapter 1 - 2

• In a matrix, it is common convention to represent each example as a separate row or column?

• the iris data set consists of 150 examples and four features which can be written as a ____ x ____ matrix

• the superscript ith superscript will refer to what?

• the subscript jth will refer to what?

• In a matrix, it is common convention to represent each example as a separate row

• the iris data set consists of 150 examples and four features which can be written as a 150 × 4 matrix

• the ith superscript will refer to the ith training example

• the subscript jth will refer to the jth dimension of the training dataset

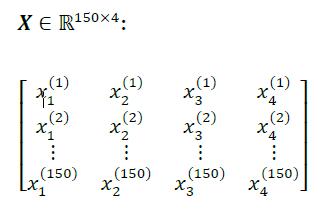
• lowercase bold face letters refer to what?

• uppercase bold face letters refer to what?

• lowercase bold face letters refer to vectors

• uppercase bold face letters refer to matrices

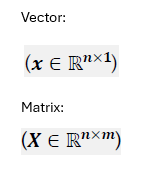
X⁽ⁱ⁾

• here X upper case so it’s referring to a ________

• what is the superscript referring to about this matrix

• X⁽ⁱ⁾ is referring to a matrix and the superscript is referring to the ith row of the matrix

in the example the matrix has 150 rows and 4 columns

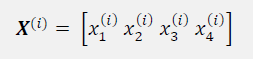
x_j

• here x is lowercase

The learning rate, n (eta) as well as the number of epochs (n_iter), are the so-called what?

Hyperparameters (or tuning parameters)

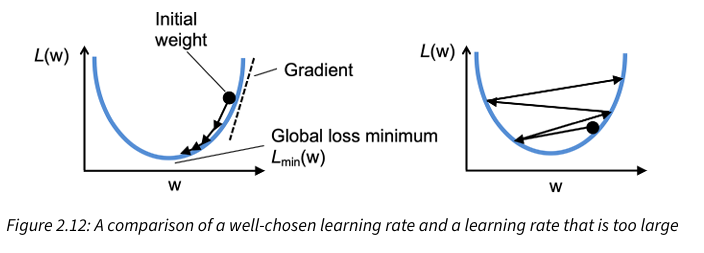
What might happen is we choose a learning rate that is too large? What happens if the learning rate is too small?

We overshoot the global minimum, see figure. The left figure shows a well-chosen learning rate, while the figure on the right shows what happens when we choose a learning rate that is too large

If the learning rate is too small then the algorithm would require a very large number of epochs to converge to the global minimum

Why is the feature scaling method standardization and feature scaling in general used? How do you apply it?

Feature scaling is used to optimize machine learning algorithms, gradient descent is one of the many algorithms that benefits from feature scaling

Standardization is a normalization procedure that helps gradient descent learning to converge more quickly but it does not make the original dataset normally distributed (when most of the values are centered around the mean). It only rescales and recenters the data - it does not change the shape of the distribution. Standardization shifts the mean of each feature so that it is centered at zero and each feature has a standard deviation of 1 (unit variance)

To standardize the jth feature, subtract the sample mean, from every training example and divide it by the standard deviation.

In the attached image, xj is a vector consisting of the jth feature values of all training examples, n, and this standardization technique is applied to each feature, j, in our dataset

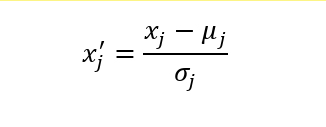
Why does standardization hep with gradient descent learning?

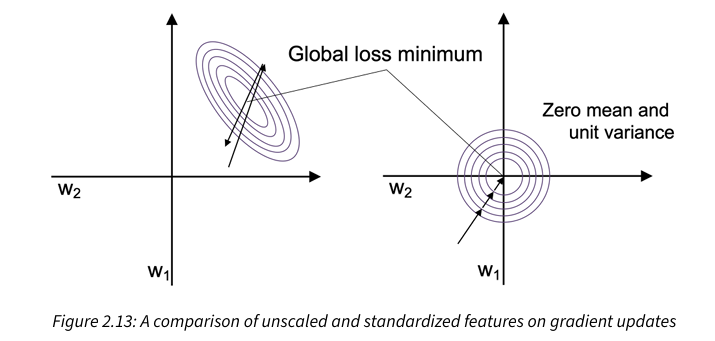
It makes it easier to find a learning rate that works well for all the weights and the bias. When the features are on vastly different scales, a learning rate that works well for updating one weight might be too large or too small to update the other weight equally well. Standardization features can stabilize the training such that the optimizer has to go through fewer steps to find a good or optimal solution (the global loss minimum)

The attached image shows gradient descent with unscaled features (left) and standardized features (right). The concentric circles represent the loss surface as a function of two model weights in a two-dimensional classification problem.

Why is batch gradient descent computationally quite costly in some scenarios and what is a popular alternative?

Batch gradient descent can be computationally costly because it requires the loss gradient to be calculated from the whole training dataset every time we update the weights since we need to reevaluate the whole training dataset each time we take one step toward the global minimum.

A popular alternative to the batch gradient descent algorithm is stochastic gradient descent (SGD). Instead of updating the weights based on the sum of the accumulated errors over all the training examples, with SGD we update the parameters incrementally for each training example.

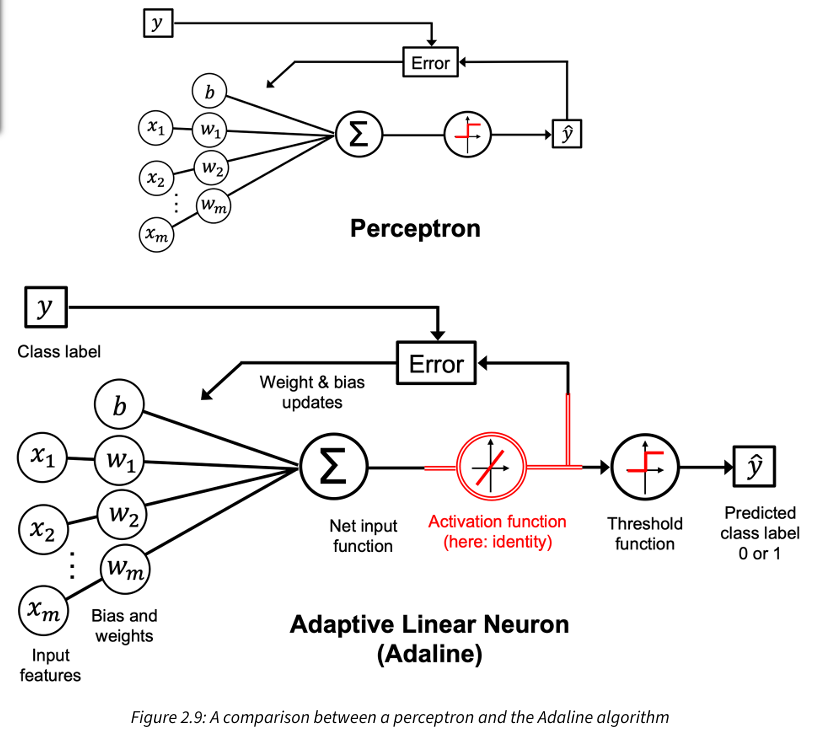
What is the difference between the perceptron and Adaline learning algorithm?

The Adaline algorithm updates the weights based on a linear activation function rather than a unit step function like in the perceptron. In Adaline, the linear activation function, is simply the identify function of the net input. We still use a threshold function to make the final prediction. In other words, in Adaline, we compare the true class labels with the linear activation function’s continuous valued output to compute the model error and update the weights. In contrast the perceptron compares the true class labels to the predicted class labels.

Adaline uses batch gradient descent, meaning weight update is calculated based on all examples in the training dataset (instead of updating the parameters incrementally after each example)

What is the objective function to be optimized during learning process in the case of Adaline?

The objective function to be optimized in the case of Adaline is the loss function, L, used to learn the model parameters knows as the mean squared error (MSE) function, which calculates the mean squared error between the calculated outcome and the true class label.

A few things to note about the MSE

• it’s a continuous linear activation function in contrast to the unit step function

• it’s differentiable

• it’s convex, allowing us to use gradient descent to find the weights that minimize the loss function by finding the global minimum

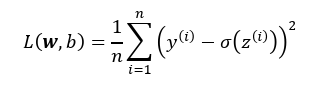
What is the main idea behind gradient descent?

Gradient descent is like climbing down a hill until a local or global loss minimum is reached. In each iteration we take one step in the opposite direction of the gradient, where the step size is determined by the value of the learning rate, as well as the slope of the gradient (the graph only shows this for a single weight for simplicity)

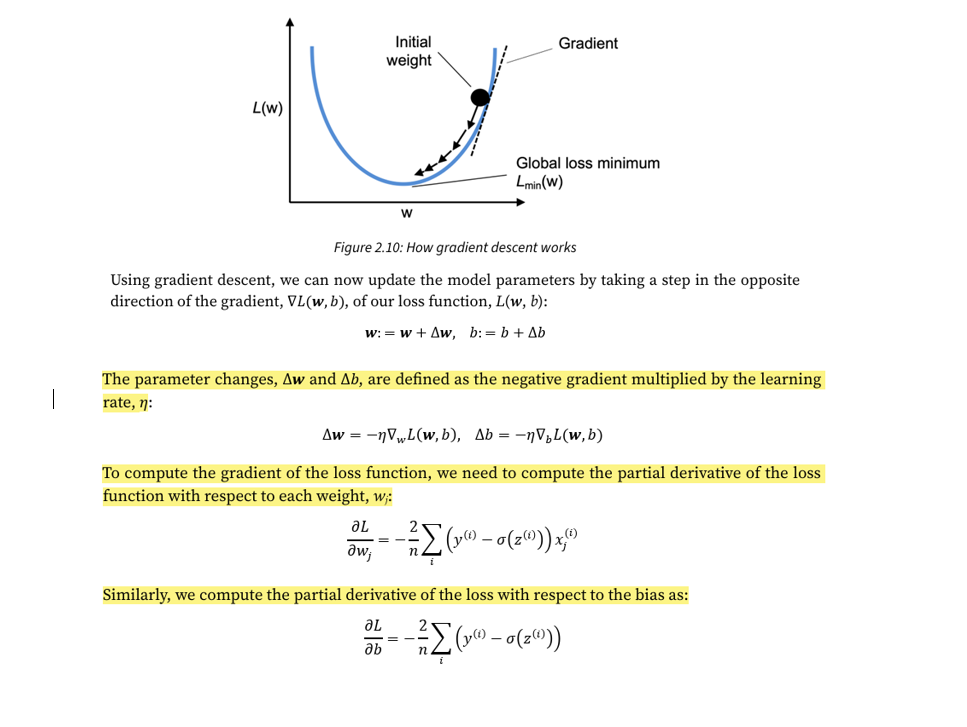
Image of Adaline/batch gradient descent weight update formula vs Stochastic Gradient Descent weight update formula

• SGD typically reaches convergence much faster since it has more frequent weight updates

• the error surface is noisier in SGD due to the gradient being calculated on a single training example, which can help SGD escape shallow local minimum more readily if working with nonlinear loss functions

• when using SGD, present training data in random order by shuffling the training dataset for every epoch

• SGD also has the advantage of bein used for online training meaning that the model can be trained on the fly as new training data arrives