Module 2: Sampling and Introduction to Bivariate Regression

Samples provides estimates of

Population parameters

Whilst samples can be used to make inferences about the population of interest, they can also give…

• Biased estimations

• Different estimates

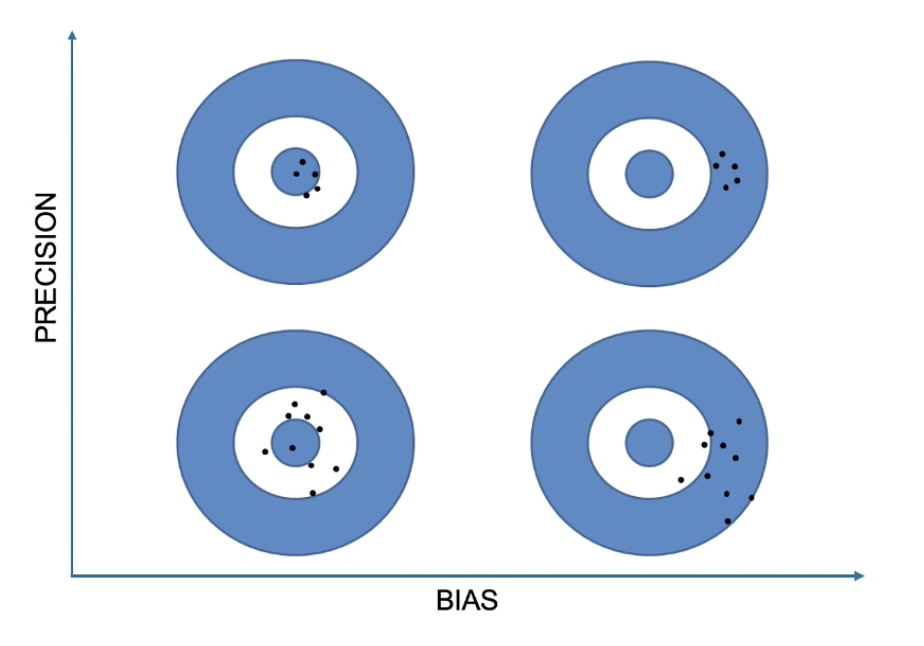
Bias

• Refers to accuracy

• Aggregated means from samples should equal the population mean

• Suggests that the sampling approach tends to zero in on the true underlying parameters

• Important for external validity

Think: In a perfect world, if we measured the mean reading abilities of year 6 classes in a primary school, the school mean should be equal to the population mean of Australian year 6 students.

Bias is a function of _________.

Sampling

• Ensure to get a sample that best represents the population of interest

Precision

• Refers to spread of scores (i.e how much they deviate from the mean)

• Measured by standard deviation

• High precision means that on average, estimates from each sampling occasion are not far from the mean.

High standard deviation score suggests…

Low precision

Low standard deviation score suggests…

High precision

Precision is a function of…

Sample size

• The larger the sample size, the more precise the estimate

Describe the concepts of precision and bias through a target practice analogy. What do the targets look like as precision and bias vary?

Bivariate Regression

• Looks at the relationship between one predictor variable and one outcome variable

  • Think: CorrelationPRO

• When conducted, a correlation statistic is obtained along with additional information inc. but not limited to

  • the slope

  • the intercept

Equation for a straight line

Y = a + bX

a = the intercept

b = the gradient

Formula for Line of Best Fit (Regression Line)

Y’ = predicted value of Y

b₀= INTERCEPT of the regression line (predicted Y value when x = 0)

b₁ = SLOPE of regression line

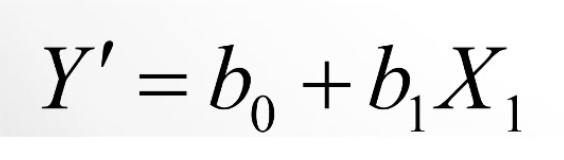
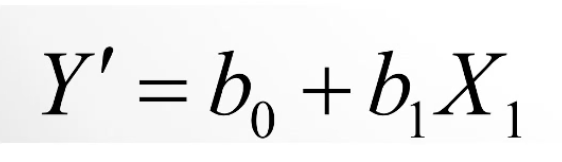
Y’

Predicted value of Y

b₀

INTERCEPT of the regression line (predicted Y value when x = 0)

b₁

SLOPE of regression line

Think: Are you thinking what I’m thinking B1? = slippery slope to anarchy

Formula for the gradient

b = (difference between y scores) / (difference between x scores)

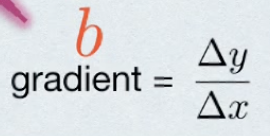
Bivariate Regression: The Slope

The rate at which Y changes with each 1-unit change in X

• Denoted as b₁

Bivariate Regression: The Intercept

Where the line cross the y axis

• represented as a

Why is the straight line equation modified in bivariate regressions?

To include a systematic and random component

• Called ‘line of best fit’

Systematic Component of line of best fit in bivariate regressions

Shows relationship with predictor variable

Random component of line of best fit in bivariate regressions

Unrelated to predictor

Where do you find the b0 and b1 values in SPSS output?

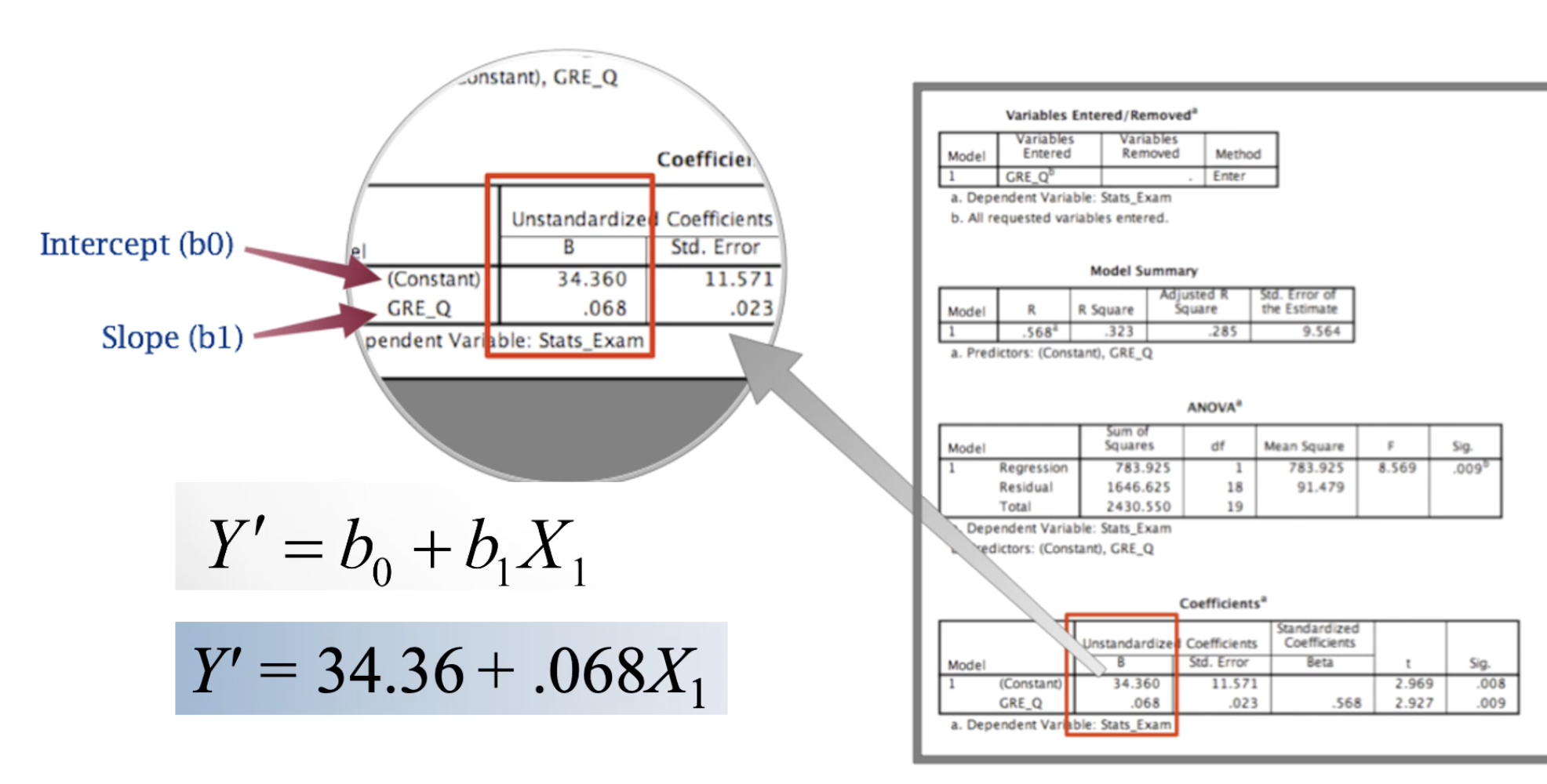
What value in SPSS output from a bivariate regression is the same as the correlation value?

Beta coefficient in the coefficient table

• Located next to the b0 and b1 values

Syntax for Bivariate Regression in SPSS

regression var = variable1 variable2
/dep = responsevar
/enter = predictorvar.

How can you use the slope and intercept values from SPSS to predict scores?

1. Find your slope and intercept

2. Substitute them into the Y’ = b0 + b1X1 equation

3. Put your x value (predictor value) into X1

4. Y’ will be your predicted score, which is a plotted point on the line of best fit

The basic purpose of regression is…

Prediction

Think: A regression is basically a correlation, but if that’s the case, why don’t we just use correlation? Regressions give us the correlation score and a bit more, like the intercept and slope. We can plot a line of best fit on a regression, which gives predictive qualities where there are no data points (not infallible though)

When can errors in prediction arise?

When the residual is not ± 1

r ≠ ± 1

Residual

The difference between the actual score and predicted score

• AKA error

• Predicted scores are susceptible to error when the residual is more than ± 1

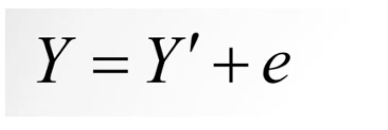
When we are sampling, we are selecting a ______ of a population.

Subset

Using different sampling plans or approaches will ensure….

Accuracy to a certain level in the long run if it is representative.

Define and explain universalistic sampling approaches*

Testing specific theories or hypotheses about the relationships between variables

• Research questions are:

  • How does this work?

  • What is the mechanism?

Think: The ones we usually do where we are trying to find causation

Define and explain particularistic sampling approaches*

• Primary goal is statistical estimation

• Try to capture the range of the underlying parameters

• Descriptive hypotheses

• Research questions include:

  • How many people think like this?

  • How many people have this disorder?

  • How many people would benefit from this treatment?

Think: Trying to find information about the variable, not the relationship between them.

Probability Sampling

Based on random sampling approaches such as:

• Simple Random Sampling

• Stratified sampling

• Cluster sampling

Simple Random Sampling (SRS)

• Every member of the population has an equal and known chance of being selected

• Gold standard but requires very large samples

• Can be expensive and not always feasible

Think: Dury Duty is serious (SRS)

Every adult in the population sample frame) can be selected for dury duty and they know this

Stratified Sampling

The population is divided into subpopulations in some meaningful way to ensure all populations are sampled appropriately

• Strata (subgroups) are created based on particular characteristics

  • Age, gender, profession, etc

• You should sample proportionally to the population

  • I.e. If 70% of psych students are female and that is your population of interest, in a sample of 100, 70 should be female.

Cluster Sampling

Uses subgroups in the population, but samples the entire subgroup rather than basing it on subgroup proportions

Think: If you were interested in Year 9 attitudes towards university, you would sample the subgroup of ‘year 9 students’ from a range of schools.

Advantages of Probability Sampling

• We have a known or estimated probability of inclusion for each sample element which can be factored into final sample

• Lower risk of sampling bias

• Greater external validity

Disdvantages of Probability Sampling

• Expensive

• Often not feasible

Non-probability sampling approaches*

Uses non-random approaches and therefore not every person in the population of interest has an equal and known chance of being included.

Includes:

• Convenience sampling

• Purposive sampling

• Snowball sampling

• Quota sampling

Convenience Sampling

Involves recruiting from a sample of participants that the researcher has access to

• Recruiting whoever we can get

• Most widely used type of sampling in psychology

• Unknown bias can be controlled by increasing precision through sample size

Purposive Sampling

Judgement sampling or known groups sampling

• Researcher makes a judgement based on their expertise to select the best sample

Snowball Sampling

Involves having participants recruit other participants with an increasing number of participants

Think: Pyramid scheme

Quota Sampling

Effectively the same as stratified sampling but using a non-random approach

Think: If 10% of the population in your community were teachers, so you surveyed a bunch of teachers outside of a teacher’s convention. You’d meet your 10% quota but because they travelled to the place, they would not represent the views of teachers in that community.

Advantages of Non-probability samples

• Cheaper

• Easier to access

• Larger samples affords greater precision

Disadvantages of Non-probability samples

• Probability of inclusion is unknown and cannot be calculated

• High risk of unknown bias

• Bias results in abiguity of results

• limits external validity (generalisability)

Define a sampling frame*

A list of people from a population of interest from which we can draw our sample

• List should include the entire population and only those in the population

  • Key to probability sampling

• Serves as a conduit to the population

Think: Phone book, class list, electoral role

Dummy Variables

Categorical variables that have values of 0 and 1

Dummy Variable Conventions

• Largest category is assigned as value ‘1’

• Name the dummy variable after the category assigned variable ‘1’

Cronbach’s Alpha

A measure of internal consistency/reliability.

• a = >0.70 → adequate reliability

• a = >0.80 → good reliability

• a = >0.90 → excellent reliability

0.7 is the benchmark! If it’s less; forget it

3 Strategies for making coding easier in a questionnaire

1. Put answer blocks in left margin

2. Have respondents put their answers on a separate answer sheet

3. Have Ps put their responses on a coding sheet that can be marked electronically

In what sampling method do people have an equal chance of being selected?

Random sampling

When determining the required sample size for random sampling methods, what happens to the sample size as the confidence level increases (error margin decreases)?

The required sample size increases

Rank the following sampling techniques in order of most representative samples to least

• Quota sampling

• Proportionate stratified random sampling

• Random sampling

• Convenience sampling

1. Proportionate stratified random sampling

2. Random sampling

3. Quota sampling

4. Convenience sampling