Graphs

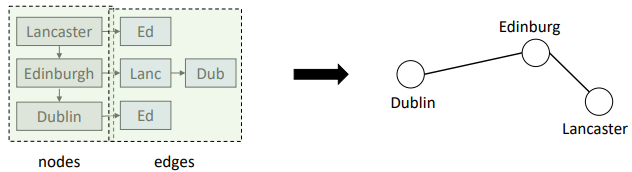
Graph

set of nodes (or vertices) and edges (or arcs/links)

Simple Graph

no self-loops

Labels

values associated to nodes and edges

can be integers, strings etc

natural setting:

• integers for edges (weights)

• names for nodes (identifiers)

Undirected Edges

can be traversed in both directions

Directed Edges

can only be traversed in the indicated direction

Subgraphs

of some graph 𝐺 is a subset of the nodes and edges of 𝐺

For both undirected and directed graph

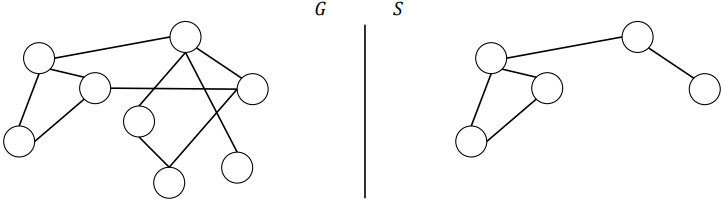
Induced Subgraphs

by subset 𝑈 ⊆ 𝑉 if its nodes are U and its edges are all the edges between nodes in 𝑈 within 𝐺

For both undirected and directed graph

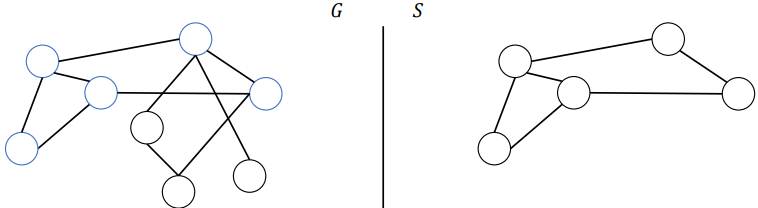
Spanning Subgraphs and Trees

of 𝐺 if it is formed from all nodes of 𝑮 and some of the edges of 𝐺

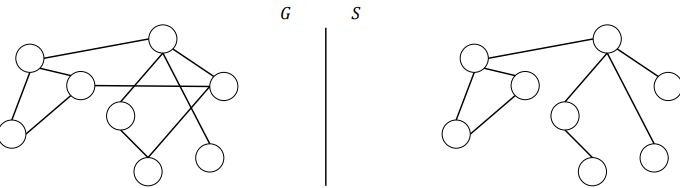
Spanning Tree

spanning subgraph and tree

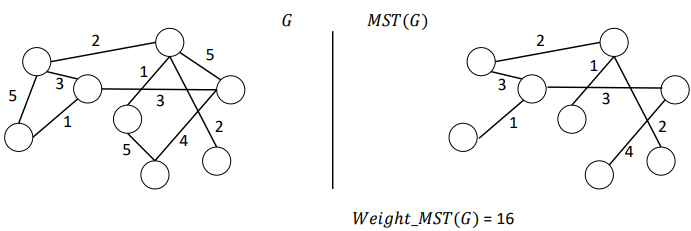
Minimum Spanning Tree

Spanning tree with minimum total sum of edge weights

Complementary Graphs

Same set of nodes and contains all edges that are not in 𝐺

Create a clique (fully-connected graph) and remove the edges that are in 𝐺

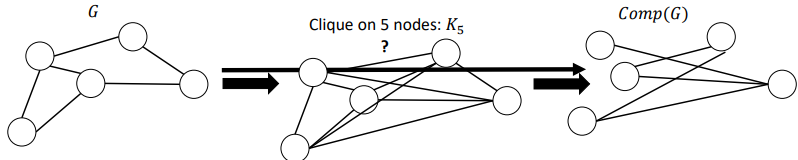
Density

A measure between 0 and 1 that indicates how heavily connected its nodes are

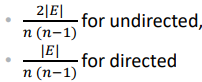
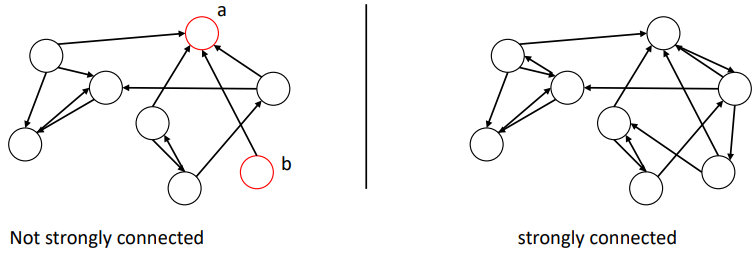
Connectivity

An undirected graph is if there is a path between any two vertices

Directed graph is strongly if we can reach any node from any other

Directed graph is weakly if its undirected version is strongly

Graph ADT

• Common set of operations for graphs,

• But applicable to many different settings (networking, social media, public transport, artificial intelligence,…)

• Basic operations = node and edge additions/removals, and adjacency queries:

void addNode(Node n);
void removeNode(Node n);
void addEdge(Node n, Node m);
void removeEdge(Node n, Node m);
boolean adjacent(Node n, Node m);
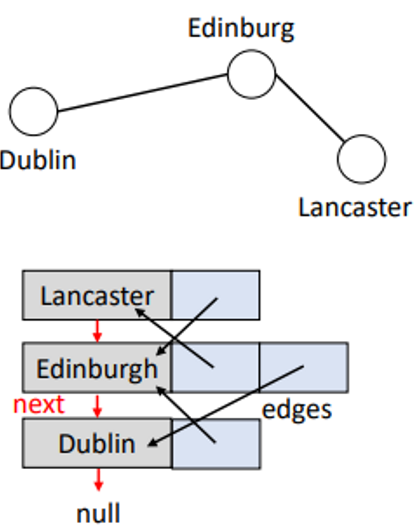
Node[] getNeighbours(Node n);

Graph Encoding via Lists

where the graph is a list of lists

List-Based Implementation

public class GraphList(Lable> {
   GraphNode headNode;

   public class GraphNode<Lable> {
      Label id;
      LinkedHashSet<GraphNode> edges;
      GraphNode next;

      public GraphNode(Label label) {
         this.id = label;
         this.edges = new LinkedHashSet<GraphNode>();
      }
   }

   public GraphList() {
   }
   ...
}

Adding Nodes

public void addNode(Label label) {
   GraphNode node = new GraphNode(label);
   node.next = headNode;
   headNode = node;
}

Finding Nodes

private GraphNode findNode(Label label) {
   GraphNode node = headNode;
   while (node != null) {
      if (node.id == label) return node;
      node = node.next;
   }
   return null;
}

Adding Edges

public void addEdge(Label l1, Label l2) {
   GraphNode node1 = findNode(l1);
   GraphNode node2 = findNode(l2);
   if (node1 != null && node2 != null) {
      node1.edges.add(node2);
      node2.edges.add(node1);
   }
}

Removing Edges

public void removeEdge(Label l1, Label l2) {
   GraphNode node1 = findNode(l1);
   GraphNode node2 = findNode(l2);
   if (node1 != null && node2 != null) {
      node1.edges.remove(node2);
      node2.edges.remove(node1);
   }
}

Removing a Node

public void removeNode(Label label) {
   GraphNode<Label> node = headNode;
   GraphNode<Label> prevNode = null;
   while (Node != null) {
      if (node.id == label) {
         //remove all edges
         for (GraphNode<Label> neighbour: node.edges) {
            removeEdge(node.id, neighbour.id);
         }
         //remove node from the 'list'
         if (prevNode != null) prevNode.next = node.next;
         else headNode = node.next;
      }
      prevNode = node;
      node = node.next;
   }
}

Neighbours

public GraphNode[] getNeighbours(Label label) {
   GraphNode<Label> node = findNode(label);
   GraphNode[] neighbours = node.edges.toArray(new GraphNode[0]);
   return neighbours;
}

Adjacency

public boolean adjacent(Label l1, Label l2) {
   GraphNode n1 = findNode(l1);
   GraphNode n2 = findNode(l2);
   return n1.adges.contains(n2);
}

Displaying the Graph

public void print() {
   GraphNode<Label> node = headNode;
   while (node != null) {
      System.out.print("[ " + node.id + " : ");
      for GraphNode<Label> neighbour: node.edges) {
         System.out.print(neighbour.id + " ");
      }
      System.out.println"]");
      node = node.next;
   }
}

Graph ADT - Memory and Time Complexity

• Memory = 𝑂(𝑁 + 𝐸) for graphs with 𝑁 nodes and 𝐸 edges (memory-efficient)

• Worst-case time complexity:

  • Adding node is 𝑂(1)

  • Removing and finding node is 𝑂(𝑁)

  • Adding and removing an edge is 𝑂(𝑁)

  • Adjacency check is 𝑂(𝑁)

Graph Encoding via Matrices

Use a two-dimensional array called adjacency matrix

• For row 𝑖𝑖 and column 𝑗 (with 𝑖 ≠ 𝑗), 𝐴[𝑖][𝑗] = 1 if and only if there is an edge between nodes 𝑖 and 𝑗

• Adjacency matrix is symmetric for undirected graphs: 𝐴[𝑖][𝑗] = 𝐴[𝑗][𝑖]

Adjacency Matrices

For an undirected graph, two cells are always modified when we add or remove an edge

• The sum value of a row tells us how many edges go out of this node

• The sum value of a column tells us how many edges go in this node

For a directed graph, single sell modified when we add/remove a directed edge

• Read the 1s in row 𝑖 as: “node 𝑖 has an edge to column X”

Adding a Node - Adjacency Matrix

public class GraphMatrix {
   int graph[][];
   int size;

   public GraphMatrix() { this.size = 0;}

   public void addNode() {
      size++;
      int[][] newGraph = new int[size][size];
      for (int i = 0; i < size - 1, i++) {
         for (int j = 0; j < size - 1; j++) {
            newGraph[i][j] = graph[i][j];
         }
      }
      this.graph = newgraph;
   }
...

Removing a Node - Adjacency Matrix

public void removeNode(int k) {
   if (k <= 0 || k > size)
      throw new IllegalArgumentException("Bad Index");
   size--;
   int[][] newGraph = new int[size[size];
   for (int i = 0; i < size; i++) {
      for (int j = 0; j < size; j++) {
         int ip = (I >= k - 1) ? 1 : 0;
         int jp = (j >= k - 1) ? 1 : 0;
         newGraph[i][j] = graph[i + ip][j + jp];
      }
   }
   this.graph = newGraph;
}

Adding Edges - Adjacency Matrix

public void addEdge(int i, int j){
   if (i <= 0 || i > size || j <= 0 || j > size)
      throw new IllegalArgumentException("Bad indices.");
   graph[i-1][j-1] = 1;
   graph[j-1][i-1] = 1;
}

Removing Edges - Adjacency Matrix

public void removeEdge(int i, int j){
   if (i <= 0 || i > size || j <= 0 || j > size)
      throw new IllegalArgumentException("Bad indices.");
   graph[i-1][j-1] = 0;
   graph[j-1][i-1] = 0;
}

Neighbours - Adjacency Matrix

int[] getNeighbors(int i){
   if (i <= 0 || i > size)
      throw new IllegalArgumentException("Bad indices.");
   return graph[i-1];
}

Adjacency - Adjacency Matrix

public boolean adjacent(int i, int j){
   if (i <= 0 || i > size || j <= 0 || j > size)
      throw new IllegalArgumentException("Bad indices.");
   return (graph[i-1][j-1] == 1);
}

Graph ADT - Memory and Time Complexity

• Memory = 𝑂(𝑁²) for graphs with 𝑁 nodes and 𝐸 edges (memory-inefficient)

• Worst-case time complexity:

  • Adding node is 𝑂(𝑁²)

  • Removing node is 𝑂(𝑁²)

  • Adding and removing an edge is 𝑂(1) 

  • Adjacency check is 𝑂(1)

Graph Traversals

• Say you want to discover whether from a specific (source) node 𝑠:

  • Another specific node 𝑣 is reachable from 𝑠, and what is the shortest path from 𝑠 to 𝑣

  • Or which nodes are reachable from 𝑠 within some 𝑘 hops

• How do we solve? We traverse the graph using:

  • Depth-First Search

  • Breadth-First Search

  • Etc..

• We went over these traversals previously, but only for trees. Now we need to deal with cycles and loops

Depth-First Search (DFS) Traversal

1. Start at the source, and visit a neighbour (and mark it as visited)

2. From that neighbour, visit one of its neighbours

3. Repeat until you hit an already visited node

4. At which point, you backtrack (i.e., go back), and visit another neighbour instead

5. Until you go back to the source

DFS Code

import java.util.LinkedList;
import java.util.Queue;
import java.util.Stack;

public class GraphSearch{
   boolean[] visitedNodes;
   GraphMatrix graph;
   int graphSize;

   public GraphSearch(GraphMatrix g){
      this.graph = g;
      this.graphSize = g.graph.length;
      this.visitedNodes = new boolean[graphSize];
   }

   public LinkedList<Integer> DFS_traverse(int source){
      Stack<Integer> stack = new Stack<Integer>();
      LinkedList<Integer> traversal = new LinkedList<Integer>();
      stack.push(source);
      visitedNodes[source-1] = true;
      while(stack.size() > 0){
         int currentVisitedNode = stack.pop();
         traversal.add(currentVisitedNode);
         for (int i = graphSize-1; i >= 0; i--) {
            if (graph.graph[currentVisitedNode-1][i] == 1
 && ! visitedNodes[i]){
               visitedNodes[i] = true;
               stack.push(i+1);
            }
         }
      }
      return traversal;
   }
}

DFS Recursive Code

public LinkedList<Integer> DFS_traverse_recursive(int source){
   LinkedList<Integer> traversal = new LinkedList<Integer>();
   visitedNodes[source-1] = true;
   return DFS_traverse_recursive_aux(source, traversal);
}
private LinkedList<Integer> DFS_traverse_recursive_aux(int currentNode, LinkedList traversal){
   traversal.add(currentNode);
   for (int i = 0; i < graphSize; i++) {
      if (graph.graph[currentNode-1][i] == 1
 && ! visitedNodes[i]){
         visitedNodes[i] = true;
         DFS_traverse_recursive_aux(i+1, traversal);
      }
   }
   return traversal;
}

Breadth-First Search (BFS) Traversal

1. Start at the source, and visit all nodes at distance 1, then all nodes at distance 2, …

2. When done, the traversed edges form a BFS tree

3. The BFS tree gives the shortest paths from 𝒔 (if no edge weights)

BFS Code

import java.util.LinkedList;
import java.util.Queue;
import java.util.Stack;

public class GraphSearch{
   boolean[] visitedNodes;
   GraphMatrix graph;
   int graphSize;

   public GraphSearch(GraphMatrix g){
      this.graph = g;
      this.graphSize = g.graph.length;
      this.visitedNodes = new boolean[graphSize];
   }

public LinkedList<Integer> BFS_traverse(int source){
   Queue<Integer> queue = new LinkedList<Integer>();
   LinkedList<Integer> traversal = new LinkedList<Integer>();
   queue.add(source);
   traversal.add(source);
   visitedNodes[source-1] = true;
   while(queue.size() > 0){
      int currentVisitedNode = queue.remove();
      for (int i = 0; i < graphSize; i++) {
         if (graph.graph[currentVisitedNode-1][i] == 1
&& ! visitedNodes[i]){
            traversal.add(i+1);
            visitedNodes[i] = true;
            queue.add(i+1);
         }
      }
   }
   return traversal;
}