H2 - Exploratory Data Analysis (EDA)

Wat is EDA

Critical first step in analysing data
People are not very good at looking a columns of numbers / spreadsheets and determining important characteristics of data

EDA allows to

• Visualise distributions and relationships

• Detect mistakes

• Check assumptions

EDA methods

• Ordering: Stem-and-leaf plots

• Grouping: frequency displays, distributions, histograms

• Summaries: summary statistics, standard deviation, box-and-whisker plots

Classificatie van EDA

• 2 soorten

Graphical or non-graphical methods

1. Non-graphical: calculation of summary statistics

2. Graphical: summarize data in a diagrammatic or pictorial way

Univariate or multivariate

1. Univariate: investigate one variable (data column) at a time

2. Multivariate: investigate two or more variables at a time to explore relationships (typically bivariate)

Almost always a good idea to perform univariate EDA on each of the components of a multivariate EDA before performing multivariate EDA

Univariate Non-Graphical EDA: Data

• categorical data

• quantitative data

• frequency distribution tables

For categorical data: range of values and frequency (or relative frequency) of occurrence for each value are of interest

• Tabulation of frequency is the best univariate non-graphical EDA for categorical data

Univariate EDA for a quantitative variable is a way to make preliminary assessments about the population distribution of the variable
Noteworthy characteristics:

• Central tendency

• Spread

• Modality (number of peaks)

• Shape (heaviness of the tails)

• Outliers

Frequency distribution table

• Shows number of observations for each range of data

• Intervals can be chosen

Cumulative frequency distribution table

• Show frequency, relative frequency and cumulative frequency of the observations

Univariate Non-Graphical EDA: Central tendency

• mean, median & mode (3)

• EX vraag vorig jaar mode

Median

• If there are an even number of observations take the average of the two middle values

• Median is considered a better measure of central tendency than mean for skewed distributions

  • E.g. median income of US families is $43.318, while mean is $60.828 (US census Bureau 2004)

Mode is more helpful for categorical data

• Unimodal: single peak in distribution vs bimodal / multi-modal (two or more peaks)

• Symmetric distributions: mode = mean = median

• Skewed distributions: mode is on the other side of the median from the mean (see examples later on)

Univariate Non-Graphical EDA: Spread

• Range

• Sample variance (s²)

• sample standard deviation (s)

• quartiles (ex)

Spread is an indicator how far away from the center we are still likely to find data values

Range
Range = max-min
Difference between maximum and minimum values
-> Not a robust measure of spread: outliers heavily influence range

Sample Variance
Calculated for a list of numbers (n observations labelled x1 to xn) based on their deviation from the mean

Sample variance = mean of the squares of the individual deviations

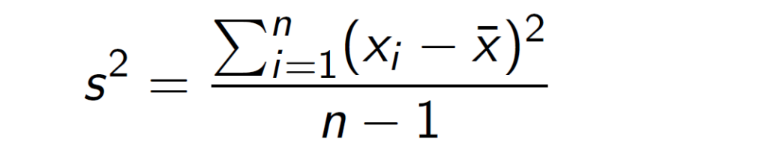
The bigger the deviations from the mean, the bigger the variance
Fairly robust measure of spread

Sample Standard Deviation
Sample standard deviation = square root of the sample variance

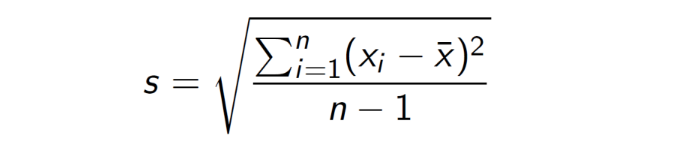
Interpretation: sample standard deviation gives an idea of how much observations differ from the mean

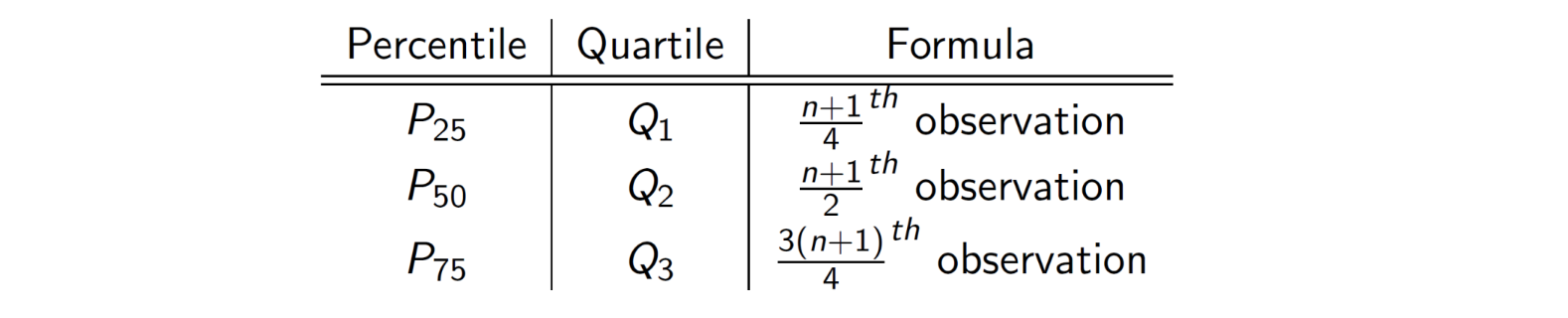
Quartiles

Quartiles are the three values which divide the observed data into even fourths

• One quarter of the data fall below the first quartile (Q1)

• One half fall below the second quartile (Q2) = median

• Three fourths fall below the third quartile (Q3)

Q1 = median of lower half of data
Q2 = median
Q3 = median of upper half of data

IQR = Interquartile range = Q3 – Q1

• Contains 50% of data

• If IQR is high the data is more spread out

• Extreme outliers have little or no effect on the IQR

• Robust measure of spread

The rth percentile, Pr

• Value that is greater than or equal to r percent of data samples

• Or less than or equal to (100 - r) percent of the data samples

  

Univariate Non-Graphical EDA: Stem-and-leaf plots

Substitute for histogram (see graphical EDA)

• Easier to make by hand

• Shows all data values and the shape of the distribution

Univariate Graphical EDA:

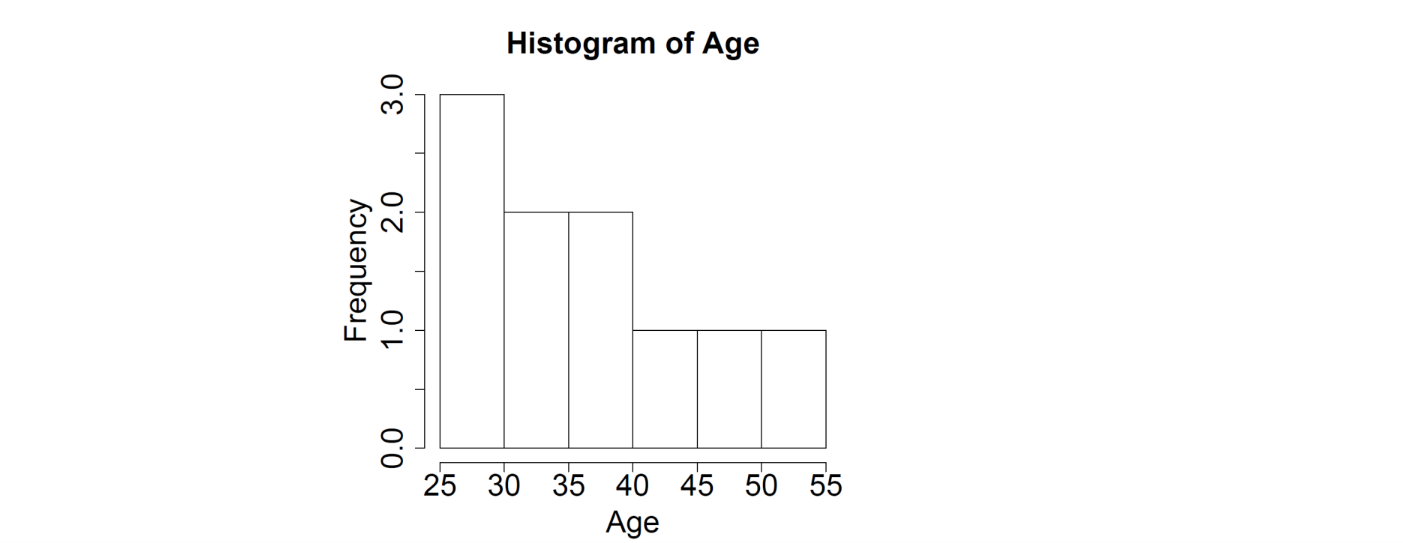
• Histogram

• boxplots (EX)

Histograms
Graphs are generally better to use in presentations than tables as they allow rapid identification of a trend

Histogram = barplot of frequency or relative frequency distribution

Boxplot / Box-and-whisker plots display

• Upper hinge = Q3 = third quartile

• Lower hinge = Q1 = first quartile

• Interquartile range (IQR) = Q3 - Q1

  • Contains middle 50% of data

• Upper fence: upper hinge + 1.5*(IQR)

• Lower fence: lower hinge – 1.5*(IQR)

• Outliers: data values beyond the fences, typically individually plotted

Lower and upper whisker ends are drawn to the smallest and largest observations within the fences
Boxplots provide robust measures of center and spread as well as providing information about symmetry and outliers

Multi-Variate Non-Graphical EDA:

• 2 categorical variables

• 1 categorical and 1 quantitative variable

• 2 quantitative variables (EX)

2 Categorical Variables
frequency table

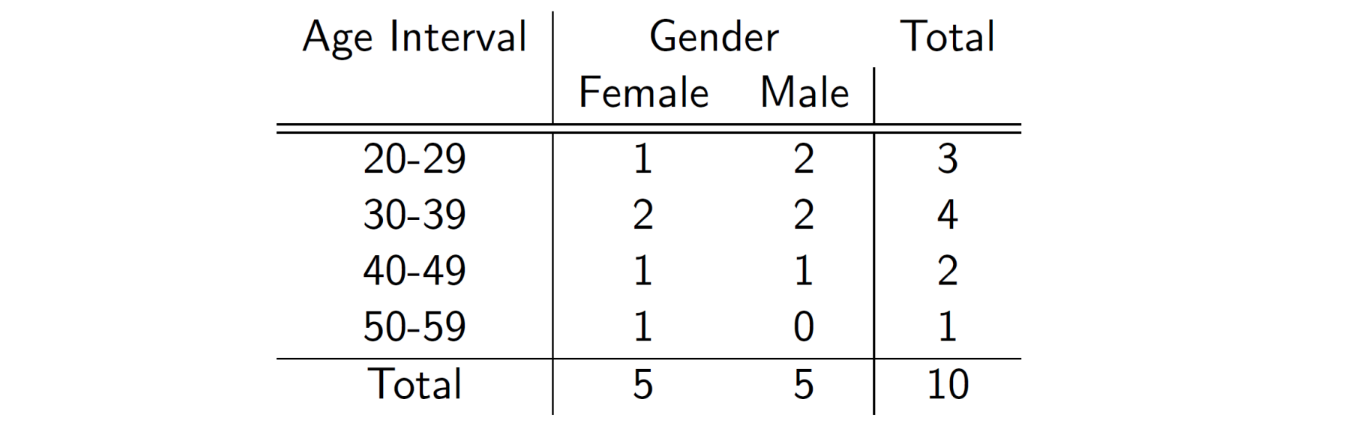
1 Categorical And 1 Quantitative Variable
Stratified stem-and-leaf plots

2 Quantitative Variables
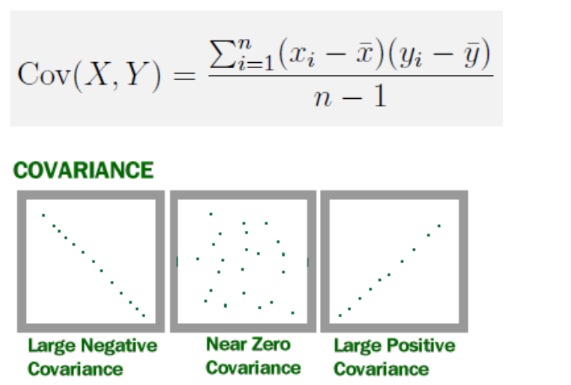
Basic statistics of interest
-> belangrijkste hiervan wat betekent covariance en correlation nu eig?

• Covariantie meet de richting van het lineaire verband tussen twee variabelen.

  • Positieve covariantie: als de ene variabele toeneemt, neigt de andere ook toe te nemen.

  • Negatieve covariantie: als de ene toeneemt, neigt de andere af te nemen.

  • Nabij nul: weinig tot geen lineair verband.

  

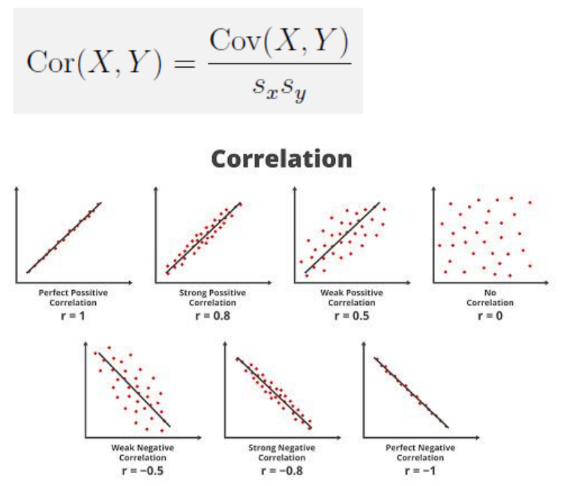
• Correlatie meet zowel de richting als de sterkte van het lineaire verband tussen twee variabelen, en is geschaald tussen -1 en +1.

  • +1: perfecte positieve correlatie

  • -1: perfecte negatieve correlatie

  • 0: geen lineair verband

  

Multi-Variate Graphical EDA:

• 1 Categorical And 1 Quantitative Variable

• 2 Quantitative Variables

• Common Distribution Shapes (EX)

1 Categorical And 1 Quantitative Variable
Side-by-side box plots
Allows to compare the distribution of the continuous variable (age) across values of the categorical variable (gender)

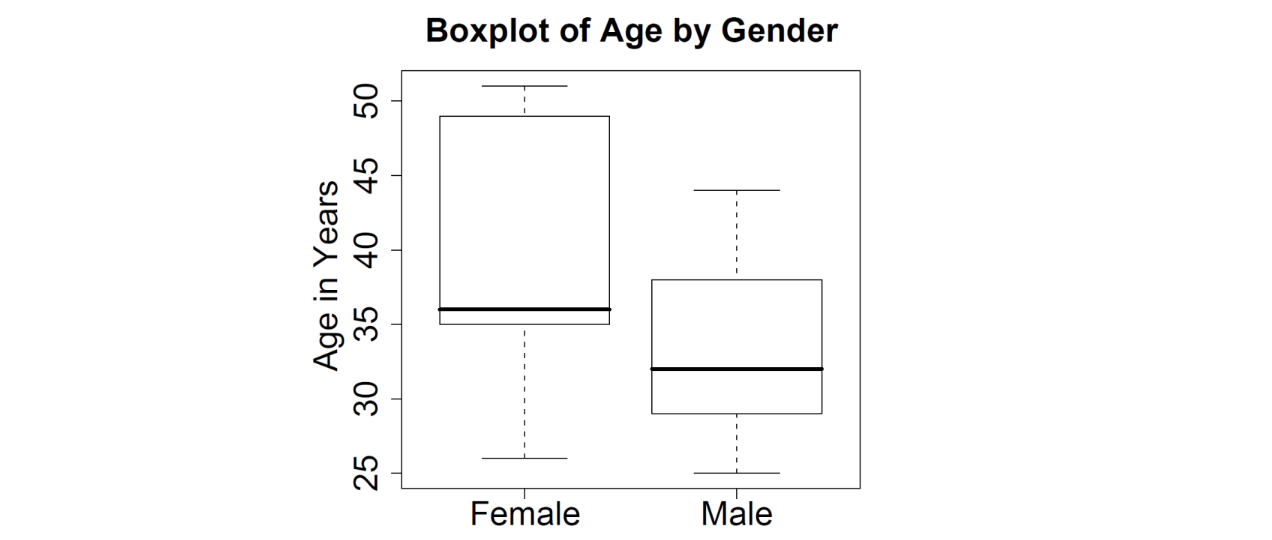
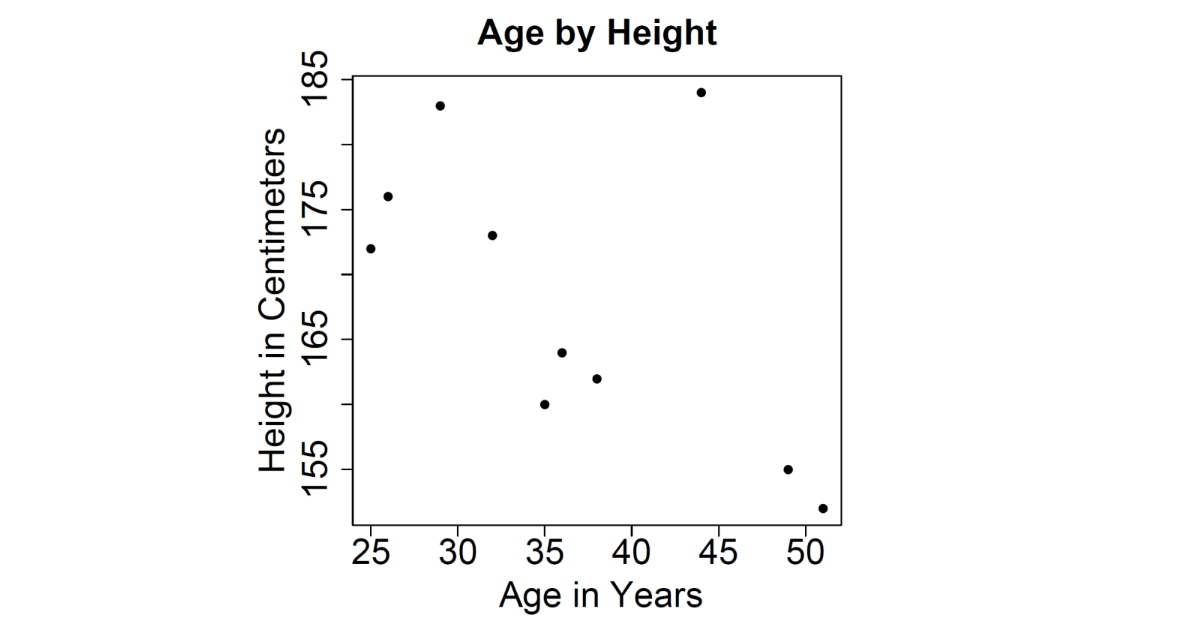
2 Quantitative Variables
Scatterplot: Visually display the relationship between two continuous variables

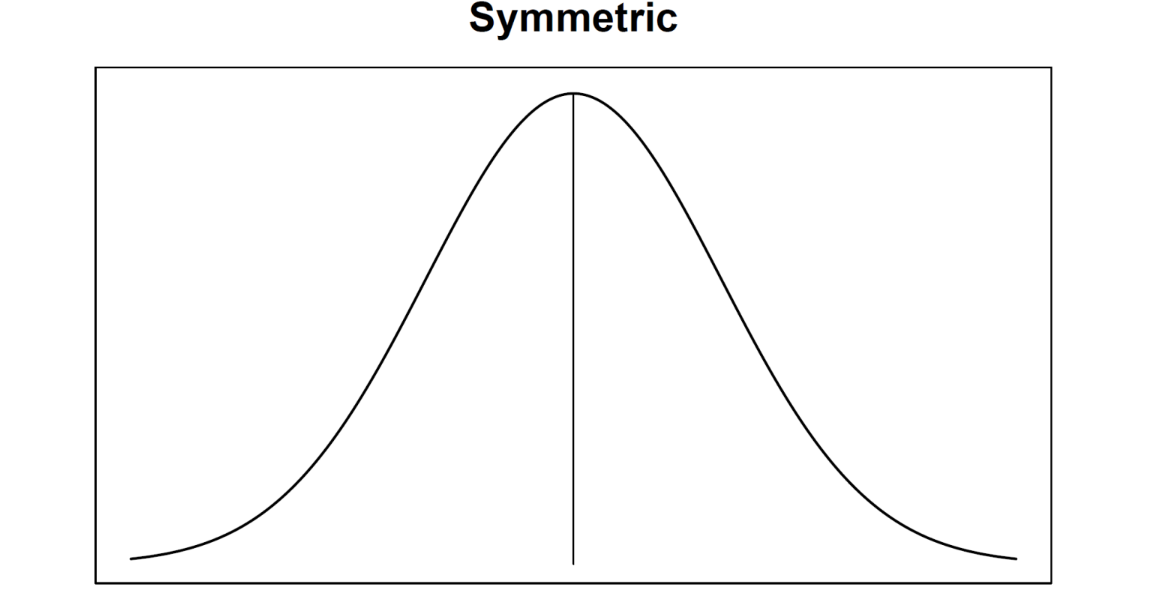
Common Distribution Shapes

Symmetric distribution

• Left tail looks like right tail (mirrored)

• Mean = Median = Mode

  

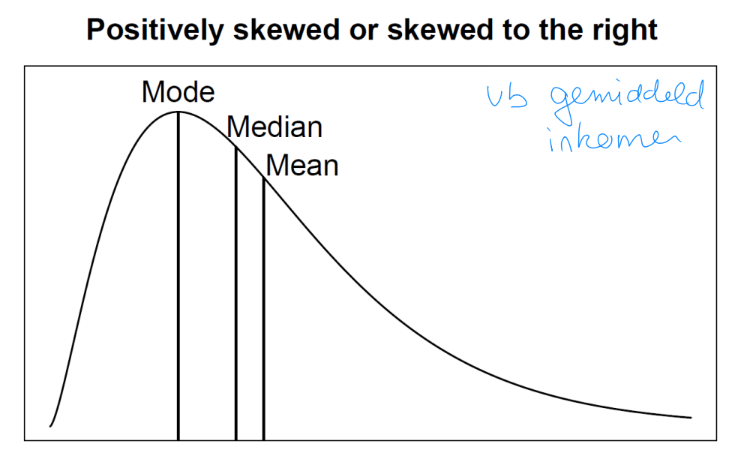
Positively skewed

• Longer tail in the high values

• Mean > Median > Mode

  

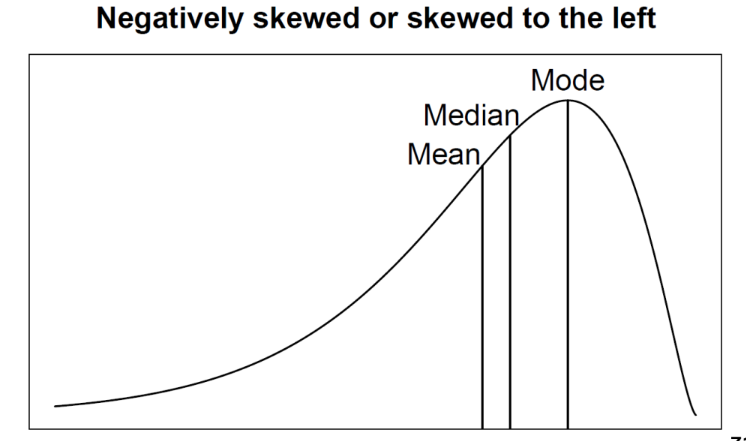
Negatively skewed

• longer tail in the low values

• Modes > Median > Mean