AP stats General Multiplication Rule

0.0(0)
studied byStudied by 0 people
learnLearn
examPractice Test
spaced repetitionSpaced Repetition
heart puzzleMatch
flashcardsFlashcards
Card Sorting

1/6

encourage image

There's no tags or description

Looks like no tags are added yet.

Study Analytics
Name
Mastery
Learn
Test
Matching
Spaced

No study sessions yet.

7 Terms

1
New cards

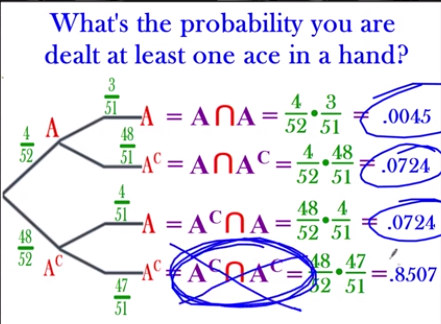
In Texas Hold’em poker, two cards are death to each player. The best staring hand is two aces. Draw a tree diagram showing all the possibilities of getting Aces vs no aces for each card dealt.

One branch, then 2 branches stemming from each

2
New cards

Let’s formalize all of the probabilities we see per branch

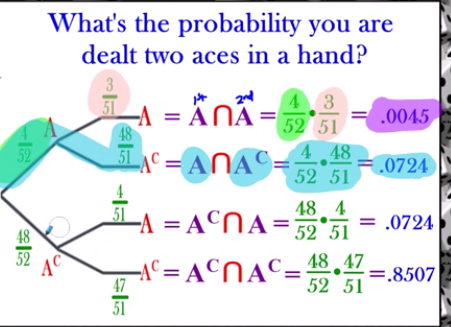
P(A)→ A= P(2ndA | 1stA) + Ac = P(2ndAc | 1stA)

P(Ac)→ A= P(2ndA | 1ndAc) + Ac = P(2nd Ac | 1stAc)

the entirety of 2nd branches are all conditional probabilities

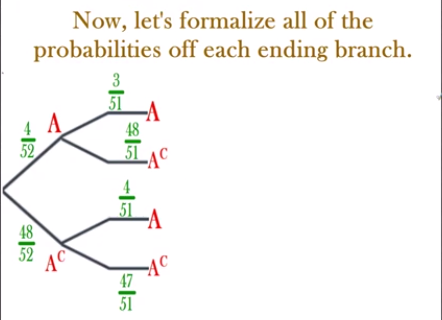
<p>P(A)→ A=<strong> P(<sup>2nd</sup>A | <sup>1st</sup>A) </strong>+ A<sup>c</sup> = <strong>P(<sup>2nd</sup>A<sup>c</sup> | <sup>1st</sup>A)</strong></p><p>P(A<sup>c</sup>)→ A= <strong>P(<sup>2nd</sup>A | <sup>1nd</sup>A<sup>c</sup>) </strong>+ A<sup>c</sup> = <strong>P(<sup>2nd</sup> A<sup>c</sup> | <sup>1st</sup>A<sup>c</sup>)</strong></p><p><strong>the entirety of 2nd branches are all conditional probabilities</strong></p>
3
New cards
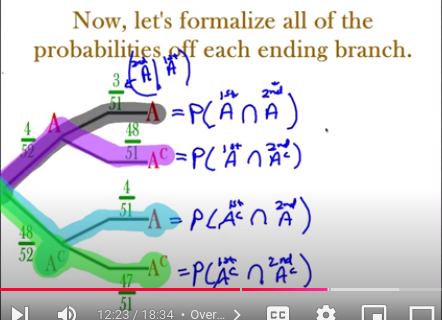
<p><strong>1st</strong> , <span style="color: purple"><strong>2nd branches, </strong></span><span style="color: blue"><strong>3rd branch, </strong></span><span style="color: green"><strong>4th branch</strong></span></p>

1st , 2nd branches, 3rd branch, 4th branch

A → A = P(1stA ∩ 2ndA)

A →Ac= P(1stA ∩ 2ndAc)

Ac → A = P(2ndAc ∩ 2ndA)

Ac → Ac = P(1st Ac ∩ 2ndAc)

<p><strong>A → A = P(<sup>1st</sup>A </strong><span><strong>∩ <sup>2nd</sup>A)</strong></span></p><p><span style="color: purple"><strong>A →A<sup>c</sup>= P(<sup>1st</sup>A ∩ <sup>2nd</sup>A<sup>c</sup>)</strong></span></p><p><span style="color: blue"><strong>A<sup>c</sup> → A = P(<sup>2nd</sup>A<sup>c</sup> ∩ <sup>2nd</sup>A)</strong></span></p><p><span style="color: green"><strong>A<sup>c</sup> → A<sup>c</sup> = P(<sup>1st</sup> A<sup>c</sup> ∩ <sup>2nd</sup>A<sup>c</sup>)</strong></span></p>
4
New cards

General Multiplication Rule

P(A and B)

= P(A) times P(B | A)

5
New cards

What’s the probability you are dealt two aces in a hand?

Multiply very first branch to the 2nd one for each (4x)

<p>Multiply very first branch to the 2nd one for each (4x)</p>
6
New cards
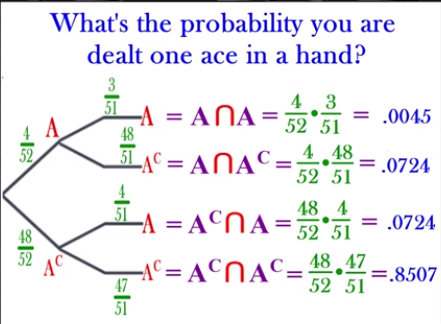
<p>What’s the probability you are dealt <strong>one</strong> ace in a hand?</p>

What’s the probability you are dealt one ace in a hand?

Which event represents getting 1 Ace?

A ∩ A NO! → 2 aces

A ∩ Ac YES! → 1 ace

Ac ∩ A YES! → 1 ace

Ac ∩ Ac NO! → no aces

Add the Yes events,

0.724 + 0.724 = .1448

<p>Which event represents getting 1 Ace?</p><p>A <span>∩ A NO! → 2 aces</span></p><p><span style="color: #00ff02">A ∩ A<sup>c</sup> YES! → 1 ace</span></p><p><span style="color: #00ff02">A<sup>c</sup> ∩ A YES! → 1 ace</span></p><p><span>A<sup>c </sup>∩ A<sup>c</sup> NO! → no aces</span></p><p><span>Add the Yes events, </span></p><p><span>0.724 + 0.724 =<strong> .1448</strong></span></p>
7
New cards

What’s the probability you are dealt at one ace in a hand?

Choose the events that have at least 1 ace

A ∩ A YES! → 2 aces

A ∩ Ac YES! → 1 ace

Ac ∩ A YES! → 1 ace

Ac ∩ Ac NO! → no aces

I could either add up all values, or just subtract from the one that isn’t valid by 1

1 - .8507 = .1493

<p>Choose the events that have at least 1 ace</p><p><span style="color: #00ff02">A ∩ A YES! → 2 aces</span></p><p><span style="color: #00ff02">A </span><span style="color: #00ff02">∩ A<sup>c</sup> YES! → 1 ace</span></p><p><span style="color: #00ff02">A<sup>c</sup> ∩ A YES! → 1 ace</span></p><p><span>A<sup>c</sup> ∩ A<sup>c</sup> NO! → no aces</span></p><p><span>I could either add up all values, or just subtract from the one that isn’t valid by 1</span></p><p><span>1 - .8507 = <strong>.1493</strong></span></p>

Explore top notes

Explore top flashcards