Grade 10 review

started at page 566

The parabola y=x² are given. State the new coordinates under each transformation

a) (2,4); shift up 3

b) (-2,4); shift down 5

c) (-1,1); shift left 4

d) (1,1); shift right 6

e) (3,9); vertical stretch of -1/3

f) (2,4); vertical stretch of 2

a) (2,7)

b) (-2, -1)

c) (-5, 1)

d) (7, 1)

e) (3, -3)

f) (2, 8)

The parabola y=x² are given. State the new coordinates under each transformation

a) (-2, 4); shift left 2 and up 5

b) (-1, 1); shift right 4, vertical stretch 3, and reflect about x-axis

c) (3, 9); vertical compression by 3, shift left 5, and shift down 2

d) (0, 0); shift left 5, vertical stretch 3, shift up 4, and reflect about x-axis

a) (-4, 9)

b) (3, -3)

c) (-2, 1)

d) (-5, -4)

Points (-2, 4), (0, 0), and (2, 4) are on the parabola y = x². Use your knowledge of transformations to determine the equation of the parabola using these coordinates.

a) (-2, 6), (0, 2), (2, 6)

b) (-2, 12), (0, 0), (2, 12)

c) (2, 4), (4, 0), (6, 4)

d) (-2, -6), (0, -2), (2, -6)

a) y = x² + 2

b) y = 3x²

c) y = (x - 4)²

d) y = -x² - 1

Sketch each graph using transformation on y = x²

a) y = +x²

b) y = -x²

c) y = (x - 3)²

d) y = (x + 4)²

e) y = 2x²

f) y = 1/2 x²

look at page 566 question 4

Sketch each graph using transformation on y = x²

a) y = 2(x - 1)²

b) y = -3(x + 1)²

c) y = 1/2(x - 2)²

d) y = -1/3(x + 2)²

look at page 566 question 5

Write the equation of a circle centered at the origin, with each radius

a) 3

b) 7

c) 8

d) 1

a) x² + y² = 9

b) x² + y² = 49

c) x² + y² = 64

d) x² + y² = 1

What is the radius of the circle with each equation? Round your answer to the nearest hundredth, if necessary.

a) x² + y² = 9

b) x² + y² = 81

c) x² + y² = 15

d) x² + y² = 27

e) x² + y² = 6.25

f) x² + y² = 17.64

a) 3

b) 9

c) 3.87

d) 5.20

e) 2.50

f) 4.20

A point on the circle x² + y² = 169 has an x-coordinate of 12. What are the possible values of the y-coordinate?

y = 5 and y = -5

Plot the circle with the given equation

a) x² + y² = 16

b) x² + y² = 49

c) x² + y² = 100

d) x² + y² = 12.25

look at page 568 question 4

Write each trinomial as a perfect square

a) x² + 2x + 1

b) x² + 4x + 4

c) x² + 6x + 9

d) x² + 10x + 25

pg 564 #1

a) y = (x + 1)²

b) y = (x + 2)²

c) y = (x + 3)²

d) y = (x + 5)²

Complete the square, and write in vertex form

a) y = x² + 2x + 2

b) y = x² + 4x + 6

c) y = x² - 12x + 40

d) y = x² - 18x + 80

pg 564 #2

a) y = (x + 2)² + 1

b) y = (x + 2)² + 2

c) y = (x - 6)² + 4

d) y = (x - 9)² - 1

Express in vertex form by completing the square. State the equation of the axis of symmetry and the coordinates of the vertex.

a) y = 2x² - 4x + 7

b) 5x² + 10x + 6

c) -3x² - 12x + 2

d) -2x² + 6x + 2

pg 564 #3

a) y = 2(x - 1)² + 5 x = 1 (1, 5)

b) y = 5(x + 1)² + 1 x = -1 (-1, 1)

c) y = -3(x + 2)² + 14 x = -2 (-2, 14)

d) y = -2(x - 1.5)² + 6.5 x = 1.5 (1.5, 6.5)

A baseball is hit from a height of 1m. It’s height in metres, h, after t seconds is h = -5t² + 10t + 1

a) What is the maximum height of the ball?

b) When does the ball reach this height?

pg 564 #4

a) 6m

b) 1s

Sketch the graphs, using partial factoring

a) y = 2x² - 6x + 5

b) y = -3x² + 9x - 2

c) y = 5x² - 3 + 5x

d) y = 3 + 4x - 2x²

look at page 563 question 1

Sketch the graphs, using zeros of the curve

a) y = x² + 4x - 12

b) y = x² - 7x + 10

c) y = 2x² - 5x - 3

d) y = 6x² - 13x - 5

look at page 563 question 2

Sketch the graphs

a) y = (x - 2)² + 3

b) y = (x + 4)² - 10

c) y = 2(x - 1)² + 3

d) y = -3(x + 1)² - 4

look at page 563 question 3

Factor each expression

a) 4 - 8x

b) 6x² - 5x

c) 3m²n³ - 9m³n⁴

d) 28x² 14xy

pg 556 #1

a) 4(1 - 2x)

b) x(6x - 5)

c) 3m²n³(1 - 3mn)

d) 14x(2x - y)

Factor each expression

a) x² - x - 6

b) x² + 7x + 10

c) x² - 9x + 20

d) 3y² + 18y + 24

pg 556 #2

a) (x + 2)(x - 3)

b) (x + 2)(x + 5)

c) (x - 5)(x - 4)

d) 3(y + 4)(y + 2)

Factor

a) 6y² -y - 2

b) 12x² + x - 1

c) 5a² + 7a - 6

d) 12x² - 18x - 12

pg 556 #3

a) (3y - 2)(2y + 1)

b) (3x + 1)(4x - 1)

c) (5ax - 3)(a + 2)

d) 6(2x + 1)(x - 2)

Solve

a) (x - 3)(x - 2) = 0

b) (2x - 5)(3x - 1) = 0

c) (m - 4)(m - 3) = 0

d) (3 - 2x)(4 - 3x) = 0

e) (2y + 5)(3y - 7) = 0

f) (5n - 3)(4 - 3n) = 0

pg 558 #1

a) x = 3 x = 2

b) x = 5/2 x = 1/3

c) m = 4 m = 3

d) x = 3/2 m = 4/3

e) y = -5/2 y = 7/3

f) n = 3/5 n = 4/3

Determine the roots

a) x² - x - 2 = 0

b) x² + x - 20 = 0

c) m² + 2m - 15 = 0

d) 6x² - x - 2 = 0

e) 6t² + 5t - 4 = 0

f) 2x² + 4x - 30 = 0

pg 558 #2

a) x = 2 x = -1

b) x = 4 x = -5

c) m = 3 m = -5

d) x = -1/2 x = 2/3

e) t = -4/3 t = 1/2

f) x = 3 x = -5

A model rocket is shot straight into the air. It’s height in meters at t seconds is given by h = -4.9t² + 29.4t. When does the rocket reach the ground?

pg 558 #4

at 6s

Solve

a) 4x² = 8x - 1

b) 4x² = 9

c) 6x² - x = 1

d) 5x² - 6 = -7x

e) 3x² + 5x -1 = 2x² + 6x + 5

f) 7x² + 2(2x + 3) = 2(3x² - 4) + 13x

pg 558 #3

The population of a city is modelled by P = 0.5t² + 10t + 200, where P is the population in thousands and t is the time in years, with t = 0 corresponding to the year 2000. When is the population 350 000?

pg 558 #5

In the year 2010

Go to page 561 # 1 a)

laalal

Go to page 562 b)

Go to page 561 #2

What is a function?

• A function is a special relation.

• It is a set of ordered pairs in which for every value of x, there is only one value of y

What is a relation?

• A relation is a set of ordered pairs

How do you know if a line/graph is a function?

• If there is more than one value of y for an x value then it is not a function

What is the domain and the range?

• Domain are x values

  • The set of first elements in a relation

• Range are y values

  • The set of second value elements in a relation

What is independent variable and dependant variable?

• X is the independent value (domain)

• Y is the dependant value (range)

What is the input and output value?

• X is input (domain)

• Y is output (range)

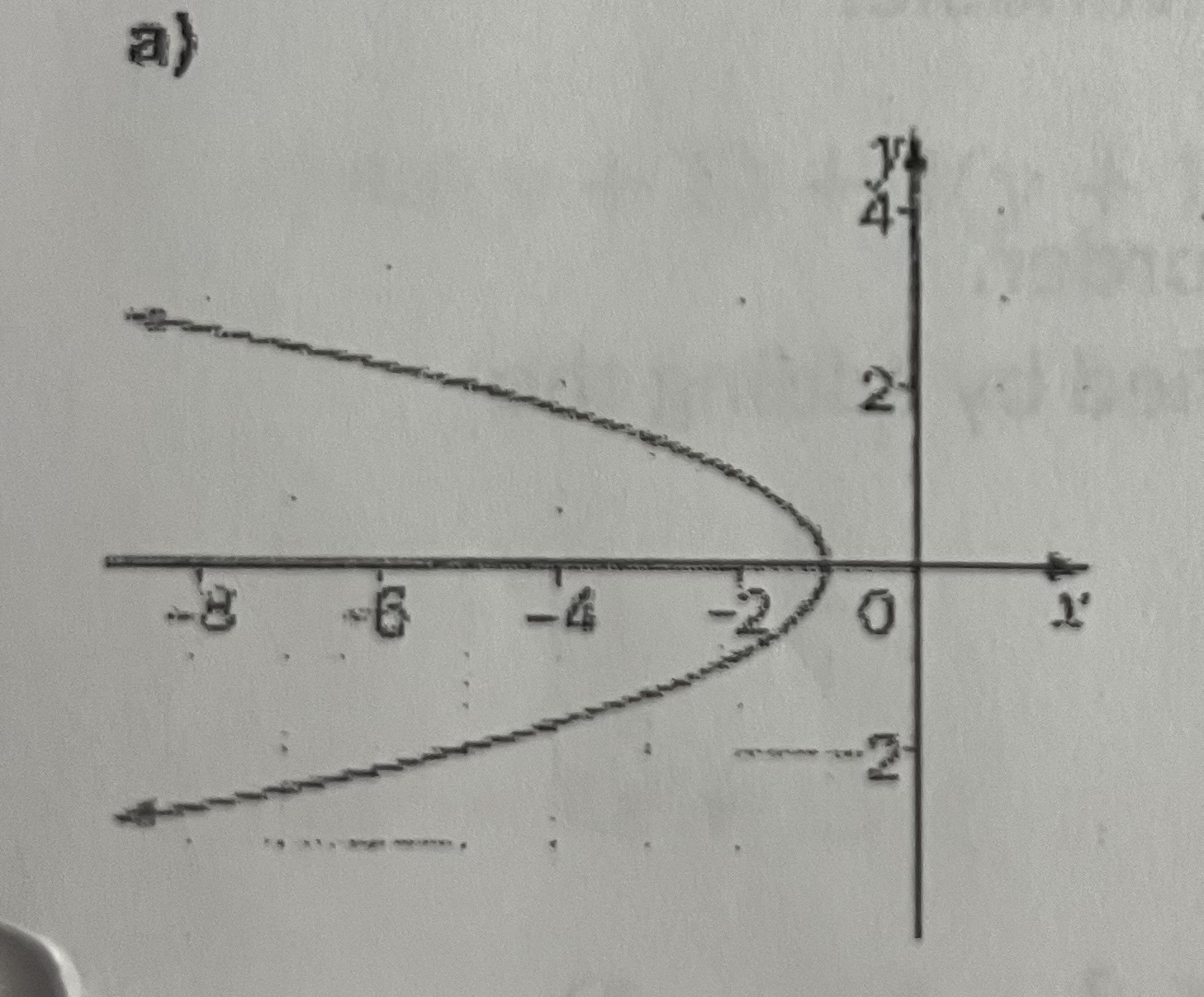
Is this a function? Why?

• No it is not because there are x values with more than one y value

• This is a relation

Is this a function? Why?

• Yes, because for each x value there is one y value

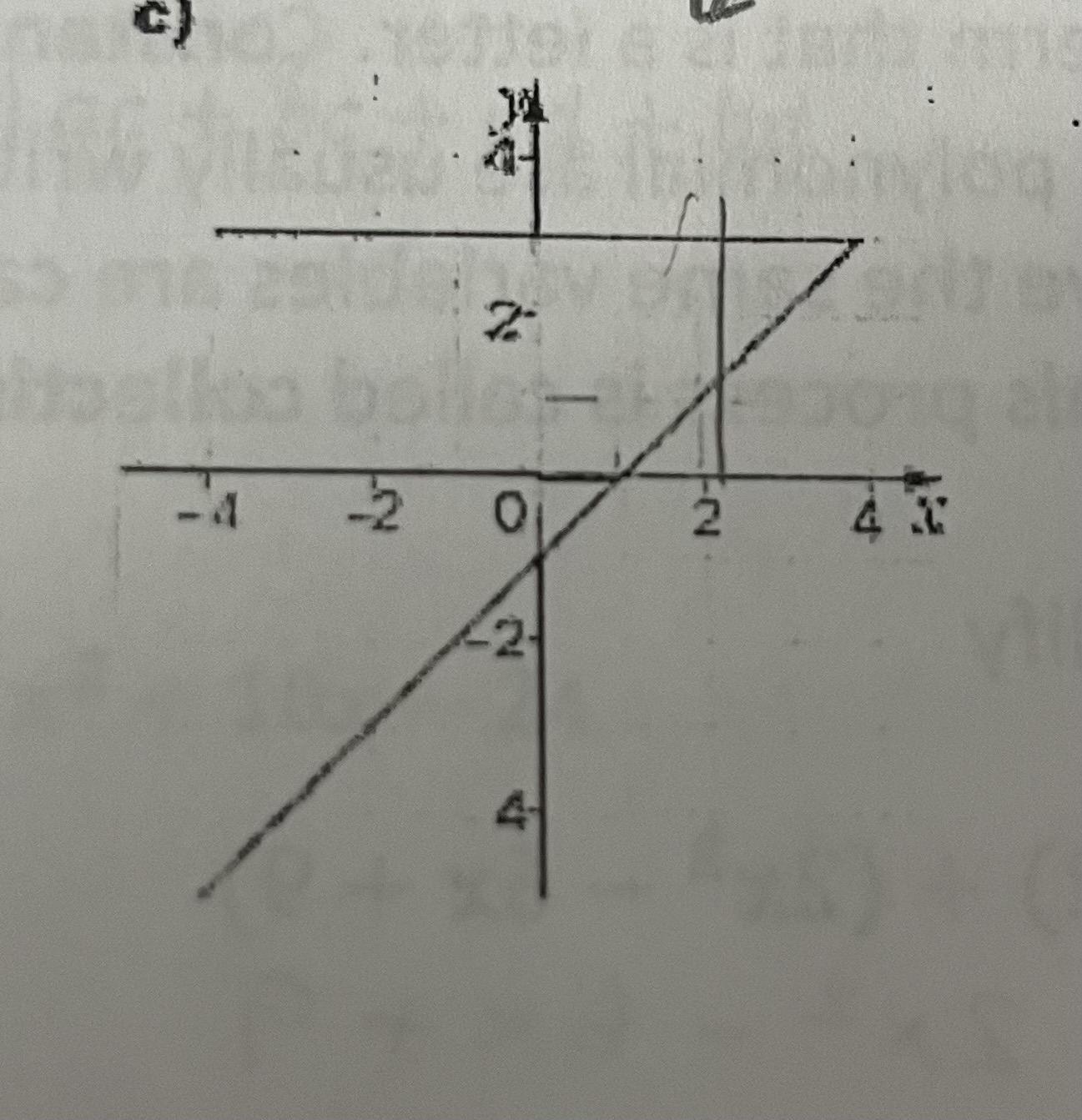
Is this a function? Why

• No it is not because some x values have more than one y value

• This is a relation

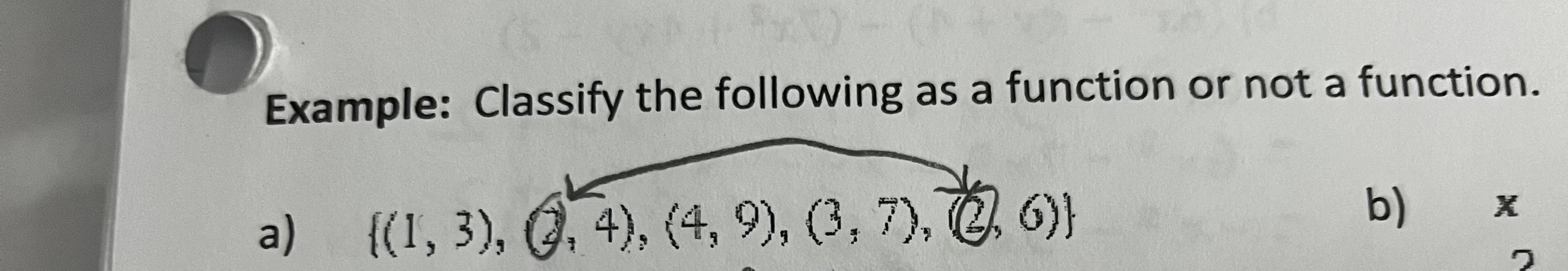
Is this a function? Why?

• No because there are two y outputs for one x input

• This is a relation

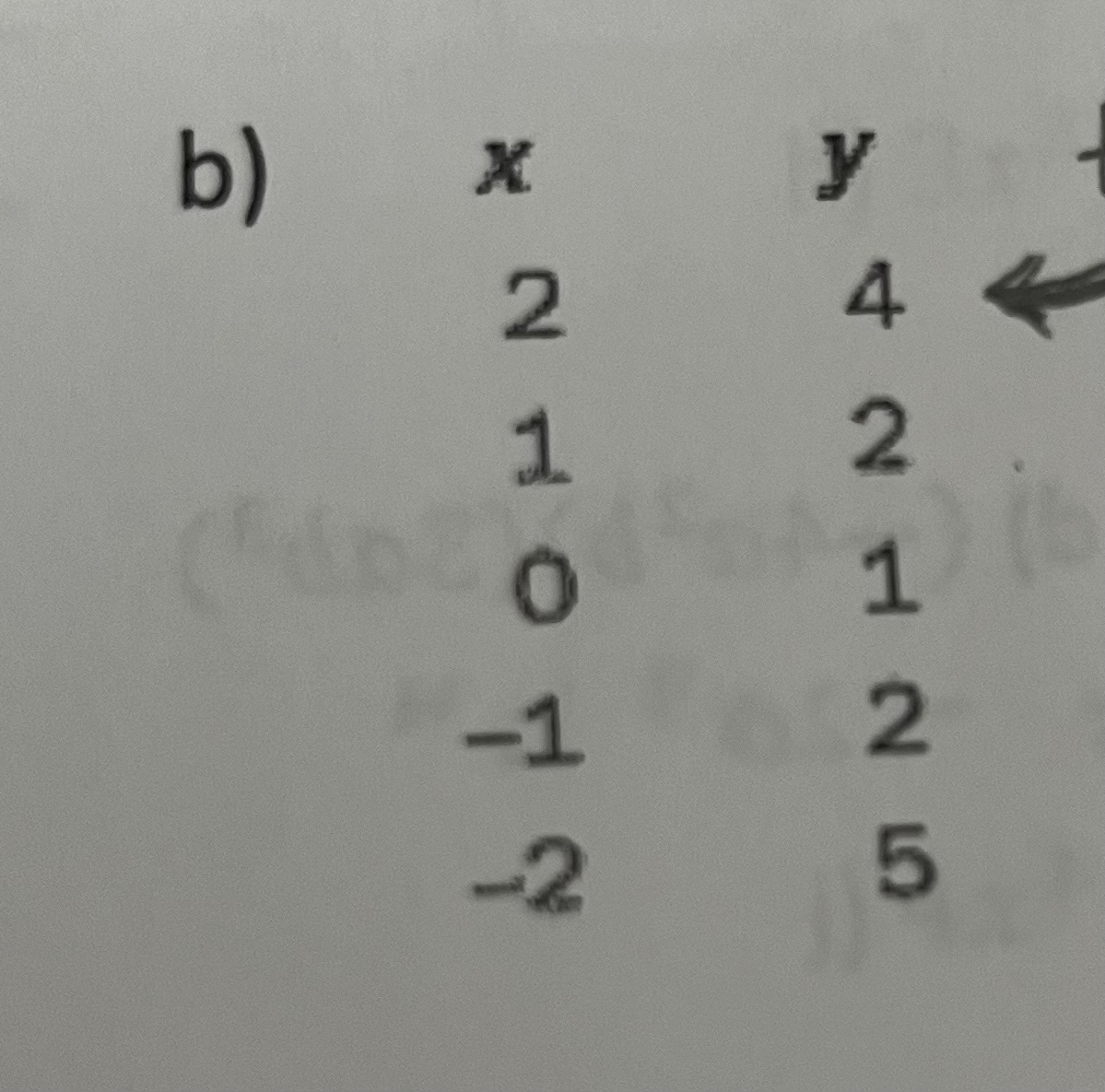
Is this a function? Why?

• Yes because for each input there is one output

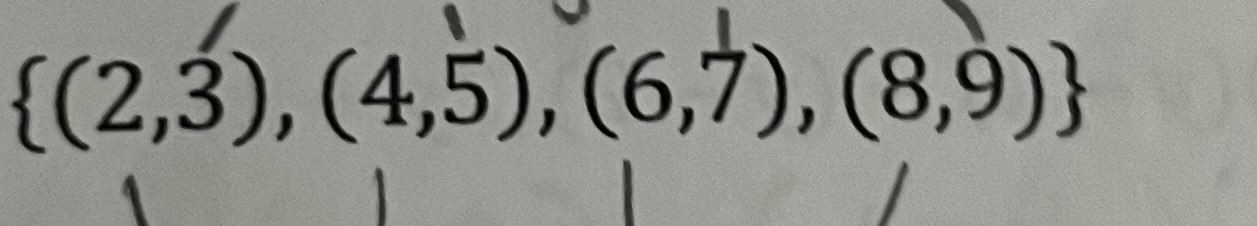
What is the domain and range?

• Domain → {2, 4, 6, 8}

• Range → {3, 5, 7, 9}

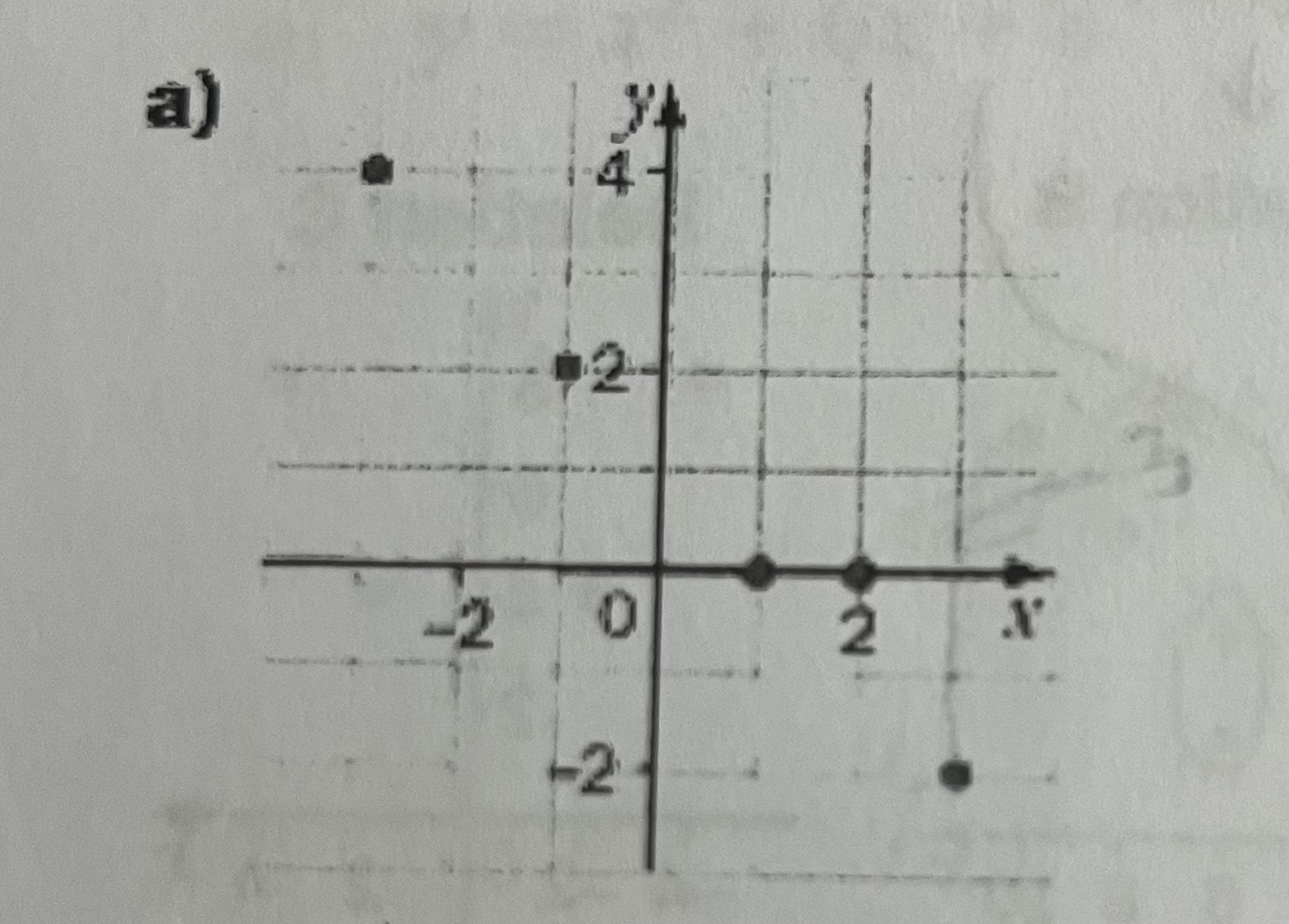
Determine the domain and range for the following

• Domain → {-3, -1, 1, 2, 3}

• Range →{4, 2, 0, -2} (0 don’t repeat)

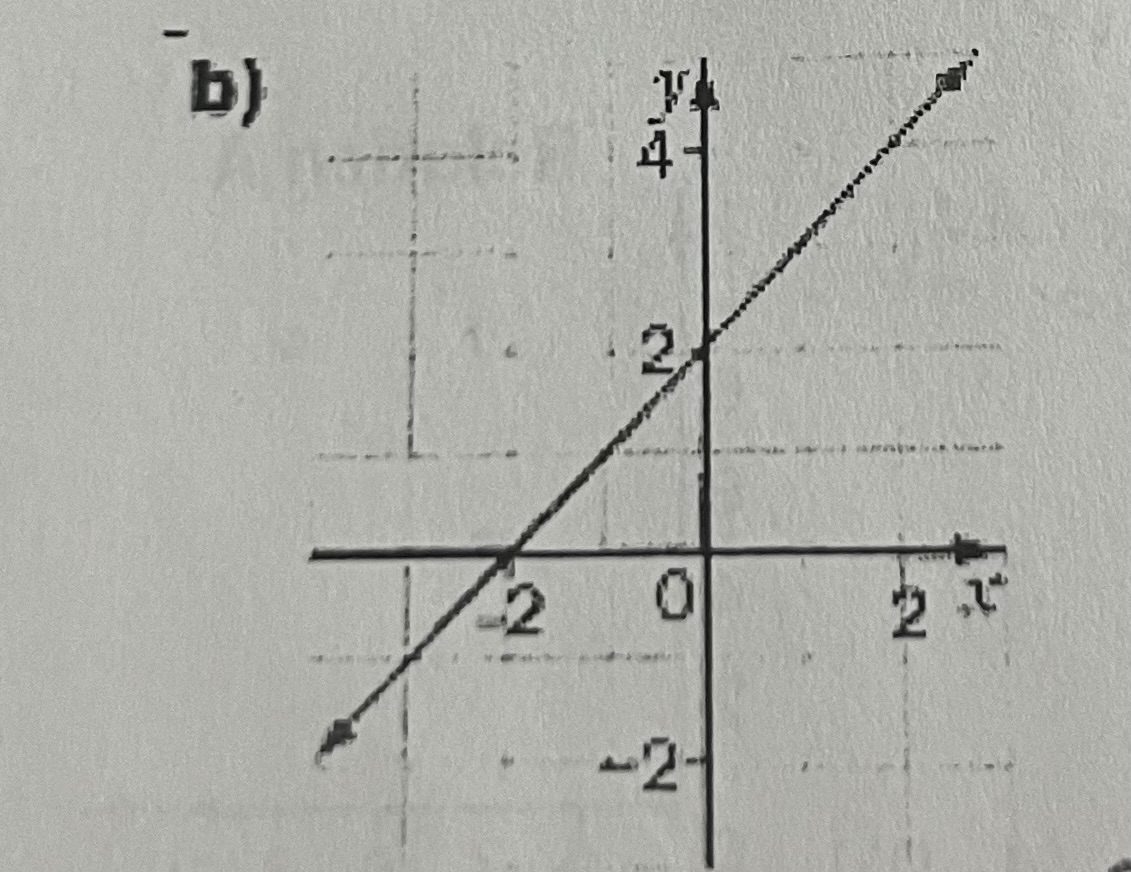
Determine the domain and range for the following

• Domain →{xER} (since there are arrows so x is unlimited)

• Range →{yER}

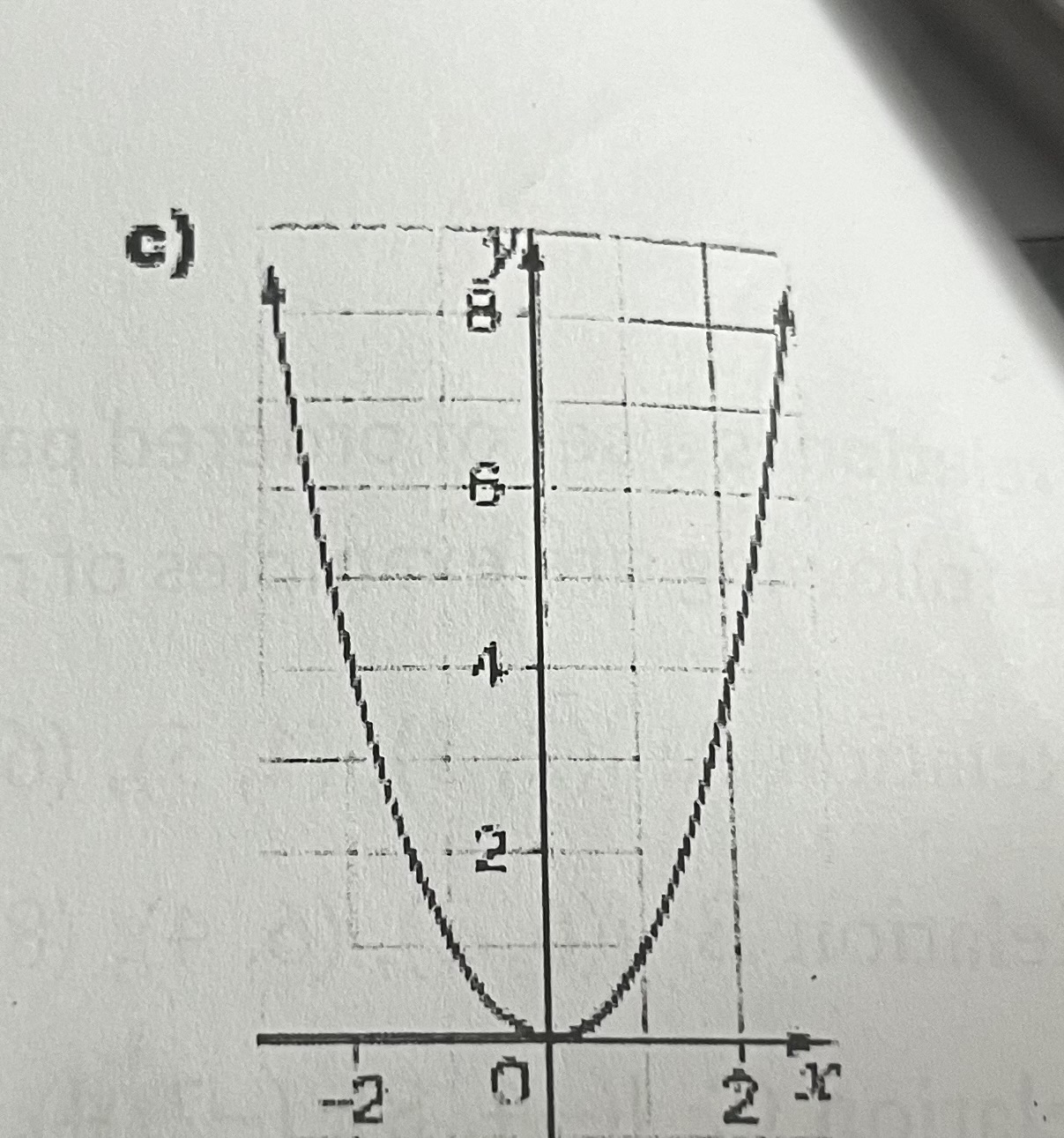
Determine the domain and range for the following

Domain →{xER} (x is unlimited)

Range → {xER | y ≥ 0}

What is a polynomial?

• A polynomial is an algebraic expression formed by adding or subtracting terms.

What is a coefficient

• A coefficient is the number that is in front of a variable

What is a variable

• A variable is a term that is a letter

What is a constant?

• A constant is a term that is a number

Simplify:

a) (x² + 4x - 2) + (2x² - 6x + 9)

b) (6x² - xy + 4) - (7x² + 4xy - 2)

c) (2x²)(7x)

d) (-4a²b)(3ab³)

e) 20x³y⁴/-5x²y²

f) 4(x - 3) - 2x(2x - 1)

g) 3x(x - 2) + 2(2x + 5) - x(3x - 2)

h) (x + 1)(x + 2)

I) 2(3y + 2)(y - 1) - (y - 2)(2y + 1)

a) 3x² - 2x + 7

b) -x² - 5xy + 6

c) 14x³

d) -12a³b⁴

e) -4xy²

f) (-4x²) + 6x - 12

g) 10

h) x² + 2x + x + 2

I) 4y² + y - 2

Factor:

a) 8x³ - 6x²y² + 4x²y

b) 2x⁴ - 4x² - 6x

c) 4x(y + 1) + 3(y + 1)

d) ac + bc + ad + bd

e) x² - 8x + 12

f) x² + 10x - 24

g) x² - 2xy - 15y²

h) 3x² + 3x - 18

I) 6x² + 13x - 5

j) 4x² - 5x - 6

k) x² - 9

l) 4x² - 1

m) x² + 10x + 25

n) x² - 14x + 49

a) 2x²(4x - 3y² + 2y)

b) 2x(x³ - 2x - 3)

c)(y + 1)(4x + 3)

d) (a + b)(c + d)

e) (x - 2)(x - 6)

f) (x + 12)(x - 2)

g) (x + 3y)(x - 5y)

h) 3(x + 3)(x - 2)

I) (3x - 1)(2x + 5)

j)(x - 2)(4x + 3)

k) (x + 3)(x -3)

l) (2x + 1)(2x - 1)

m)(x + 5)²

n) (x - 7)²