2.2 Graphs of Equations

graph of an equation

the set of all points (x, y) that are solutions of the equation, that make the equation true

finding points to graph an equation

1. solve for y in terms of x (like y=2x)

2. pick some values of x (0, -1, 1, 2, -2, etc) and plug them in to find corresponding y points

2a. make a little table to keep track of the points

2b. plot at least 5 points

3. plot the point pairs and draw a line to connect them

y-x^2=1 sketch the graph

check your answer in desmos, etc.

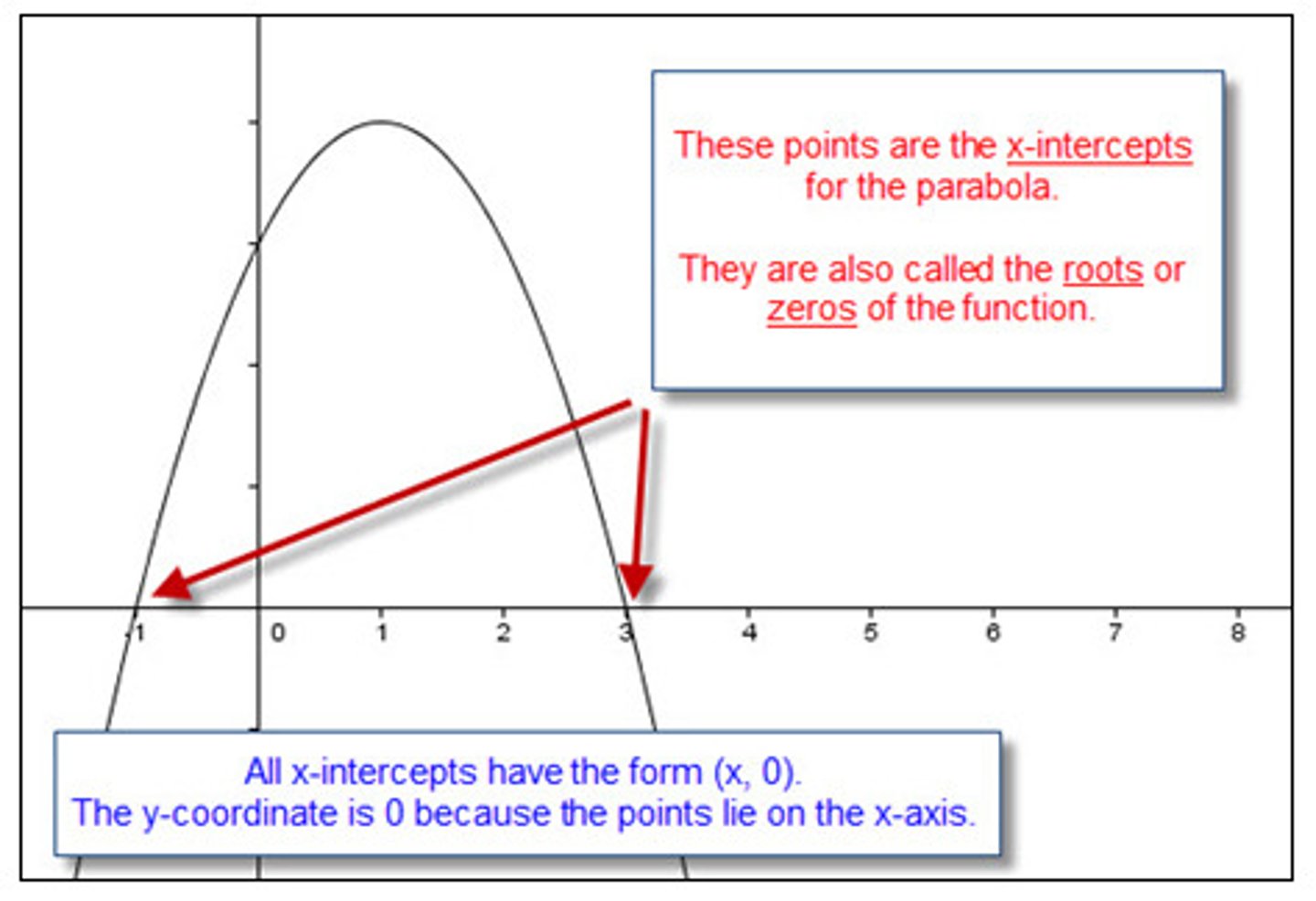
finding x and y intercepts

x: where a function crosses the x-axis. Y-coordinate is 0.

y: where function crosses the y-axis. X-coordinate is 0.

circle on cartesian plane

has a center (h, k) and radius r. is the set of all points (x,y) that are a distance r from (h, k)

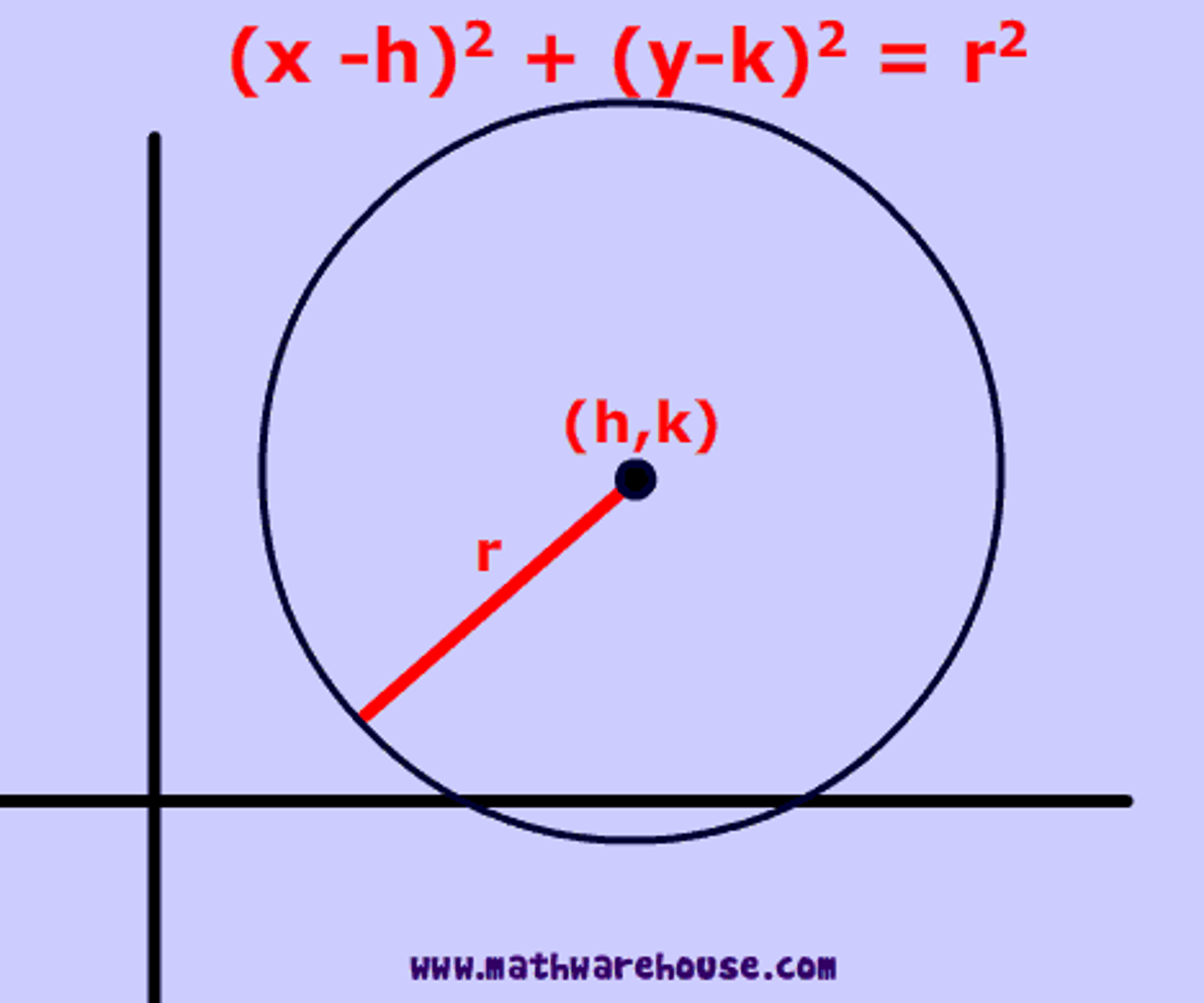
circle equation (standard form)

(x-h)² + (y-k)² = r² where (h,k) is the center and r is the radius

is derived from distance formula

can the radius of a circle be negative?

NO, never. distance from a point is always positive

a circle with center (7, -3) passes through (5, -2). find its equation in standard form.

1. get the distance between the points for the radius.

2. use the center to then plug those values into the equation of a circle

(x-7)^2+(y+3)^3=5

radius and diameter

Radius is half the diameter r=.5d

find the center and radius of x^2+y^2-6x+8y+10=0

1. we basically want to put into standard form

2. use completing the square (x^2-6x __) + (y^2+8y __)=-10

3. find the missing __ value and add to right hand side aswell (x^2-6x+9)+(y^2+8y+16)=-10+9+16

4. using perfect square, simplifly the right hand side to get find formula

(x-3)^2+(y+4)^2=15

center: (3, -4)

radius: sqrt(15)