AP Stats Unit 4: Collecting Data - Terms & Methods

Corresponds to AP Stats Unit 3

bias

when the calculated value from the sample is CONSISTENTLY an over- or underestimate of the true value of the population

• low bias = high accuracy

• high bias = low accuracy

accuracy

when the calculated value from the sample (the mean, etc) is close to the true value of the population

• high accuracy = low bias

• low accuracy = high bias

variability

when the calculated values from the sample are CONSISTENTLY scattered/can be at extremes and far away from each other

or, low variability = when calculated values are CONSISTENTLY CLOSE to each other

*does not imply that they have to be close or far from the true value of the population; that’s bias

• low variability = high precision

• high variability = low precision

precision

when the calculated values from the sample are CONSISTENTLY close to each other

• high precision = low variability

• low precision = high variability

census

a survey of the ENTIRE population; usually not feasible, and samples are preferred

simple random sample (SRS)

sampling method where choosing every individual AND group of individuals is equally likely to occur

• LOW BIAS

• can lead to mid-high VARIABILITY

METHOD: conducting a simple random sample (SRS)

1. label the individuals by assigning them numbers from 1-X

   1. or, write names on slips of paper

2. using an RNG, randomize the labels by choosing [sample size] UNIQUE numbers

   1. or, shuffle slips in a hat and select [sample size] - without repeating any names

3. select the individuals (and conduct the study/administer a survey/etc) that correspond to those numbers

   1. or, select the individuals whose names were chosen

population

entire group/pool of potential people who could be selected for a study

CAN generalize to the population when: random sample FROM that exact population is chosen

convenience sample

sampling method where the experimenter chooses the experimental units that are closest by, the first ones, easiest to reach, etc.

• HIGH BIAS (first ones often have a trait that the rest of the population might not)

voluntary response sample/bias

sampling method where the experimental units/subjects choose to be a part of the sample

• HIGH BIAS: people who choose often have polarized opinions

μ (population mean)

population mean; true value that the sample mean (σ) should be close to

stratified random sample

sampling method where the population is split into homogeneous groups (strata), and SRS’s of the appropriate/representative number are taken from each stratum to make up the whole sample

• LOW BIAS

• LOW VARIABILITY: due to homogeneous groups, groups that tend to be similar in the measured value aren’t going to be disproportionately overrepresented, leading to a lower variability in the calculated sample value

METHOD: conducting a stratified random sample

1. split the population into [#] strata according to [trait]

2. starting with the [X] stratum, assign all [# participants] numbers from 1-X

3. use an RNG to randomly select [stratum sample size] unique numbers between [#-# in the stratum]

   1. with [stratum sample size] being the proper number of experimental units from that stratum, such that the stratum’s representation in the sample is weighted as desired

4. select (and conduct the study upon) the individuals whose labels correspond to the selected numbers

5. repeat this process for the other strata

• added from SRS: splitting population & starting from x stratum; repeating process for other strata

REASONING: conducting a stratified random sample

to reduce variability from an SRS; the strata should be homogeneous in terms of their values that the study is measuring, so limiting how many experimental units come from that stratum will make it imposible to overrepresent values like theirs → less extremity in both directions

cluster sample

sampling method where the population is split into heterogeneous groups (clusters), and then the proper number of those clusters is chosen to create the whole sample

• LOW BIAS

• same VARIABILITY as SRS

• EASIER/LESS COSTLY TO CARRY OUT

METHOD: conducting a cluster sample

1. split the population of [# experimental units] into [#] clusters according to the [cluster reason/group]

2. label each cluster with a number from 1-[# of clusters]

3. using an RNG, choose [# of clusters to select according to sample size; pick ENOUGH clusters to SATISFY sample size] unique numbers from 1-[# of clusters]

4. select the clusters that correspond to the chosen numbers, then select all of the [experimental units] within those chosen clusters

   1. i.e. conduct a census of the cluster

• added from SRS: split population into clusters, label CLUSTERS and CHOOSE # of clusters, then select all individuals within those clusters

systematic random sample

sampling method where a starting individual is randomly identified in the population, and then the individual x individuals away from that individual (x being the interval size) is selected; repeats until the desired sample size is achieved (and should go through the whole population at least once)

METHOD: conducting a systematic random sample

1. label all [experimental units] with a number between 1-X

2. using an RNG, generate a number between 1-[# of the interval’. the [individual] corresponding to this number represents the starting [individual].

3. select the starting [individual]. then, select every [#interval]th player that is past this player on the list, UNTIL [#sample size] players are selected.

• interval selection: if you need sample size of n and population is N, interval should be N/n ish so you go through about the whole population

REASONING: conducting a cluster sample

easy, fast, and cost-effective to collect data from a cluster, because they’re all centralized in the same location(s)

REASONING: conducting a systematic random sample

easy and simpler to carry out and conduct (in some ways)

• if the list is in order of something, it has an effect that reduces variability (assuming the order is homogeneous somehow)

• otherwise, it is just another method of getting a sample

“pathway” to a study

1. population

2. sample frame

   1. undercoverage bias starts here

3. target sample

   1. nonresponse bias starts here (between this & respondents)

4. respondents

   1. response bias starts here

   2. question wording bias starts here

sample frame

the list (in reality) of experimental units available from which a sample is chosen; aimed to be as equal to the population as possible

target sample

selecting a sample from the sample frame using an unbiased method, potentially reducing variability by choosing stratification, etc.

undercoverage bias

when the sample frame is NOT representative of the population; usually, it excludes or favors certain groups in the population

nonresponse bias

when a proportion of the target sample does NOT respond and does NOT become part of respondents

• cause: people can’t be reached or refuse to answer

• effect: less responses, may exclude a certain group (that’s more likely to not answer) from the final respondents group

response bias

when the data gathered from respondents (whether the data itself, the process of getting the data, etc) has bias or issues of some kind and affects the accuracy of the responses

• examples: experimenter’s attire when collecting the data pressures people to give a certain answer so they don’t disappoint the experimenter; people lie to represent themselves in a better light to the experimenter

question wording bias (response bias)

specific type of response bias, where the respondents give inaccurate responses because the question is worded in a manner that pressures them to give a certain response

observational study

study where NO treatments are imposed on experimental units; the subjects are NOT made to do anything

prospective (observational) study

“looking forward” — a type of observational study, where experimental units are identified in advance (potentially collecting data at the beginning), and then later experimenters follow up with the experimental units (no imposition of treatments)

retrospective (observational) study

“looking backward” — a type of observational study, where experimental units are identified and their pasts are inquired about (no imposition of treatments)

experiment

a type of study where treatments are imposed on experimental units

experimental units

participants in the study (can be objects, animals, people, etc); what or who treatments are imposed on

• subjects if the experimental units are human beings

treatments

what is done/not done to experiment units/what is imposed or not imposed; usually the explanatory variable’s options; can include levels OR combinations of the explanatory variables

explanatory variable (factor)

impacts the response variable; the options/treatments possible — must specify:

• “whether or not” if it’s a YES/NO

• the “level” of the treatment if it’s a varying intensity

response variable

the measured variable that is analyzed after the explanatory variable is manipulated

confounding variables

other potential factors that affect or create the results that we observe (especially common in observational studies); related to/influences the explanatory variable (one goes up, other goes down; both go up; both go down), and ALSO influences the response variable (one goes up, other goes down; both go up; both go down)

• MUST SPECIFY relationship/direction between:

  • confounding variable & explanatory variable

  • confounding variable & response variable

• creates illusion that explanatory variable affects the response variable in the way that the confounding variable does

• correlation, but NOT causation

well-designed experiments include…

1. replication

2. random assignment

3. comparison

4. control

replication

repeating the study multiple times, either through multiple trials on the same people OR multiple trials with different groups of people

• increases validity

random assignment

when experimental units are randomly assigned their treatments; reduces bias and potential confounding variables that would result from subjects choosing their own treatments

• benefit: allows us to claim/prove causation between the treatments/explanatory variables & the response variables

• allows GROUPS to be ROUGHLY EQUIVALENT

comparison

having another group, whether a control or an experimental group, to compare results to

• control group: group without treatment that acts as comparison

• experimental group: group receiving a different treatment that acts as comparison

  • required to have an experimental group with another treatment draw conclusions between these 2 different treatments

control

keeping other variables (that may affect results) constant, to reduce potential confounding variables

CONDUCTING: random assignment

1. label all individuals within the sample 1-X

2. using an RNG, select [amount for one treatment] unique #s between 1-X

3. the individuals who were selected receive the [X] treatment

4. if more than 2 treatments: remove the numbers selected and then reselect [amount for one treatment] more unique #s between 1-X that weren’t chosen before; the individuals corresponding to these numbers will receive the [X] treatment…

   1. repeat for all treatments (except the last one:)

5. last treatment: the remaining individuals will receive the [X, last] treatment

placebo effect

when people receive a treatment without an active ingredient/any true effect, they still show “improvement”/get better due to a psychological bias and idea that they should feel better from the treatment

blinding

when the experimenters or the subjects (or both; see double-blinding) are not aware of whether subjects received a real treatment or a placebo

reduces bias:

• for subjects: will not have biased results depending on if they know they got a real treatment or not; can determine if there is the placebo effect

• for experimenters: will not act biased when interacting with subjects depending on their treatment or placebo assignment (e.g. won’t tailor themselves in certain ways, won’t subconsciously hint at/reveal the truth of the treatment)

double-blinding

when NEITHER the experimenters NOR the subjects are aware of whether subjects were given a real treatment or a placebo; reduces bias on both ends (see blinding)

completely randomized design

an experimental design that consists of a single experiment, with experimental subjects in a randomized and heterogeneous sample

block

group of experimental units that are similar with respect to their response (to the measured, response variable)

randomized block design

an experimental design that separates the sample into homogeneous (with respect to their response to the response variable) blocks, then randomly assigns all treatments within each block (as if conducting microcosm-experiments in each block)

• reduces variability** IF blocks are correctly split into homogeneous groups, since their responses are similar to each other

• controls for BLOCKS as confounding variables

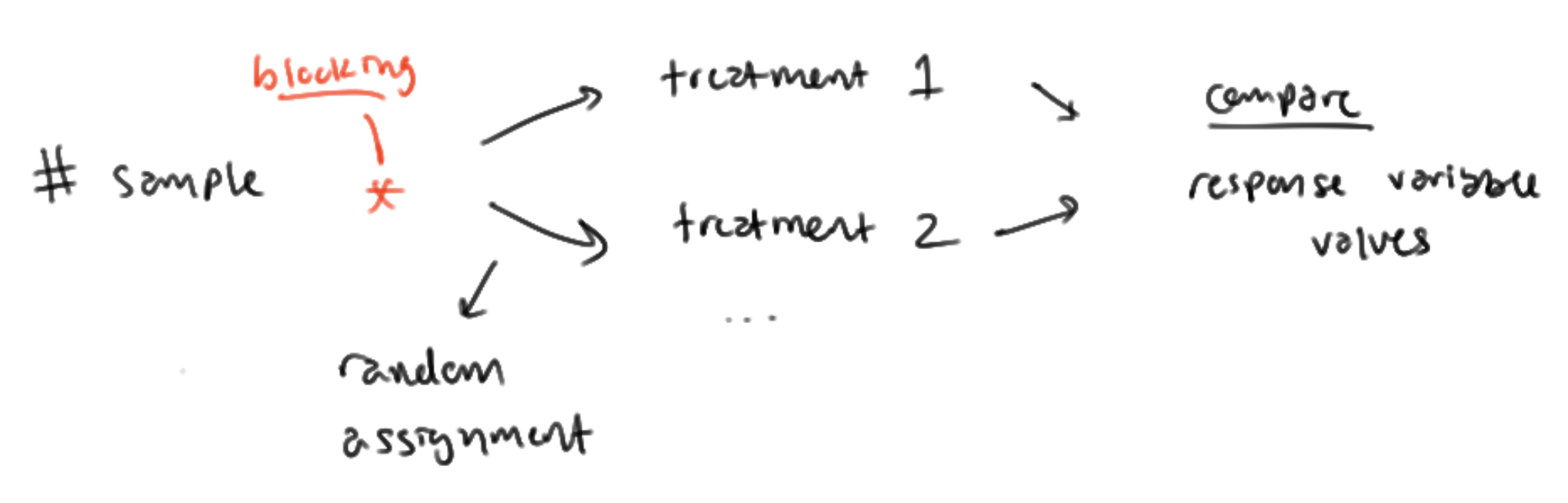
METHOD: conducting a randomized block design (writing)

1. separate the [experimental units] into blocks of [X] (specify all blocks). within each block, number the [experimental units] from 1-X

2. for the first block, use an RNG to select [X] unique numbers, and give the individuals who correspond to those numbers the [X] treatment. (specify the other treatments…) repeat this step for every block

3. compare their [response variable/effect] in each of the blocks

4. finally, bring all the blocks together to combine and compare overall

METHOD: randomized block design with ONE factor (diagram)

METHOD: randomized block design with MULTIPLE factors (diagram)

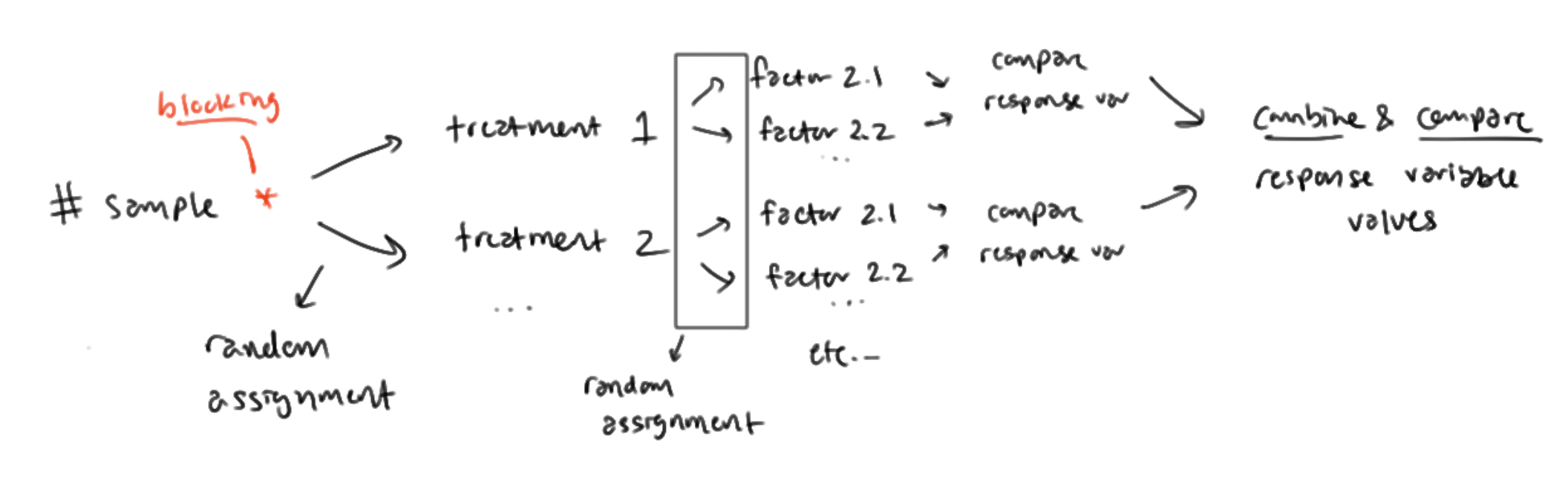
REASONING: randomized block design

Randomized block design helps to:

1. control for ____ (what the blocks are sorted for) as a confounding factor.

Within each block, there will be:

2. lower variability of results

making it easier to determine ____ (what the experiment is trying to determine)

REASONING: confounding variables are problems

If [an effect is observed], we wouldn’t know if it was because of [explanatory variable] or because of [confounding variable], as [confounding variable] may be a confounding variable and we would not correctly determine causality.

matched pairs design

a type of randomized block design where the “blocks” are pairs, of either 2 very similar subjects OR 1 person but 2 trials/2 parts of the subject

• 2 subjects: the two subjects are randomly assigned to 1 of 2 treatments, and results are compared

• 1 subject: each subject receives 2 treatments, still randomized: e.g. the order in which they receive them is randomized; where they receive them (e.g. on two comparable parts of their body, like right/left leg) is randomized; results are compared

METHOD: conducting a matched pairs design

1. if 2 subjects: pair 2 very similar/comparable subjects, then the next two, and so on, forming [#] pairs. label the first person in the pair “1,” and the second “2”

   1. randomize: using an RNG, select 1 or 2. for the first pair, the subject corresponding to the # selected will receive [X] treatment; the other subject will receive [Y] treatment

2. if one subject: for each subject, run the RNG for 1 or 2, and then assign [X] treatment first/on the right/etc if 1, second/on the left if 2 (or something similar)

3. repeat the above for all pairs/subjects

4. compare the difference between the two treatments for every pair of subjects/subject

simulation

used to determine the chance of an event, statistic value/threshold, etc. of occurring by chance alone; repeatedly randomly assigns the values to random labels and plots results on a scatterplot

confidence interval %

the chance that, if explanatory does NOT affect response variable, you obtain the result that you got by chance alone

• found by repeatedly simulating the data points by randomly assigning them to the results & creating a scatterplot of how many got a certain % of results

CALCULATION: confidence interval %

confidence interval % for your result = [# of points ≥ yours]/[total # points] * 100%

statistically significant (CI 5%)

when the results of an experiment are unlikely (less than 5%, >=5%) to happen by chance alone

• if it IS statistically significant, we have convincing evidence that the treatment caused a difference

scope of inference

whether we can conclude causality, and to what extent we can infer the results and generalize to what population

when can we conclude causation?

when random assignment of treatments is present

when can we conclude generalization to the population?

when a random sample from THAT POPULATION is taken

• can be inferred up to the population that the sample was taken from (i.e. up until the point that all those that could have been chosen)