Cálculo III (vectorial)

Parametrización de una circunferencia con centro (h,k) y radio r

x = r cos(θ) + h, y = r sin(θ) + k. Es una forma de recorrer la circunferencia usando el ángulo θ como parámetro.

Parametrización de la cicloide

x = rθ − r sin(θ), y = r − r cos(θ). Representa la trayectoria de un punto sobre la circunferencia que rueda sin resbalar sobre una línea recta. Es una curva periódica.

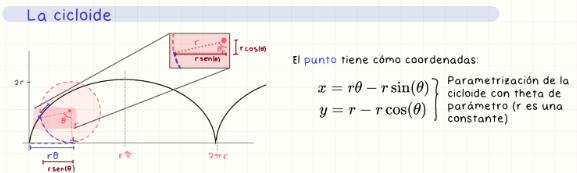
Coordenadas polares

Sistema de coordenadas que representa un punto por su distancia al origen (r) y el ángulo θ respecto al eje x. La relación con coordenadas cartesianas es: x = r cos(θ), y = r sin(θ)

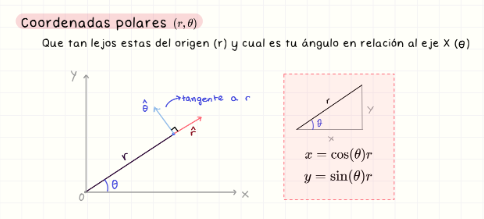
Si r es constante

Describe un círculo de radio fijo, ya que el punto está a una distancia fija del origen.

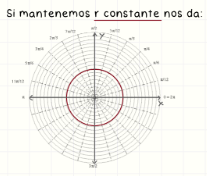
Si θ es constante

Describe una línea recta que pasa por el origen en dirección fija.

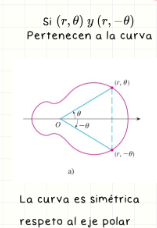
Simetría respecto al eje polar

La curva es simétrica si (r, θ) y (r, −θ) pertenecen a ella. Ejemplo: cos(−θ) = cos(θ). Es una reflexión respecto al eje x.

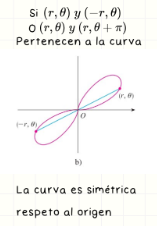
Simetría respecto al origen

La curva es simétrica si (r, θ) y (−r, θ + π) o (r, θ) y (r, θ + π) están en la curva. Implica una rotación de 180° respecto al origen.

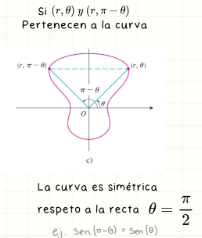
Simetría respecto a θ = π/2

La curva es simétrica si (r, θ) y (r, π − θ) pertenecen a la curva. Es una reflexión respecto al eje y.

Límite de una función vectorial

El límite de r(t) cuando t → a es el vector formado por los límites de sus componentes. Es necesario que todos existan para que el límite exista.

Continuidad de una función vectorial

Una función vectorial es continua en t = a si el límite de r(t) al acercarse a a es igual al valor r(a). Equivale a la continuidad de cada componente.

Derivada de una curva paramétrica (dy/dx)

Si x = x(t), y = y(t), entonces dy/dx = (dy/dt) / (dx/dt). Esta razón representa la pendiente de la recta tangente a la curva.

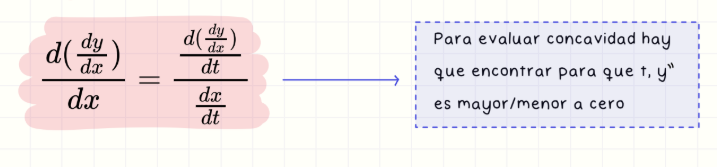
Segunda derivada paramétrica considerando r(t) (d²y/dx²)

La segunda derivada d²y/dx² se calcula como: (d/dt (dy/dx)) / (dx/dt). Se usa para determinar la concavidad de la curva.

Significado de r'(t)

Es el vector tangente a la curva. Representa la dirección y velocidad con la que una partícula se mueve sobre la curva.

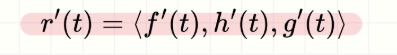
Norma de r'(t)

Se interpreta como rapidez o magnitud de la velocidad. Es un número positivo que indica qué tan rápido se recorre la curva sin importar la dirección.

TFC: ∫_b ^a r'(t) dt

∫ r'(t) dt = r(b) − r(a). Representa el desplazamiento neto entre dos puntos en la curva.

Longitud de una curva

Se calcula con ∫ ||r'(t)|| dt. Suma la magnitud de los pequeños desplazamientos para obtener la longitud total recorrida sobre la curva.

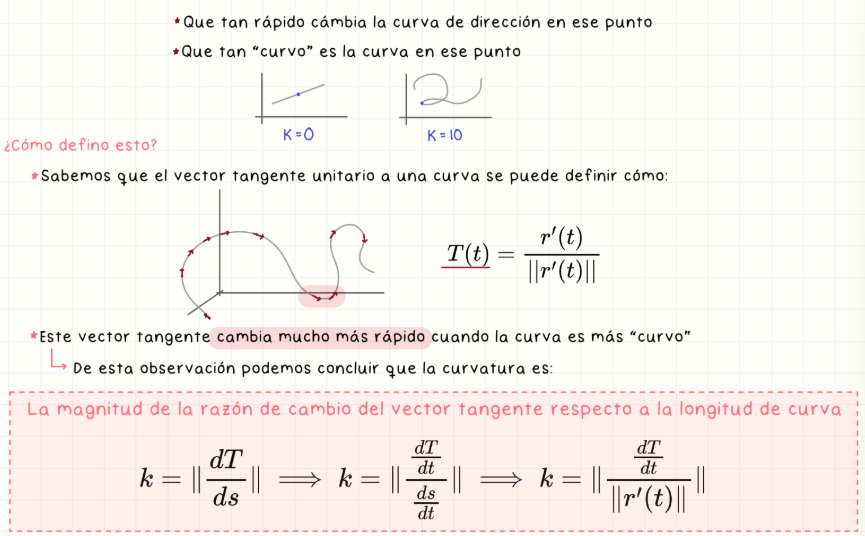
Curvatura (definición con T)

La curvatura k es la razón de cambio del vector tangente unitario respecto a la longitud de arco: k = ||dT/ds|| = ||dT/dt|| / ||r'(t)||. Indica qué tan rápido cambia la dirección.

Curvatura (definición alternativa solo con r(t))

Fórmula útil cuando conocemos r'(t) y r''(t), especialmente en coordenadas cartesianas.

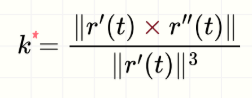
Vector tangente unitario

T(t) = r'(t)/||r'(t)||. Representa la dirección del movimiento sobre la curva. Siempre apunta en la dirección de avance.

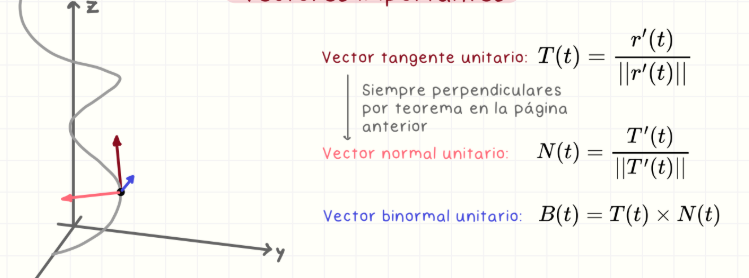
Vector normal unitario

N(t) = T'(t)/||T'(t)||. Indica hacia dónde gira la curva, es perpendicular al vector tangente.

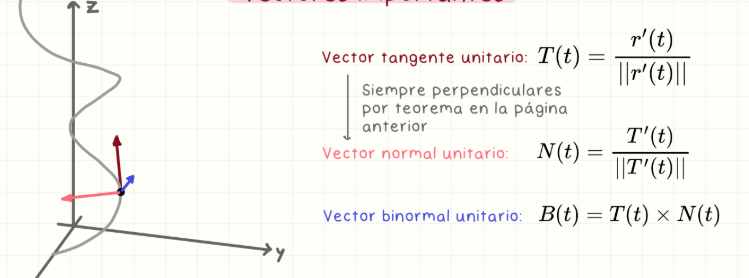
Vector binormal unitario

B(t) = T(t) × N(t). Perpendicular tanto a T como a N. Forma una base ortonormal en el espacio tridimensional.

Plano osculador

Plano determinado por T y N en un punto. Es el plano que mejor se ajusta a la curva en ese punto, como si “rozara” la curva.

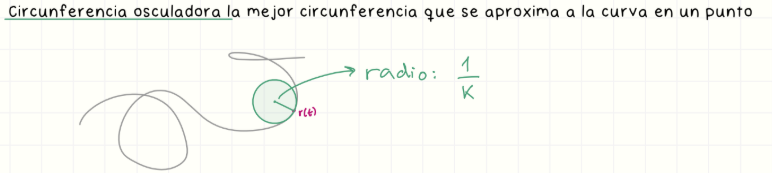
Circunferencia osculadora

Es la circunferencia que mejor se aproxima a la curva en un punto. Su radio es 1/k, donde k es la curvatura.

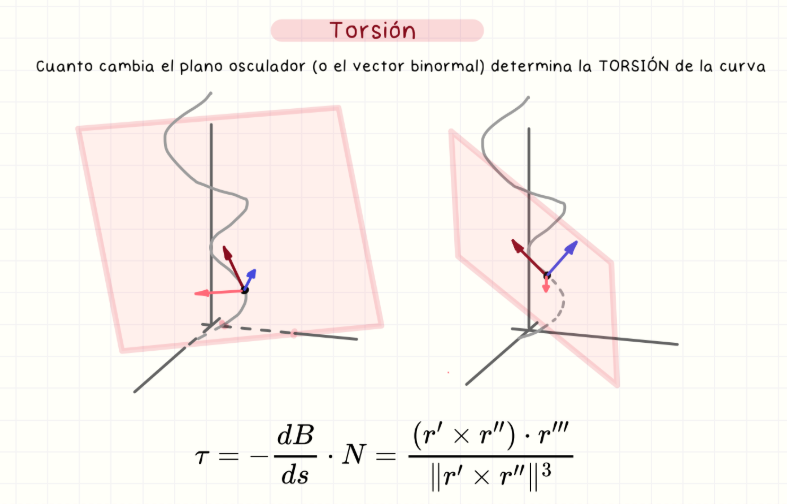
Torsión

Mide cuánto cambia el plano osculador a lo largo de la curva. Se define como τ = −dB/ds · N, o usando triple derivada y producto cruzado.

Fórmulas de Frenet-Serret

Relaciones entre derivadas de T, N y B respecto al arco:
dT/ds = kN
dN/ds = −kT + τB
dB/ds = −τN

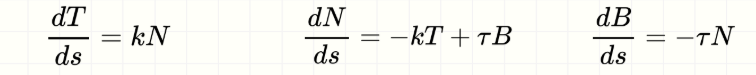
Campo escalar

Función que asigna un número real a cada punto del espacio: f: ℝⁿ → ℝ. Ejemplo: temperatura en un punto del espacio.

Campo vectorial

Función que asigna un vector a cada punto: F: ℝⁿ → ℝⁿ. Cada componente puede depender de múltiples variables.

Campo gradiente

Dado un campo escalar f, su gradiente ∇f es un campo vectorial. Apunta en la dirección de máximo crecimiento de f.

Campo conservativo

Un campo vectorial F es conservativo si existe un escalar f tal que ∇f = F. Solo se puede definir en regiones simplemente conexas.

Función potencial

Función escalar f tal que ∇f = F. Se interpreta como la energía potencial asociada al campo vectorial.

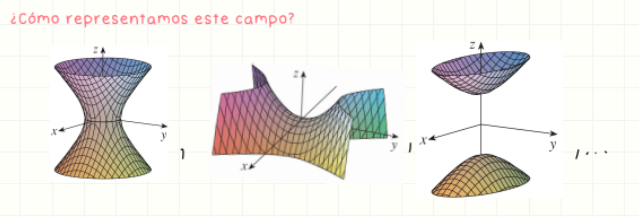
Integral de línea sobre una función escalar

Representa el área "bajo" la curva sobre la superficie z = f(x,y).

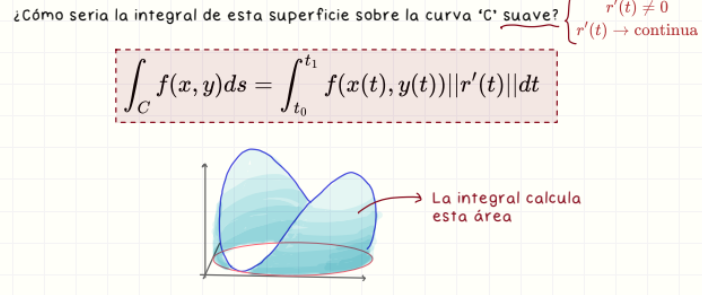
Integral de línea respecto a x e y

∫ f(x,y) dx = ∫ f(x(t), y(t)) x'(t) dt.
∫ f(x,y) dy = ∫ f(x(t), y(t)) y'(t) dt.
Dependen de la orientación de la curva.

Integral de línea sobre campo vectorial

∫ F·dr = ∫ P dx + Q dy. Representa el trabajo hecho por el campo al recorrer una curva.

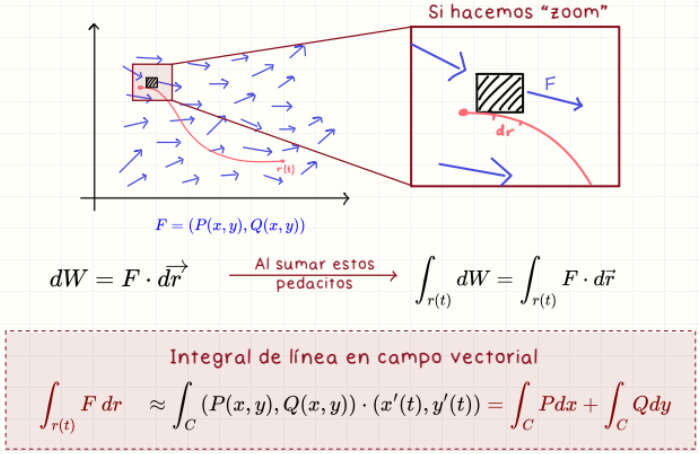
Otras formas de integral de linea sobre campo vectorial

Teorema fundamental del cálculo en campos

Si F es conservativo y F = ∇f, entonces ∫_C F·dr = f(r(t₁)) − f(r(t₀)). La integral solo depende del punto inicial y final.

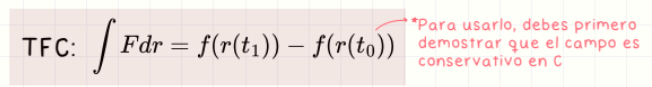
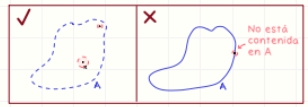
Conjunto abierto

Un conjunto es abierto si para cualquier punto dentro de él, puedes moverlo ligeramente en cualquier dirección y seguir dentro del conjunto.

Conjunto cerrado

Un conjunto es cerrado si contiene todos sus puntos límite. Ejemplo: incluye su borde.

Conjunto disconexo

Existe una separación entre sus partes. Se puede dividir en dos conjuntos abiertos no vacíos, disjuntos, cuya unión es el conjunto original.

Conjunto conexo

No es disconexo. Hay un "camino" continuo dentro del conjunto entre cualquier par de puntos.

Conjunto simplemente conexo

Es conexo y no tiene agujeros. Toda curva cerrada dentro del conjunto se puede contraer a un punto sin salir del conjunto.

Curva cerrada

Curva en la que el punto inicial coincide con el final. Si el campo es conservativo, la integral de línea sobre una curva cerrada es cero.

Curva con orientación positiva

Una curva cerrada tiene orientación positiva si, al recorrerla, la región que encierra (como un lago) queda siempre a la izquierda. Es la orientación habitual para aplicar teoremas como el de Green.

Curva suave a trozos

Una curva se considera suave a trozos si puede dividirse en un número finito de segmentos en los cuales cada uno tiene derivada continua, y las uniones entre ellos son continuas. Puede haber quiebres, pero sin saltos.

Teorema de equivalencia para curvas en campos conservativos

Para un campo vectorial continuo en un dominio conexo y una curva suave a trozos, se cumple que las siguentes afirmaciones son equivalentes:

1. F es conservativo.

2. La integral de línea es independiente del camino.

3. La integral sobre cualquier curva cerrada contenida en el dominio es cero.

Teorema de Green

Relaciona una integral de línea sobre una curva cerrada con una doble integral sobre la región que encierra:
∮_C P dx + Q dy = ∬D (∂Q/∂x − ∂P/∂y) dA.
Se requiere que la curva sea simple, cerrada, suave por tramos y con orientación positiva.

Condición de campo conservativo en 2D

Si ∂Q/∂x = ∂P/∂y entonces el campo F = (P, Q) es conservativo, siempre que la región sea simplemente conexa.

Gradiente

El operador gradiente ∇ mide el cambio más rápido de un campo escalar en el espacio. Representa la dirección de mayor incremento y se define como:
∇ = (∂/∂x, ∂/∂y, ∂/∂z).

Divergencia

Mide cuánto "flujo" sale de un punto. Si Div(F) > 0 hay más salida que entrada de flujo. Se define como:
Div(F) = ∇ · F = ∂P/∂x + ∂Q/∂y + ∂R/∂z.

Campo incompresible

Un campo es incompresible si Div(F) = 0, es decir, no hay ganancia ni pérdida de volumen en el flujo.

Rotacional

Mide la tendencia de un campo vectorial a rotar alrededor de un punto. Se define como:
rot(F) = ∇ × F.
Si es cero, el campo no tiene rotación local.

Condición para ser conservativo

Un campo vectorial F es conservativo si y solo si su rotacional es cero en una región simplemente conexa.

Teoremas de identidades vectoriales (div-rot-grad)

div(rot(F)) = 0.
rot(grad(f)) = 0.
Estas son propiedades algebraicas de los operadores vectoriales.

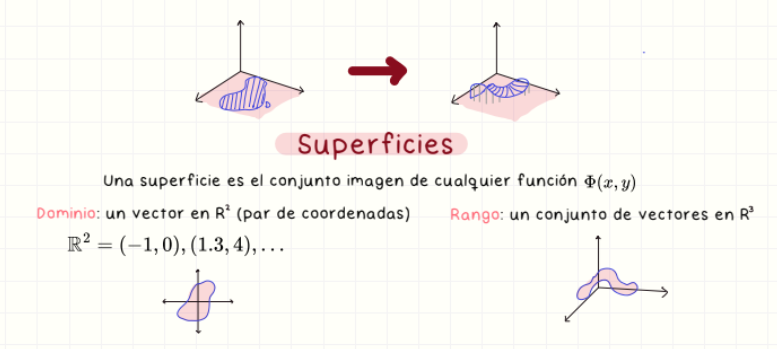
Superficies

Una superficie es el conjunto imagen de una función vectorial de dos variables Φ(u,v). Está definida sobre un dominio en ℝ² y toma valores en ℝ³.

Coordenadas cilíndricas

Extienden las polares añadiendo una coordenada z.
Φ(θ,z) = (a + r cos(θ), b + r sin(θ), z).
D: [0, 2π] × ℝ.

Coordenadas esféricas

Representan puntos en términos de su radio y dos ángulos.
Φ(θ, φ) = (a + r cos(θ) sin(φ), b + r sin(θ) sin(φ), c + r cos(φ)).
D: [0, 2π] × [0, π].

Superficies de revolución forma y = f(x)

Superficies de revolución forma y(t) = (a(t), b(t)

Punto regular

Un punto (u₀, v₀) de una superficie es regular si los vectores ∂Φ/∂u y ∂Φ/∂v no son colineales, es decir, su producto cruz no es cero.

Superficie regular

Es aquella cuya parametrización hace que todos sus puntos sean regulares. Admite normal bien definida en cada punto.

Superficie suave

Una superficie regular cuya parametrización es de clase C¹, es decir, sus derivadas son continuas.

Vector normal

En un punto regular, el vector normal a la superficie es:
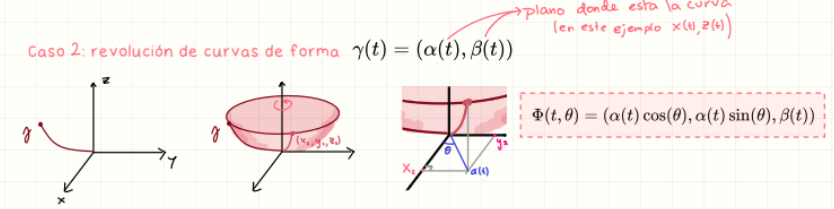
n = ∂Φ/∂u × ∂Φ/∂v.

Vector normal unitario

Se obtiene normalizando el vector normal:
n̂ = (∂Φ/∂u × ∂Φ/∂v) / ||∂Φ/∂u × ∂Φ/∂v||.

Campo normal

Es una función que asigna un vector normal a cada punto de una superficie. Si es continuo, la superficie es orientable.

Plano tangente a superfice

En un punto Φ(u₀, v₀), el plano tangente tiene ecuación:
n · (X − X₀) = 0, donde n es el vector normal en ese punto.

Área de una superficie

Se calcula mediante la norma del producto cruz entre los vectores tangentes a las curvas coordenadas:
Área = ∬ ||∂Φ/∂u × ∂Φ/∂v|| dA.

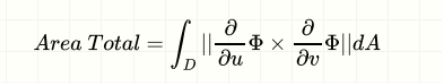
Integral de superficie de campo escalar

Representa el “volumen” bajo la superficie si f ≥ 0. Se define como:
∬ f dS = ∬ f(Φ(u,v)) ||∂Φ/∂u × ∂Φ/∂v|| du dv.

Centro de masa de una lámina

Si ρ(x,y,z) es la densidad superficial, el centro de masa se calcula como:
(x̄, ȳ, z̄) = (1/m) ∬ xρ dS, ∬ yρ dS, ∬ zρ dS.

Superficie orientable

Una superficie es orientable si se puede asignar un campo normal continuo. No todas las superficies lo permiten (ej: banda de Möbius).

Orientación natural

Es la orientación que resulta de una parametrización dada. Se define como “hacia arriba” si el vector normal apunta en esa dirección. En superficies cerradas, la orientación natural implica que el campo normal apunta hacia afuera.

Integral de superficie de campo vectorial

Representa el flujo del campo a través de una superficie. Se expresa como:
∬ F · dS = ∬ F(Φ(u,v)) · (∂Φ/∂u × ∂Φ/∂v) du dv.
Mide cuánto atraviesa el campo la superficie por unidad de tiempo.

Independencia de la parametrización en Integral de superficie de campo vectorial

La integral de superficie no depende de cómo esté parametrizada, siempre que se conserve la orientación. Si se invierte la orientación, la integral cambia de signo.

Aplicación: Ley de Gauss

El flujo eléctrico de un campo E a través de una superficie S se relaciona con la carga encerrada por:
Q = ε₀ ∬ E · dS
Es uno de los pilares del electromagnetismo.

Teorema de Stokes

Relaciona la circulación de un campo sobre una curva cerrada con el flujo de su rotacional a través de una superficie que tiene esa curva como borde:
∮ F · dr = ∬ rot(F) · dS.
La orientación del borde y de la superficie debe seguir la regla de la mano derecha.

Stokes con dos curvas de borde

Si una superficie tiene dos curvas de borde, se puede cerrar una de ellas artificialmente y aplicar Stokes considerando las orientaciones. El resultado es la suma de ambas integrales de línea.

Teorema de la divergencia (Gauss)

Relaciona el flujo de un campo vectorial F a través de la superficie frontera de una región sólida E.
Mide el “flujo neto” que entra o sale del volumen.

Volumen de una región E en ℝ³

∭ div F dV representa el volumen si div F = 1