(digital) math sat practice (copy)

formula/content *must know* for the math portion of the dsat; content sourced from: Scalar Learning (YT), Epic Prep (YT), LearnSATMath (YT), Google, The College Panda (textbook), & ChatGPT..

point-slope form

y - y1 = m(x - x1)

*use when given slope and a coordinate

same slope, different y’s

parallel lines

circle formula

(x - h)² + (y - k)² = r²

(h, k) = center of the circle

slope of a line when given coordinates

m = y₂ - y₁ / x₂ - x₁

slope intercept form

y = mx + b

m = slope → rise/run

b = y-intercept

midpoint formula

(x₁ + x₂ / 2 , y₁ + y₂ / 2)

*midpoint = average of two points

distance formula purpose

to find radius of circle, given center point/one exterior; to find hypotenuse w/o pythagorean theorem

distance formula

d = √(x₂ - x₁)² + (y₂ - y₁)²

length of an arc formula

L = (n/360)2πr

n = angle made by r; L = crust of the pizza slice

area of a sector

A = (n/360)πr²

A = area of the slice of pizza

quadratic formula

x = 1/2(a) (-b ± √b²-4(a)(c))

when quadratic equation = 0, x values are the solution

quadratic standard form

y = ax² + bx + c

when quadratic equation = 0, x values are the solution

soh cah toa

sine = opposite/hypotenuse

cosecant = hypotenuse/opposite

cosine = adjacent/hypotenuse

secant = hypotenuse/adjacent

tangent = opposite/adjacent

cotangent = adjacent / opposite

similar triangles (same angles + proportionate side lengths)

sine of corresponding angles are equal

probability

number of favorable outcomes / total number of outcomes

exponential growth

y = a(1 + r)^t

a = initial value; r = growth rate; t = time

exponential decay

y = a(1 - r)^t

a = initial value; r = growth rate; t = time

vertex of a parabola formula when in quadratic standard form

(x, y)

x = -b/2a

y = that x value plugged back into the original equation (that you got the b and a values from)

vertex form

y = a(x - h) + k

vertex: (h, k)

pythagorean theorem

a² + b² = c²

a & b = legs

c = hypotenuse

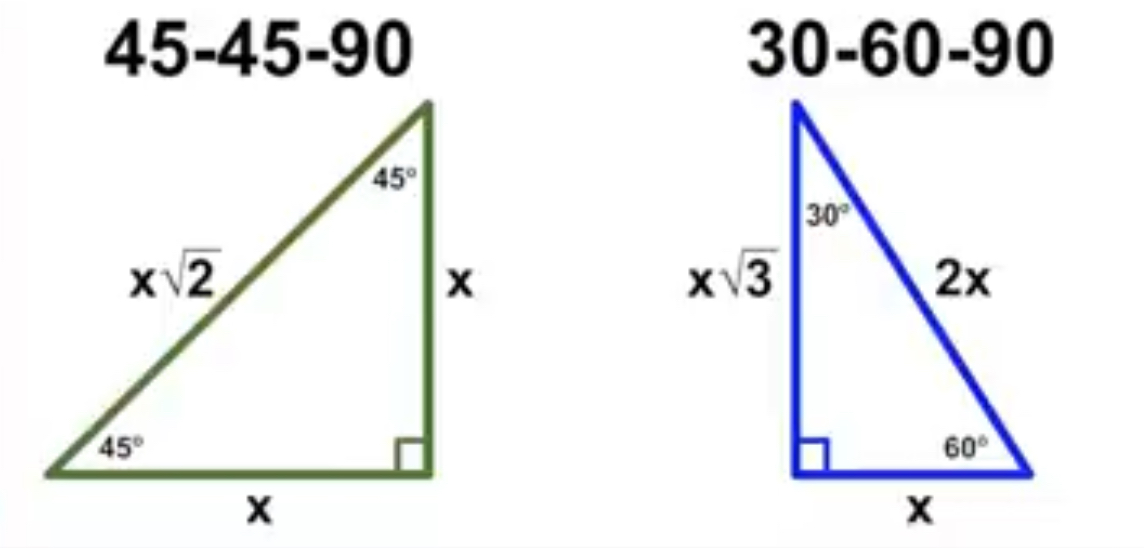
special right triangles

45º-45º-90º → leg 1: x, leg 2: x, hypotenuse: x√2

• hypotenuse ÷ √2 = leg

30º-60º-90º → small leg: x, big leg: x√3, hypotenuse: 2x

• small leg x √3 = big leg

• big leg ÷ √3 = small leg

• small leg x 2 = hypotenuse

distance formula (rate)

d = rt

d = distance; r = rate (rate = speed); t = time

*units of rate must equal units of time

sin/cosine relationship

*sin(x) = cos(90 - x)

x = angle

90 - x = complement of that angle

sin(10) = cos(80)

sin(20) = cos(70)

sin(30) = cos(60)

sin(40) = cos(50)

sin(50) = cos(40)

sin(60) = cos(30)

sin(70) = cos(20)

sin(80) = cos(10)

*equals 90º → definition of complementary angles: two angles that up to 90º

sum of solutions of quadratic

0 = ax² + bx + c

sum of solutions = -b/a

product of solutions of quadratic

0 = ax² + bx + c

product of solutions: c/a

discriminant (of quadratic)

0 = ax² + bx + c

b² - 4(a)(c)

discriminant = stuff under the radical in quadratic formula

find number of solutions (quadratic)

use discriminant to solve

x < 0 (negative; imaginary solutions) → no real solution

x = 0 → one real solution

x > 0 (positive) → two real solutions

area of equilateral triangle

∆ → all sides equal s

area of equilateral triangle = s²√3/4

pythagorean triples

3-4-5

• 6, 8, 10 (× 2)

• 9, 12, 15 (× 3)

• 12, 16, 20 (× 4)

• 15, 20, 25 (× 5)

5-12-13

• 10, 24, 26 (× 2)

• 15, 36, 39 (× 3)

• 20, 48, 52 (× 4)

• 25, 60, 65 (× 5)

7-24-25

• 14, 48, 50 (× 2)

• 21, 72, 75 (× 3)

• 28, 96, 100 (× 4)

• 35, 120, 125 (× 5)

8-15-17

• 16, 30, 34 (× 2)

• 24, 45, 51 (× 3)

• 32, 60, 68 (× 4)

• 40, 75, 85 (× 5)

*multiply all sides by a value to find the sides when you know its a pythagorean triple

perpendicular slope

slope → m = a/b

perpendicular slope (opposite reciprocal of slope) → m = -b/a

parallel slope

slope → m = a/b

parallel slope → m = a/b

*slopes are the same

sum of angles formula (for any polygon)

sum = (n - 2)180º

n = number of sides

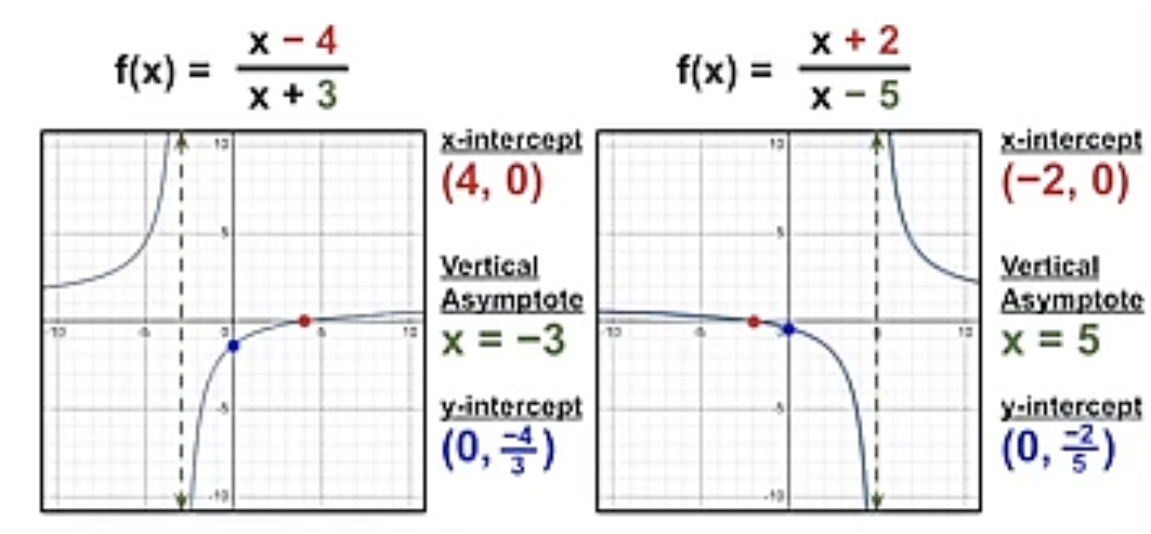
rational functions

x-intercept

• equation: set numerator equal to zero

• graph: where the line touches the x-axis (same as the zeroes)

y-intercept

• equation: plug in 0 for x in the equation

• graph: where the line touches the y-axis

vertical asymptote

• equation: set denominator equal to zero

• graph: find the line the function is approaching but never meeting

horizontal asymptote

• equation: f the degree of the numerator is less than the degree of the denominator, it’s y = 0; if the degree of the numerator is equal to the degree of the denominator, y = leading coefficient/leading coefficient; if the degree of the numerator is greater than the degree of the denominator, there is no horizontal asymptote)

• graph: find the line the function is approaching but never meeting

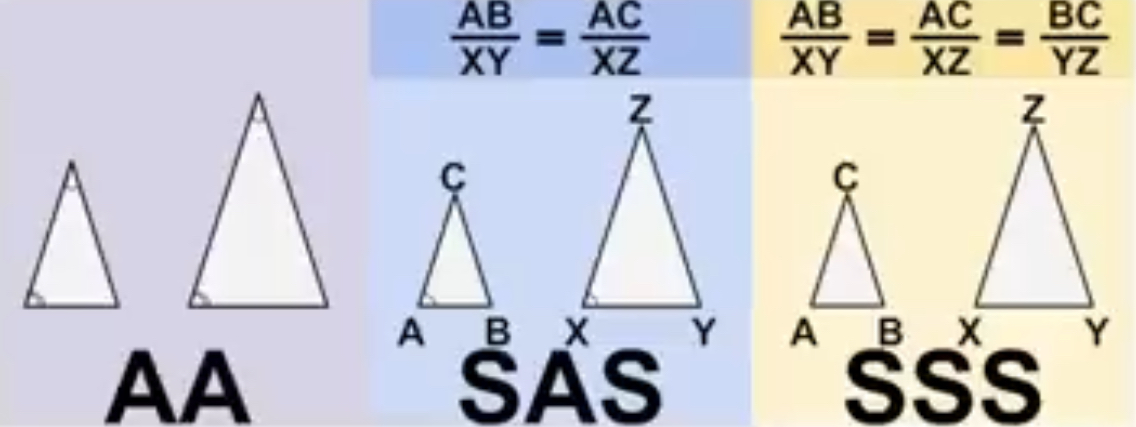
triangle congruence theorems

SSS - side-side-side

SAS - side-angle-side

ASA - angle-side-angle

AAS - angle-angle-side

HL - hypotenuse-leg

*must be in this exact order

triangle similarity theorems

SSS - side-side-side

SAS - side-angle-side (congruent angles, proportionate sides)

AA - angle-angle

*sides proportionate and not congruent; angles are always congruent

unit circle

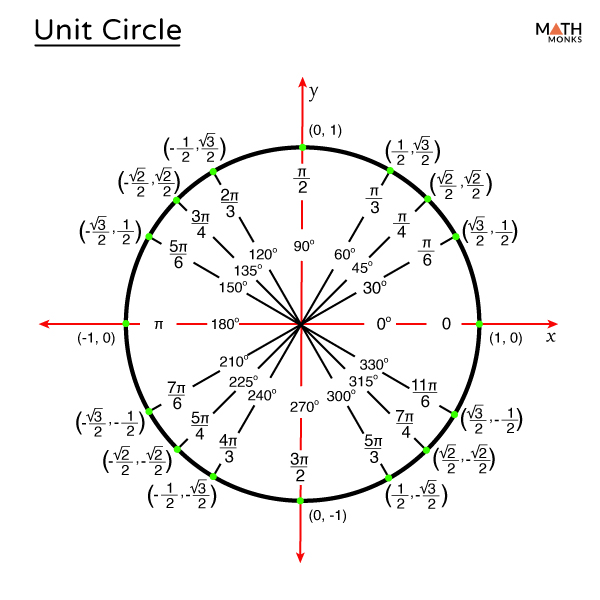
sin(Θ) = y

cos(Θ) = x

tan(Θ) = y/x

exponent rules (7)

x^a • x^b → x^a+b

(x^a)^b → x^a•b

x^a / x^b → x^a-b

x^-a → 1 / x^a

x⁰ → 1

x¹ → x

x^a/b → b√x^a

absolute value

|ax - b| = c

• two equations:

  • ax - b = c

  • ax - b = -c

• solve for x → two solutions

inequalities

-ax - b < c

*-ax < b+c

*when dividing (or multiplying) -a on both sides, you have to switch the sign

answer: x > b+c/a

solutions in systems of equations

no solution = parallel lines (same slope)

infinite solutions = same line (same slope, same y-intercept)

one solution = lines intersect at a single point (different slopes)

inscribed angle theorem

any inscribed angle that extends from the same arc as the center angle will always be ½ of the center angle

inscribed angle theorem of the diameter

if a point lies on the circumference and is connected to the endpoints of the diameter, it forms a right angle with the diameter

simple interest formula

A = p (1 ± r)^t

A = amount; p = principal amount; r = rate; t = time

compound interest formula

A = p (1 ± r/n)^nt

A = amount; p = principal amount; r = rate; n = number of times interest is applied per time period; t = time

integer vs. non-integer

integer: positive/negative whole number (including zero)

non-integer: not a positive/negative whole number/zero; decimal or fraction

use vertex form for quadratic (minimum or maximum)

y = a(x - h)² + k

positive a: parabola opens upwards and k represents the minimum value

negative a: parabola opens downwards and k represents the maximum value.

when there’s one solution between a quadratic and horizontal line

the solution is at the vertex

when to use desmos for no solution problems

quadratic = YES

systems of equations (linear) = NO (just make the slopes equal)

percent change formula

percent change = 100% (new value - original value / original value)

*if the problem is worded as “percent greater/less than,” the quantity that comes after “than” should be taken as the original value

p% of x

p/100 × x

p% greater than x

(1 + p/100)x

p% less than x

(1 - p/100)x

square inscribed in a circle

the diagonal of a square is equal to the diameter of the circle it is incribed in

square relationship between its diagonal and side lengths (formula)

d = s√2

d = diagonal; s = side length

when to use desmos

• finding the vertex

• x/y-intercepts

• quadratics that intersect at 1/0 points

• finding (basic) mean/median

• finding points on a circle

• systems of equations/inequalities

• number of solutions

180º

equals π radians

radians/degrees conversion

radian = degree × 180/π

degree = radian × π/180