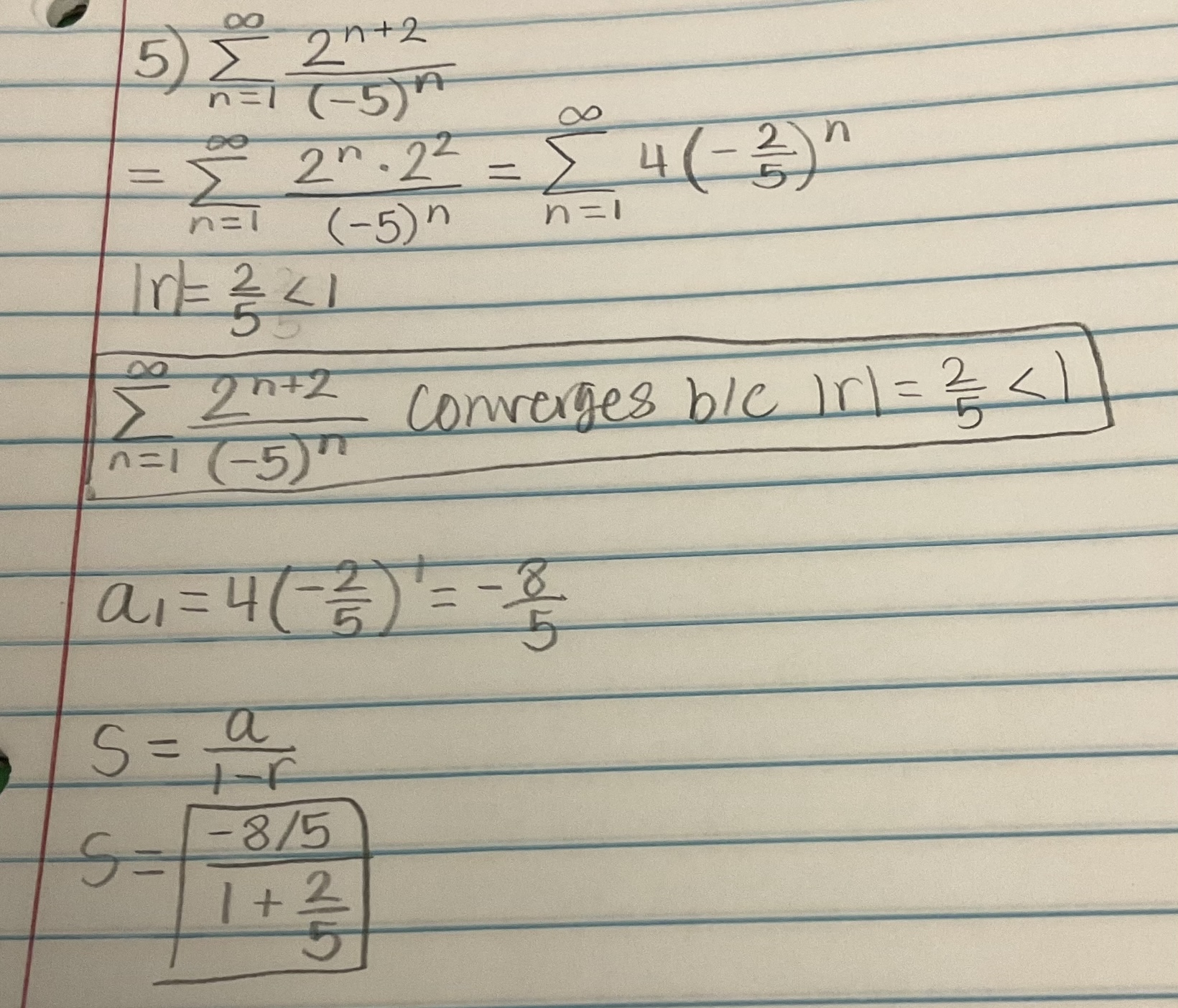MATH 227: 11.2 (Series - Convergent/Divergent)

1. How to determine if a series is geometric

2. How to determine if a geometric series is convergent or divergent

3. If the geometric series is convergent, what formula do you use to find the sum of the series

A. Any time you see n in the exponent of all bases in the function or you see #/base with n exponent

B. Convergent when n < 1 and Divergent when n ≥ 1

C. a / 1 - n

1. How to determine if a series is a telescoping sum

2. How to determine if a telescoping series is convergent or divergent

1. any time you see # / polynomial (where the polynomial can be factored or is already fully factored) or any time you see (# / n) - (# / n)

2. If the limit exits at the end

1. What is the Divergence Test?

2. How can you recognize when to use it and to you use it.

2. • The first way is if the function looks like a sequence where you would just divide the numerator and denominator by the leading coefficient in the denominator to find the limit (in order to do this, divide the numerator and denominator by the leading coefficient in the denominator, simplify it, and find the limit. If the limit is anything but, 0 then its divergent and the Divergence Test works

   • The second way is if a function is in inside another function and there inside function looks like a sequence where you would just divide the numerator and denominator by the leading coefficient in the denominator to find the limit (in order to do this, take the inside function and divide the numerator and denominator by the leading coefficient in the denominator, simplify it, and find the limit. Then plug the value of the limit into the outside function and if the value is anything but, 0 then its divergent and the Divergence Test works

   • If you do the alternating series test and the limit does not equal 0, then use the Divergence Test

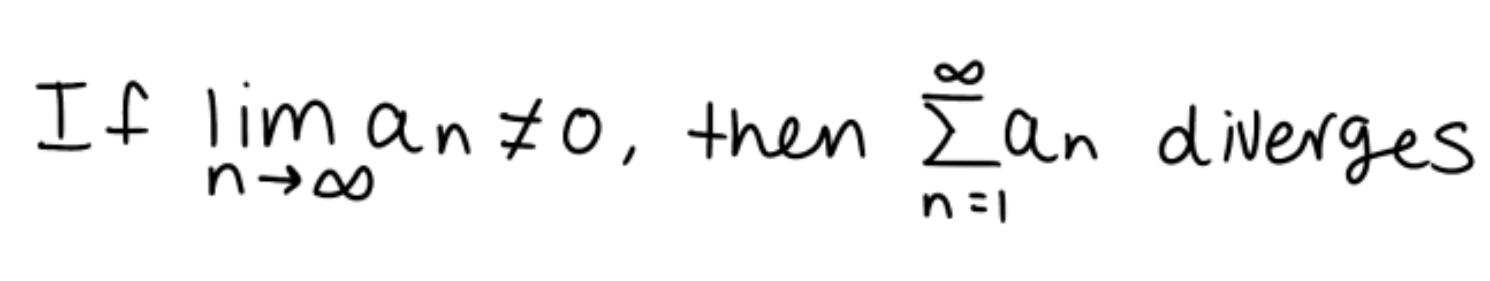
Write the 3 properties of CONVERGENT Series

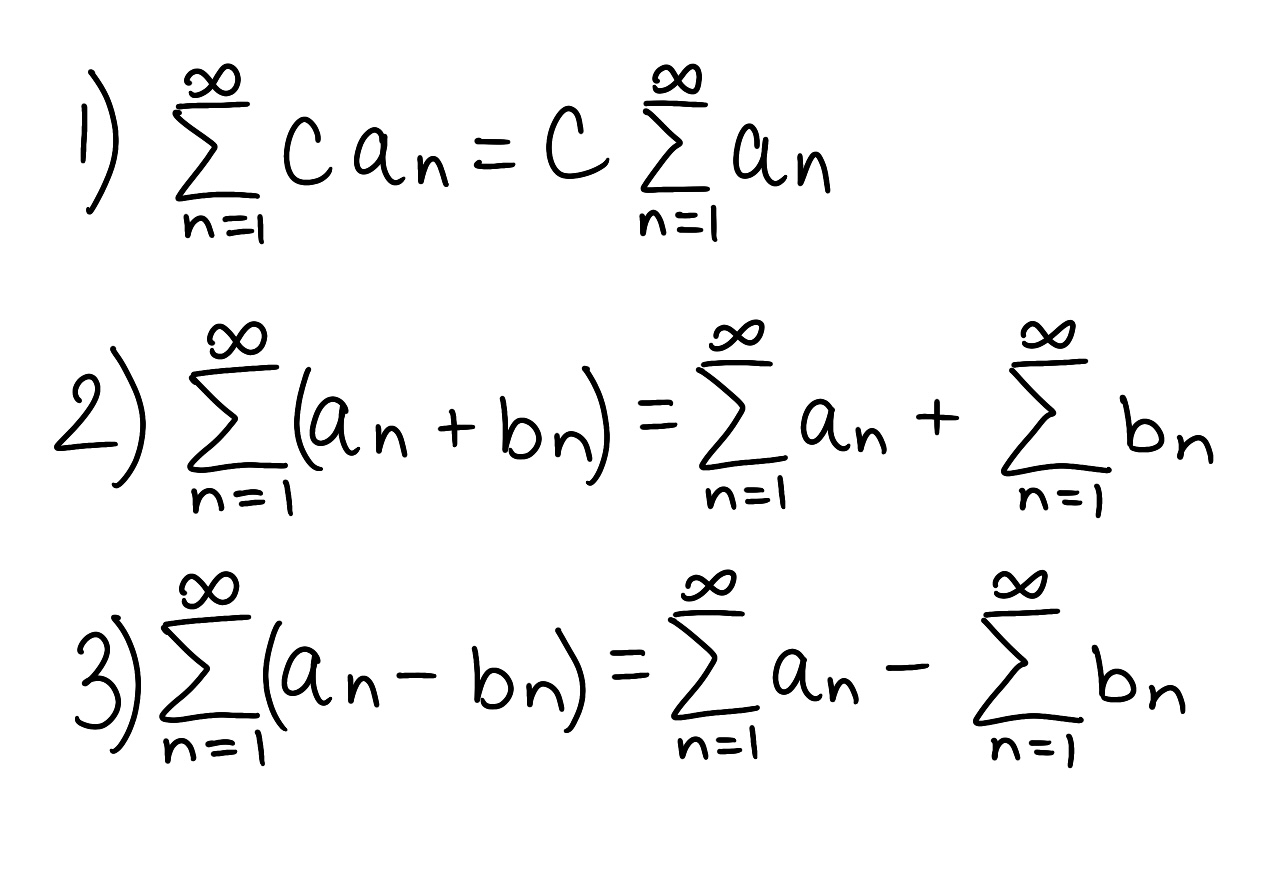
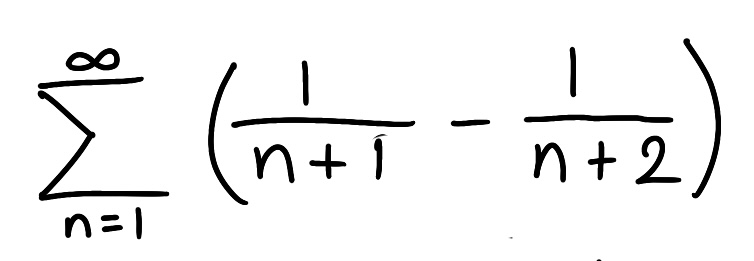
Determine if the series is convergent or divergent. If the series converges, find its sum (if it’s a geometric or telescoping series)

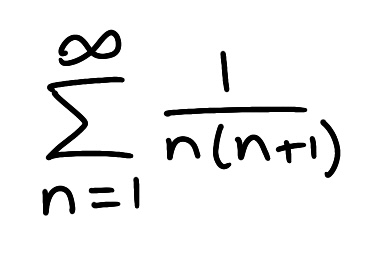
Determine if the series is convergent or divergent. If the series converges, find its sum (if it’s a geometric or telescoping series)

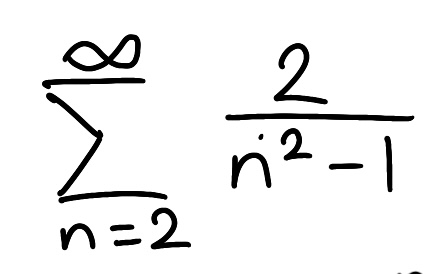
Determine if the series is convergent or divergent. If the series converges, find its sum (if it’s a geometric or telescoping series)

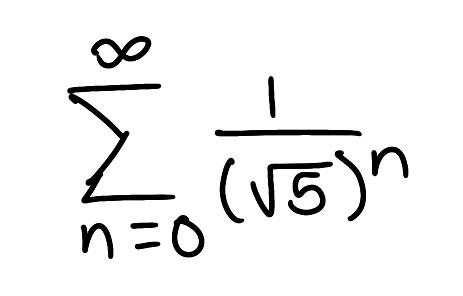
Determine if the series is convergent or divergent. If the series converges, find its sum (if it’s a geometric or telescoping series)

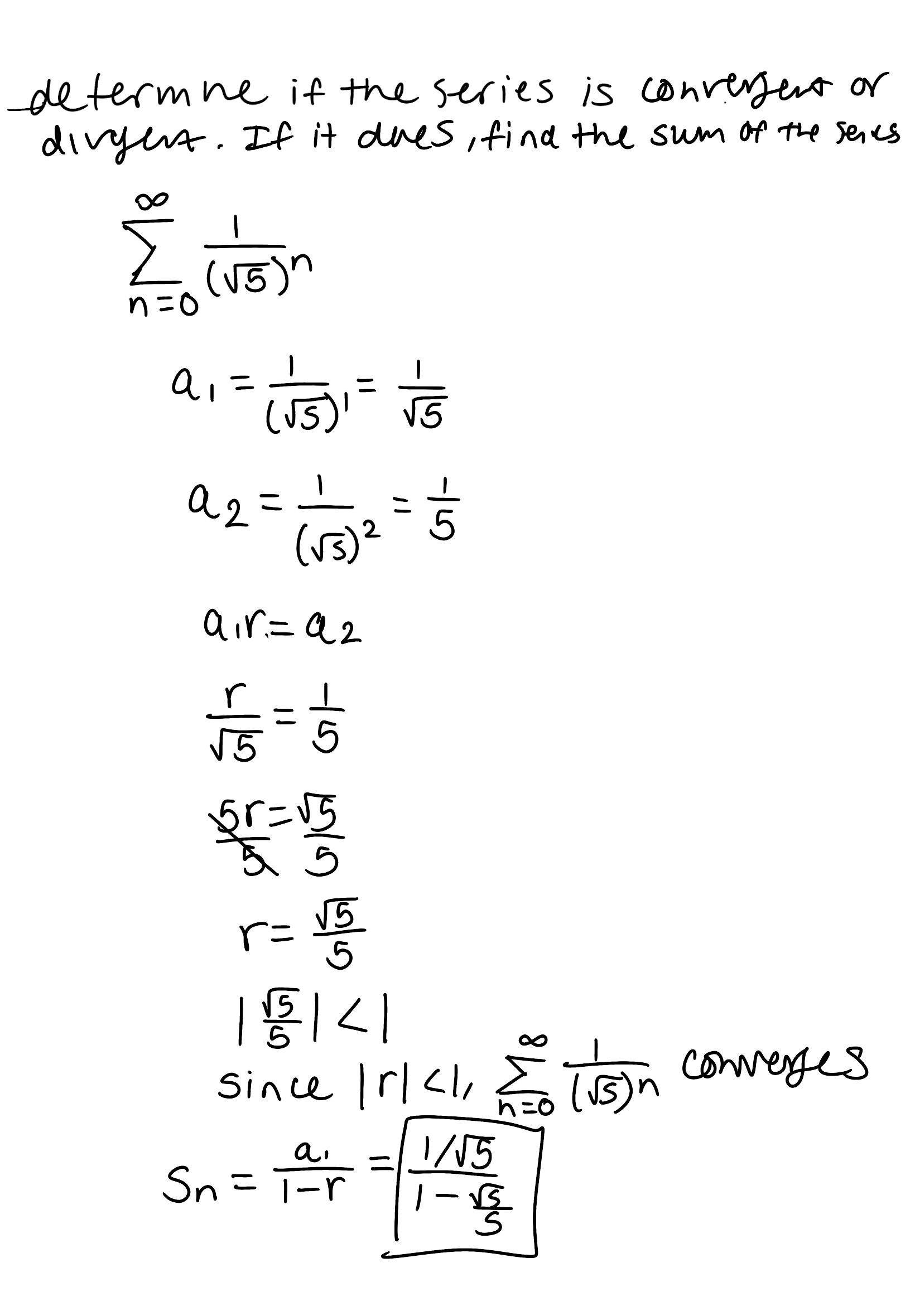
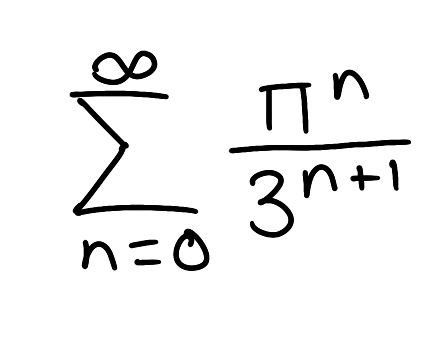
Determine if the series is convergent or divergent. If the series converges, find its sum (if it’s a geometric or telescoping series)

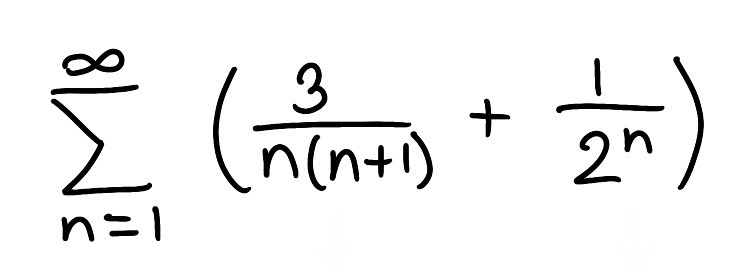
Determine if the series is convergent or divergent. If the series converges, find its sum (if it’s a geometric or telescoping series)

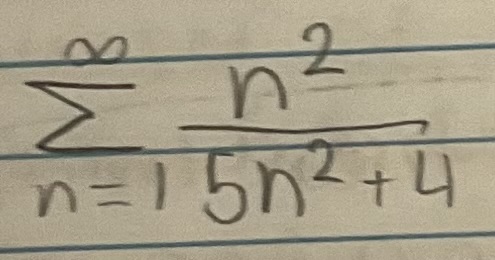
Determine if the series is convergent or divergent. If the series converges, find its sum (if it’s a geometric or telescoping series)

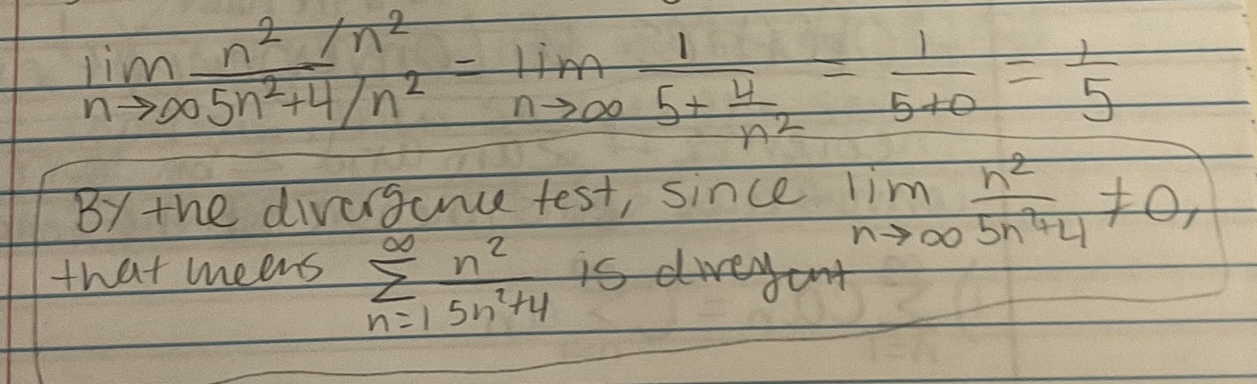
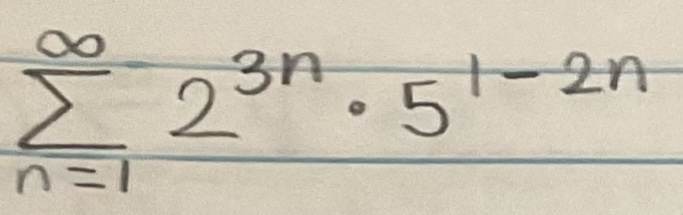
Determine if the series is convergent or divergent. If the series converges, find its sum (if it’s a geometric or telescoping series)

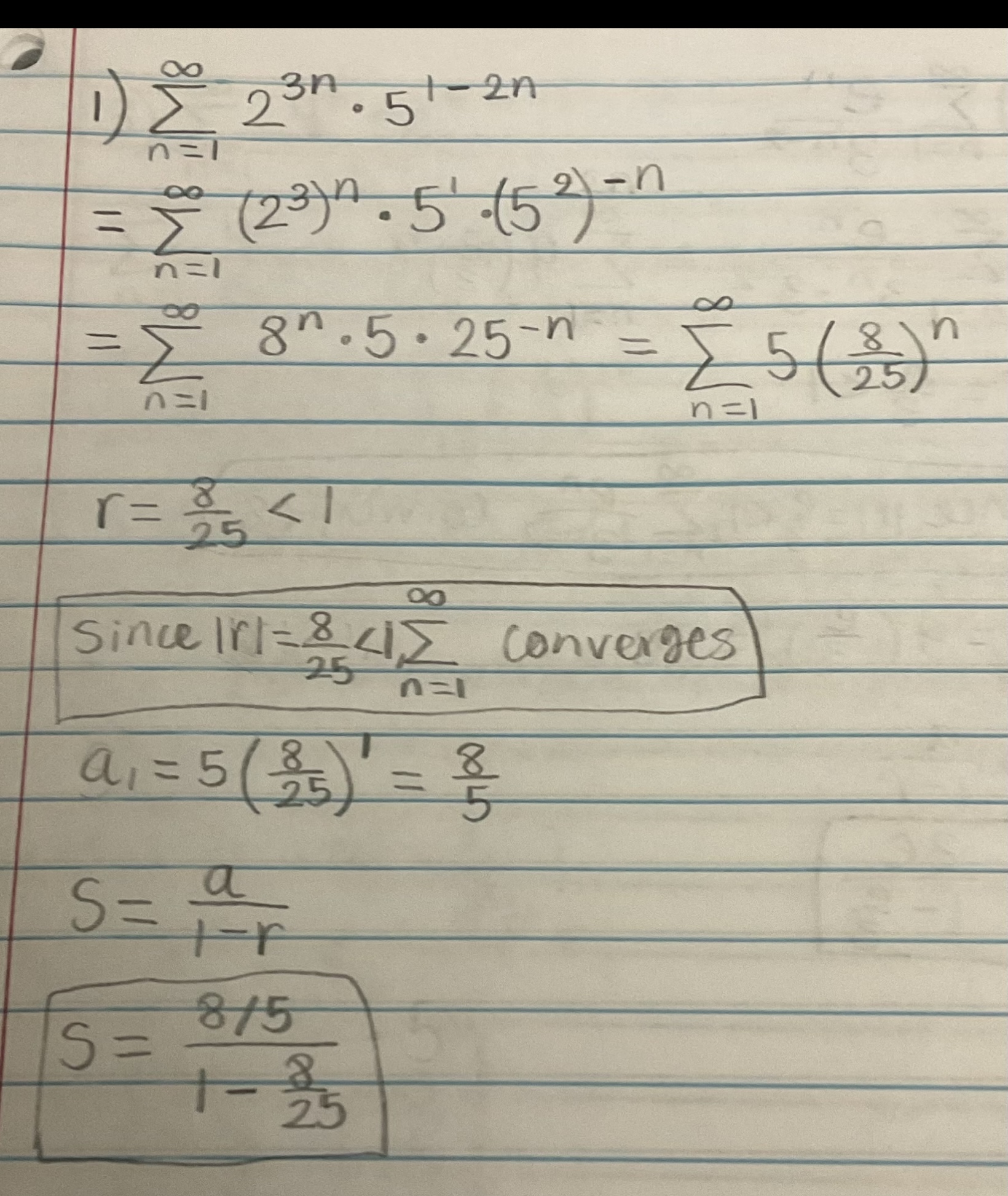
Determine if the series is convergent or divergent. If the series converges, find its sum (if it’s a geometric or telescoping series)

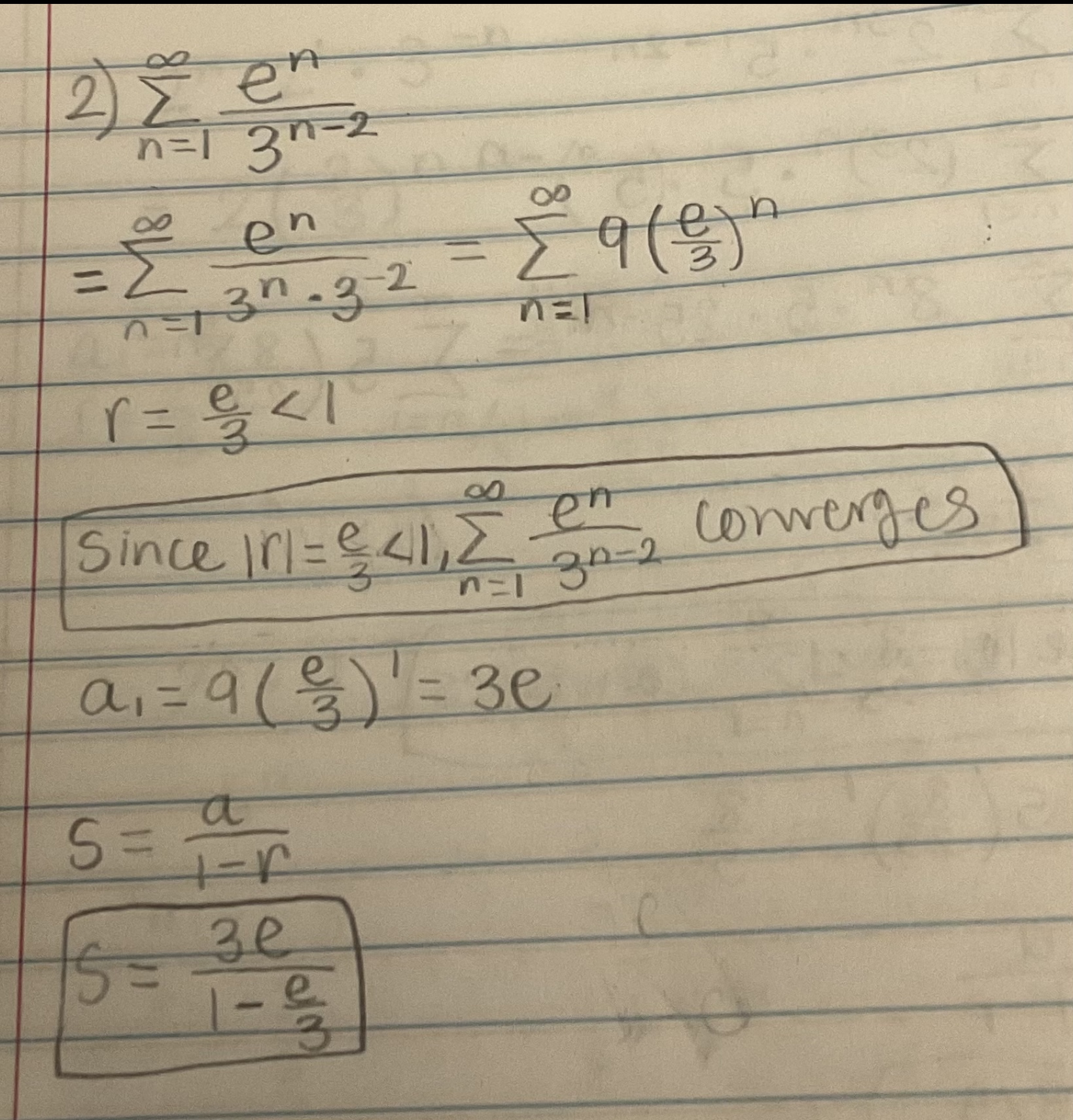
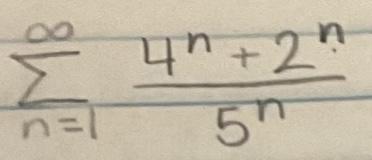
Determine if the series is convergent or divergent. If the series converges, find its sum (if it’s a geometric or telescoping series)

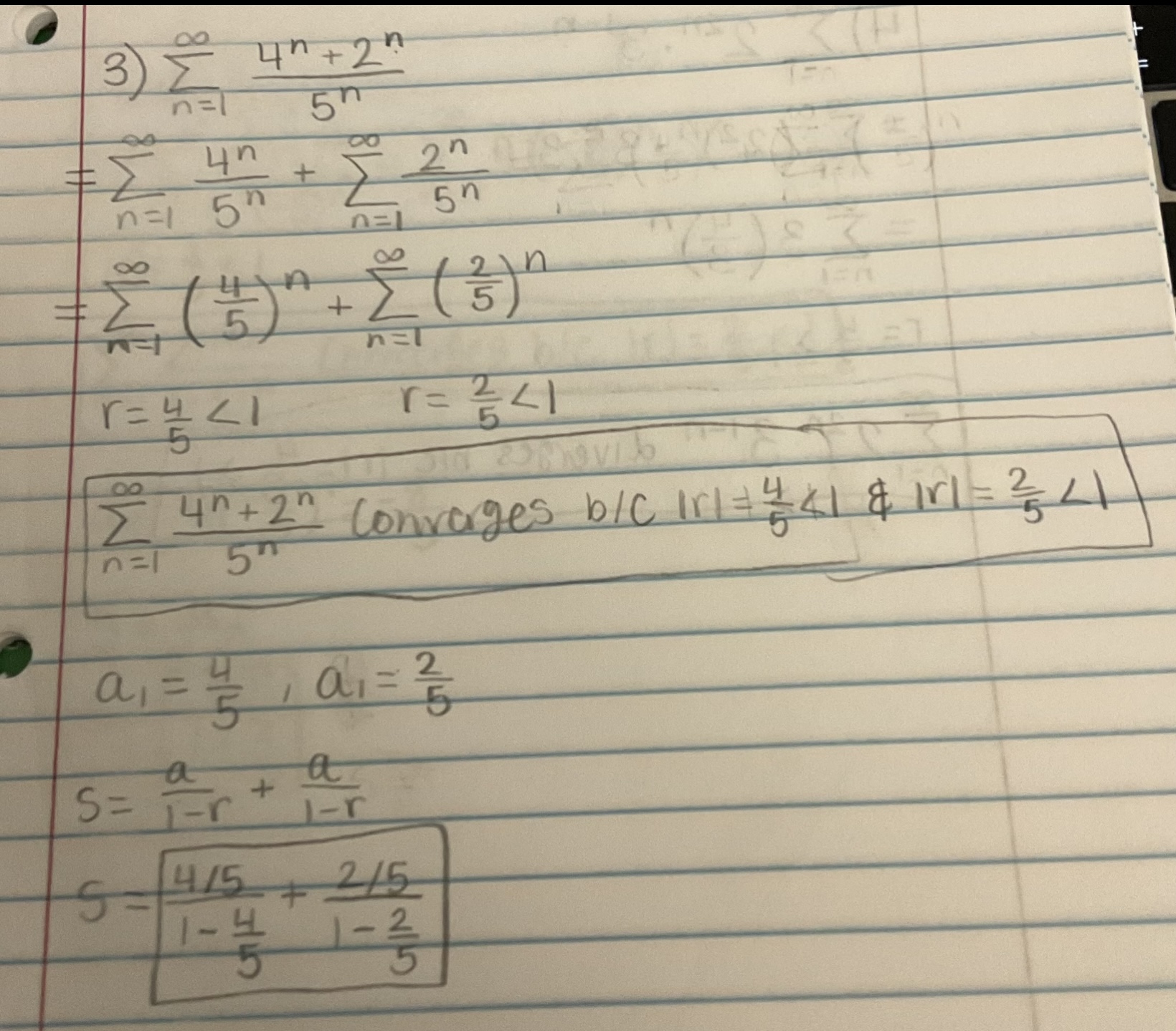
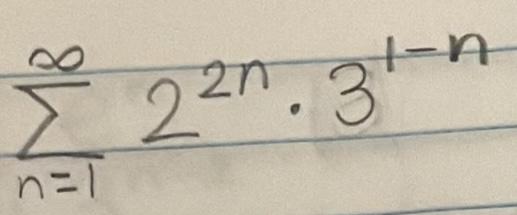
Determine if the series is convergent or divergent. If the series converges, find its sum (if it’s a geometric or telescoping series)

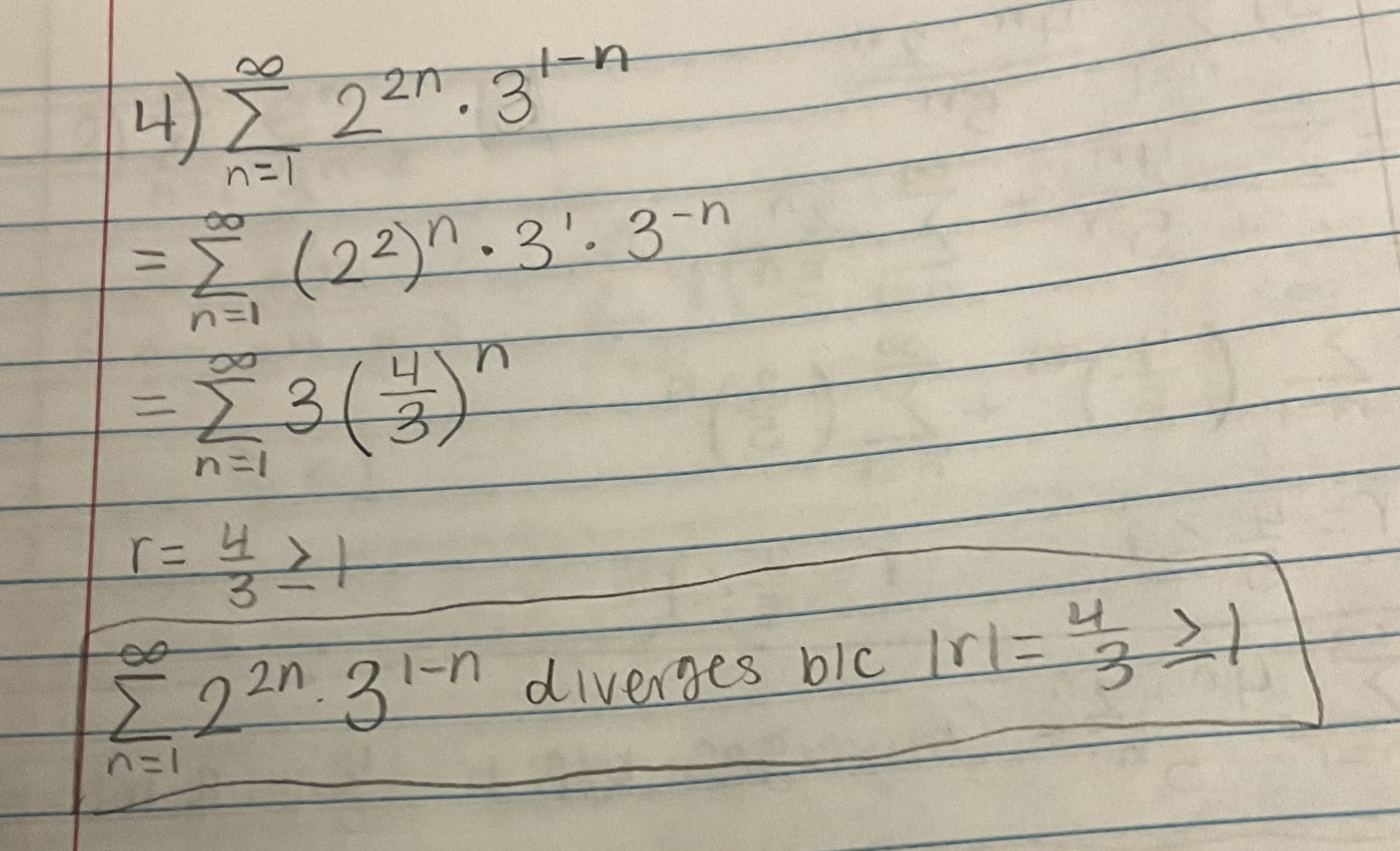
Determine if the series is convergent or divergent. If the series converges, find its sum (if it’s a geometric or telescoping series)