circuits

capacitor

q(t)/v(t)

capacitor current

C*dv(t)/dt

capacitor voltage

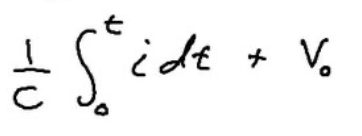
capacitor power

v*i

v*c*dv/dt

capacitor energy

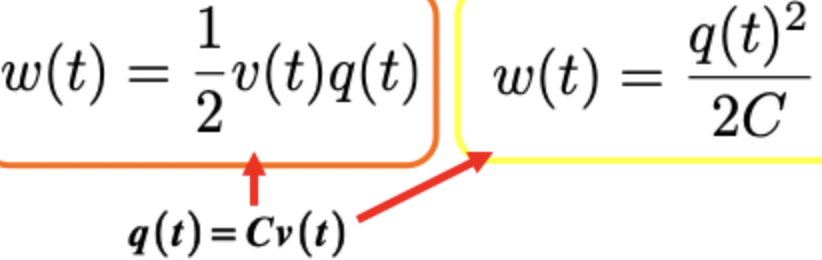
capacitor in parallel

add

capacitor in series

1/ceq = 1/c1 + 1/c2

inductor voltage

v(t) = L* di/dt

inductor current

inductor power

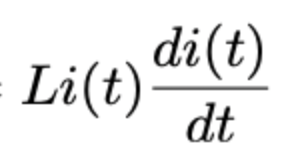
inductor energy

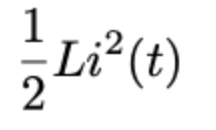
inductor in parallel

like resistors in parallel

inductor in series

add

RC circuit - discharging

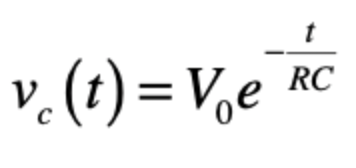
RC circuit - charging

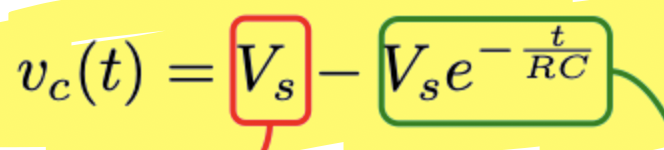
general solution for rc/rl circuits

time constant for capacitor

tao = RC

RL voltage

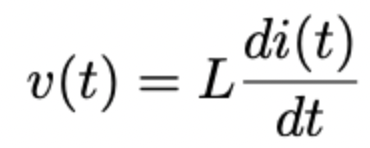
RL circuit current

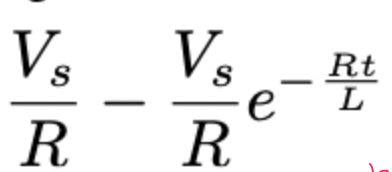
RL time constant

tao = L/R

steady state capacitor

becomes open circuit

steady state inductor

becomes short circuit

steady state initial conditions

no effect on ss behaviour

sinusoidal voltage

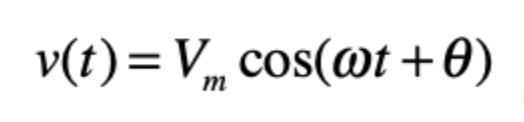
phase angle

tells use delay between v(t) and Vmcost(wt)

finding phase from graph

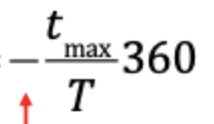
sin(z) sinusoidal manipulation

cos(z-90)

-cos(z) sinusoidal manipulation

cos(z+-180)

time domain

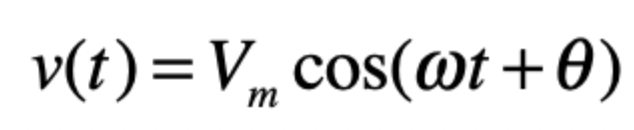
frequency domain

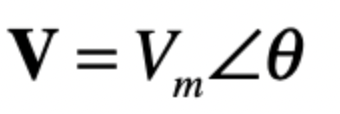
impedance (ohms)

Z=V/I

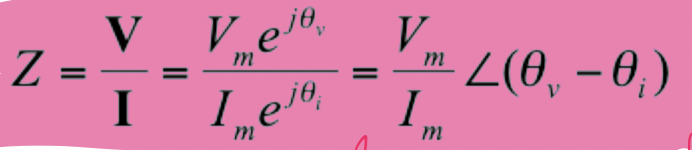
capacitor phasor relationship

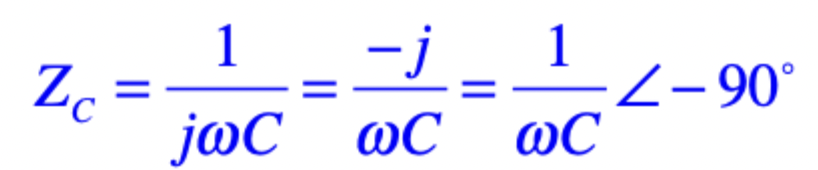
current leads voltage by 90deg

inductor phasor relationship

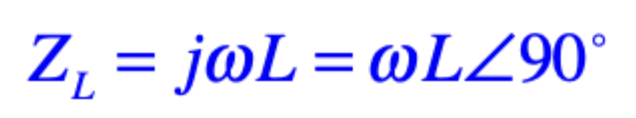
voltage leads current by 90deg

impedance in series

add

impedance in parallel

resistor in parallel

capacitor in ss DC

open circuit

inductor in ss DC

short circuit

Vrms

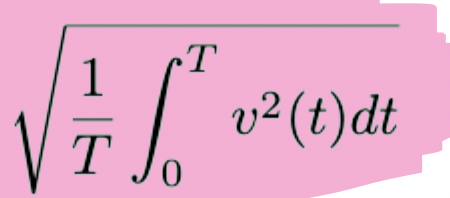
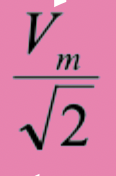
Irms

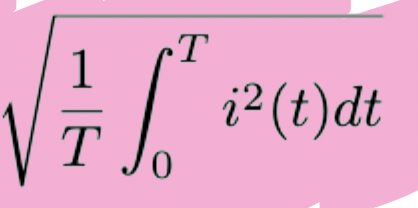
average power, Vrms

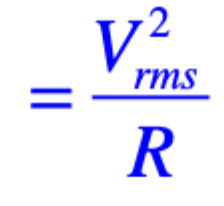
average power, Irms

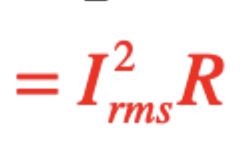
power for resistive load

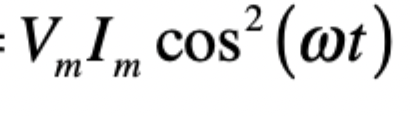
power for inductive load

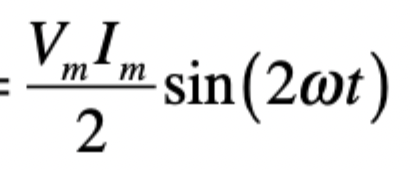
power for capacitive load

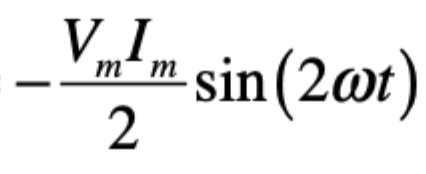
power for a general load

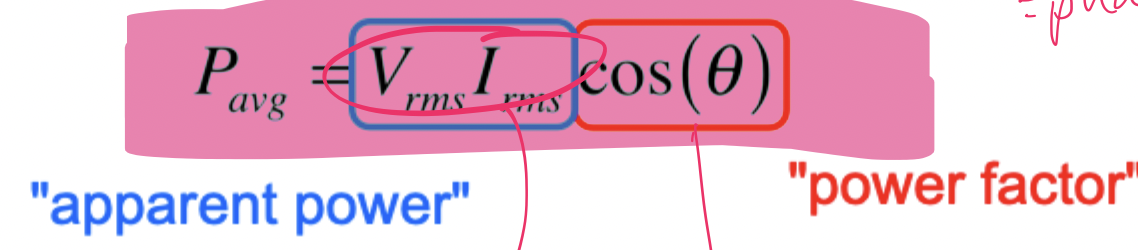
average power = real power = true power

Watts

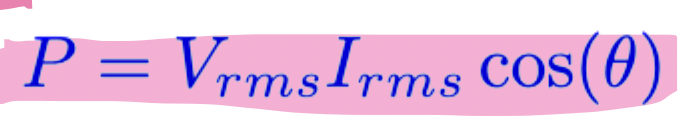
apparent power

VA

reactive power

VAR

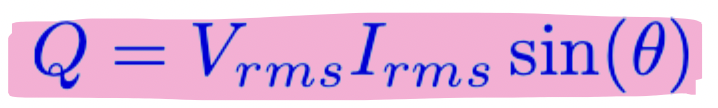
power factor

phase difference bw voltage + current

relationship bw average/apparent/reactive

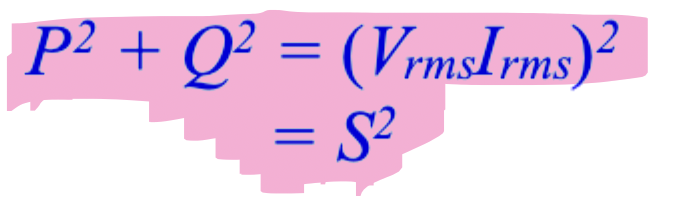
max power transfer for resistive circuits

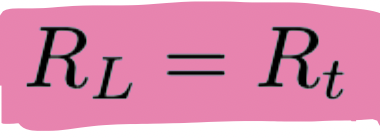
max average power transfer for resistive + reactive circuits

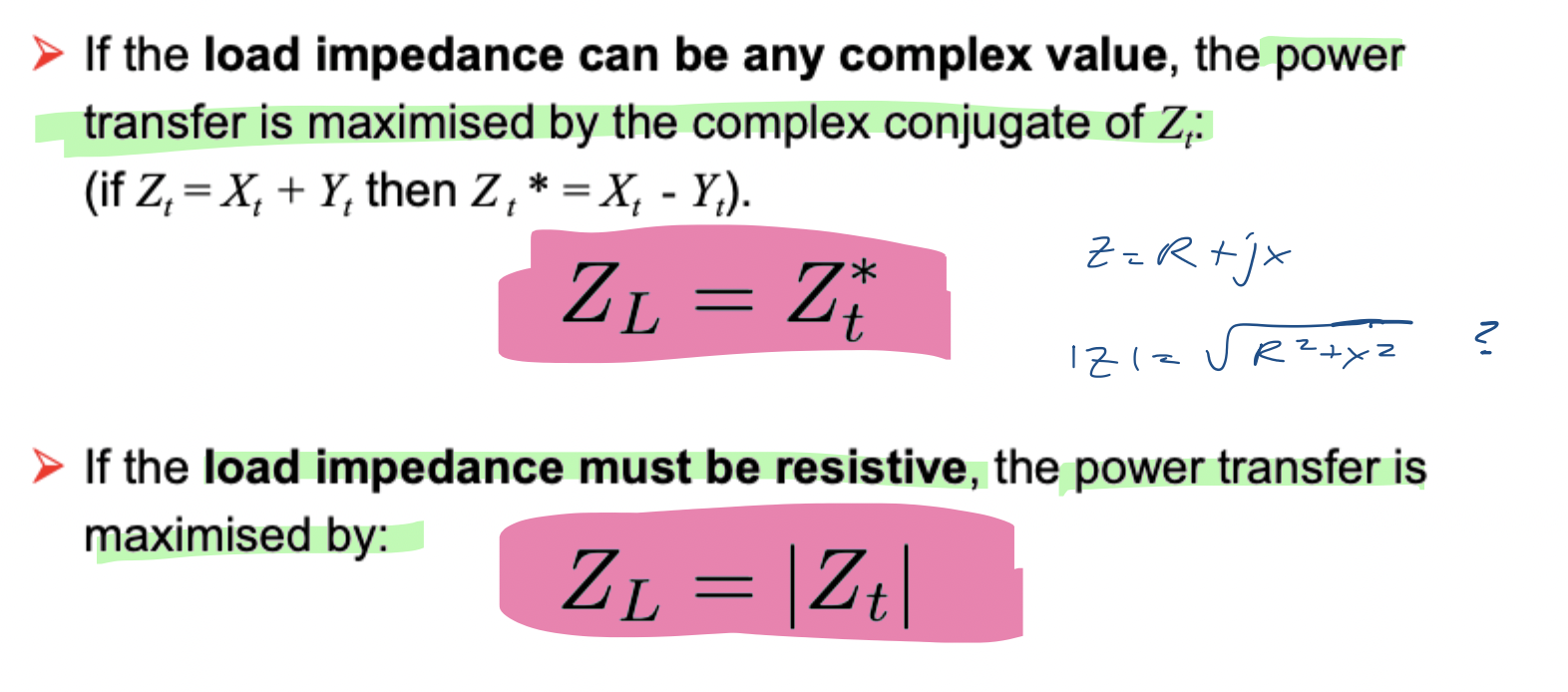
max power transfer current thev

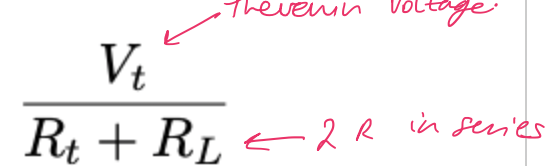
max power transfer power delivered

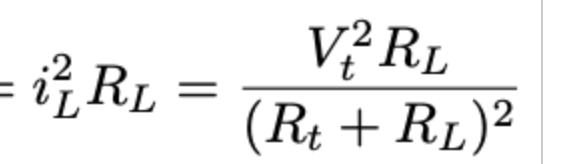
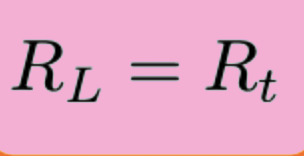
maximum power in thev

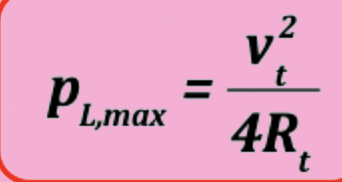
current division

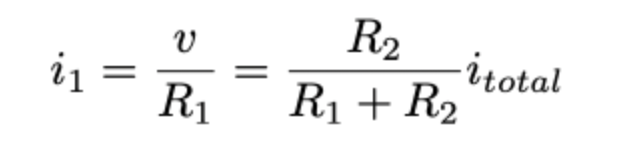
voltage division

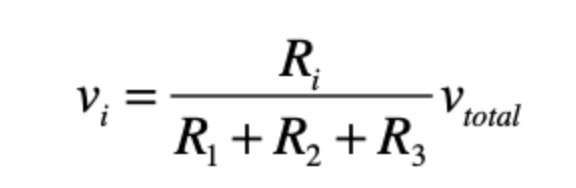
feedback systems - in series

H1(s)H2(s)

feedback systems - in parallel

H1(s) + H2(s)

pole stability - H(s)

eigenvalues negative, in LHP, ≠0

pole stability - H(z)

inside unit circle, less than 1, ≠1