Section 2 - Univariate Distributions

Discrete versus Continuous

Discret: A set of countable values

ex: {1,2,3,…}

Continuous: Values in intervals

ex: (0,100)

Probability Function for a Continuous Random Variable and conditions

• Probability Density Function (PDF) → not equal to Pr(X=x) since it can take on an infinite number of values

• Denoted as f(x), fx(x)

What is a Discrete Uniform Distribution and its criteria?

1) Finite Number of possible values

2) Consecutively spaced by 1 (ex: 1,2,3,...,10 inclusive)

3) Equally likely to be observed

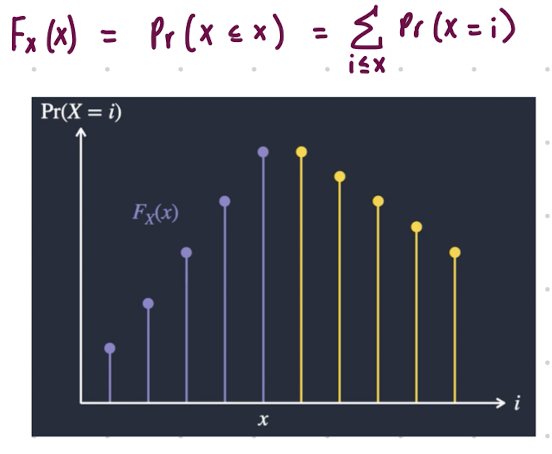
Cumulative Distribution Function (CDF) for a Discrete Random Variable

• Denoted as P(X ≤ x), F(x), Fx(x)

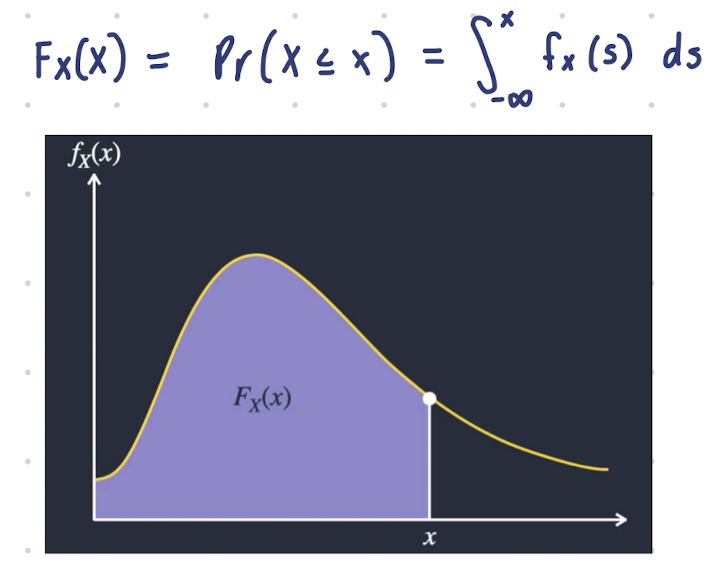
Cumulative Distribution Function (CDF) for a Continuous Random Variable

• Denoted as P(X ≤ x), F(x), Fx(x)

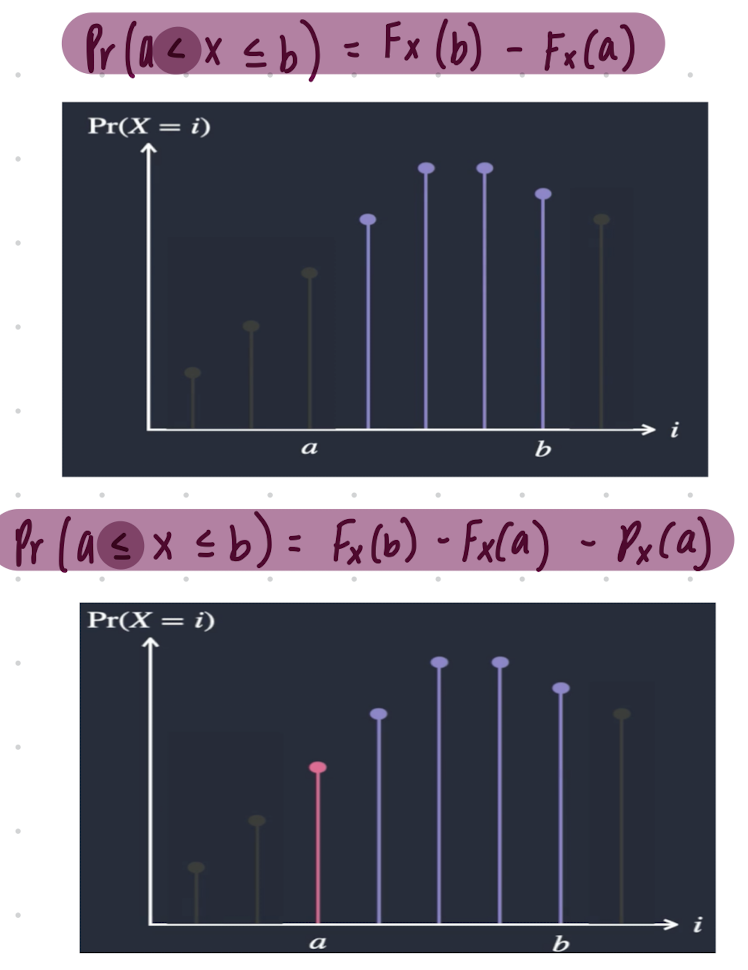
What are the two important formulas to know for a CDF for a discrete random variable?

How do we calculate the CDF probabilities for a continuous random variable?

What are the properties of a CDF for a Discrete Random Variable?

1) Non-decreasing

2) Fx(-∞) = 0, Fx(∞) = 1

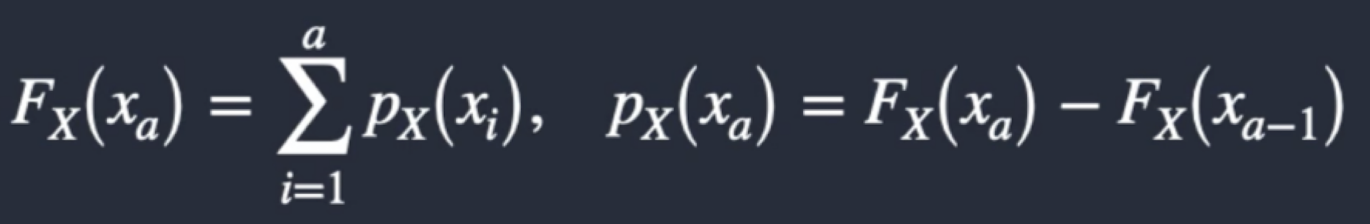
What are the properties of a CDF for a Continuous Random Variable?

1) Non-decreasing

2) Fx(-∞) = 0, Fx(∞) = 1

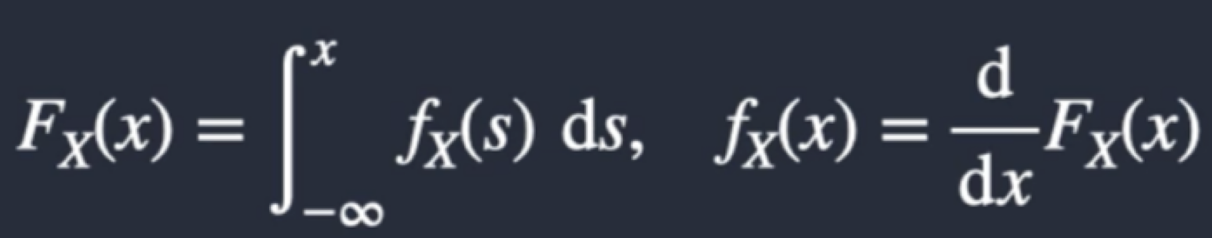
What is the survival function for a discrete random variable?

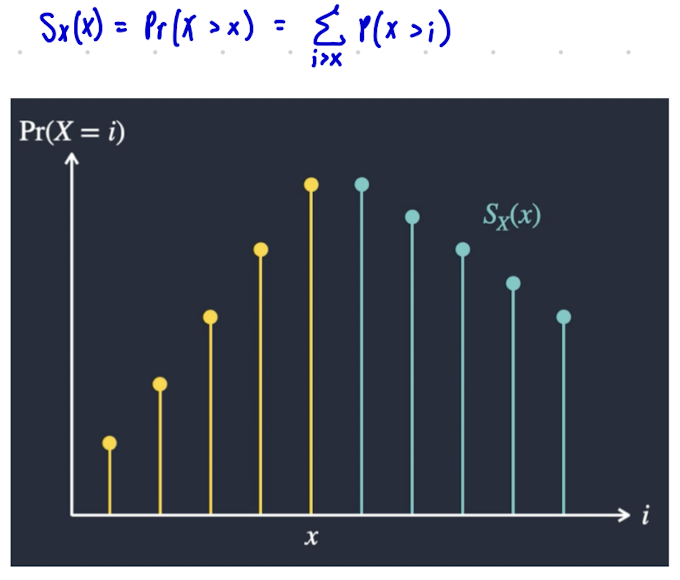
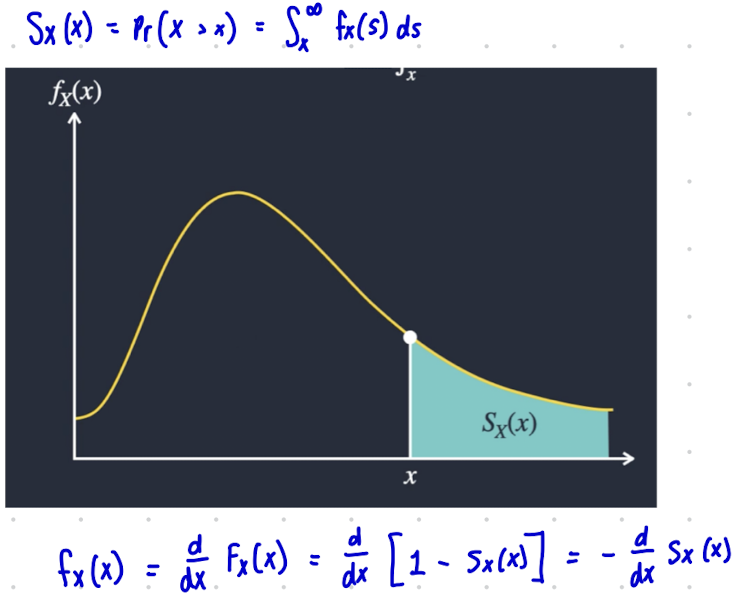
What is the survival function for a continuous random variable?

Hazard Rate Function

• Only for continuous random variables

• Likely not tested on the exam

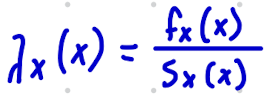
What are mixed distributions?

1) Multiple distinct, discrete distributions

1) Multiple distinct, continuous distributions

1) A combination of discrete and continuous distributions

What are the 2 ways to understand a mixed distribution?

1) Focus on the individual distribution separately

2) View the mixed distribution as a whole

Definition: Expected Value

• Also called the mean, expectation, or first moment

• Denoted as E[x]

What is the expected value for a discrete random variable?

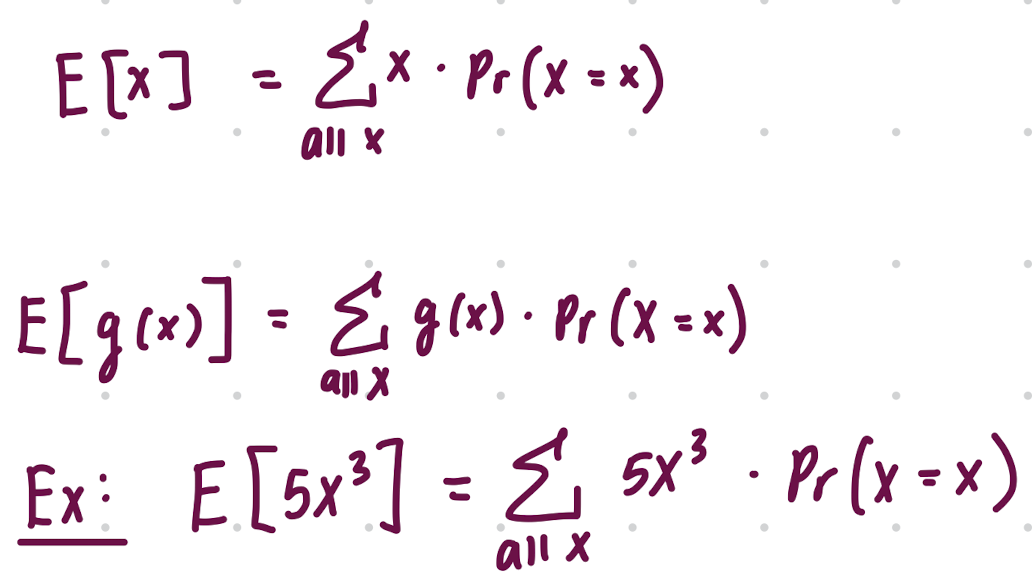
What is the expected value for a continuous random variable?

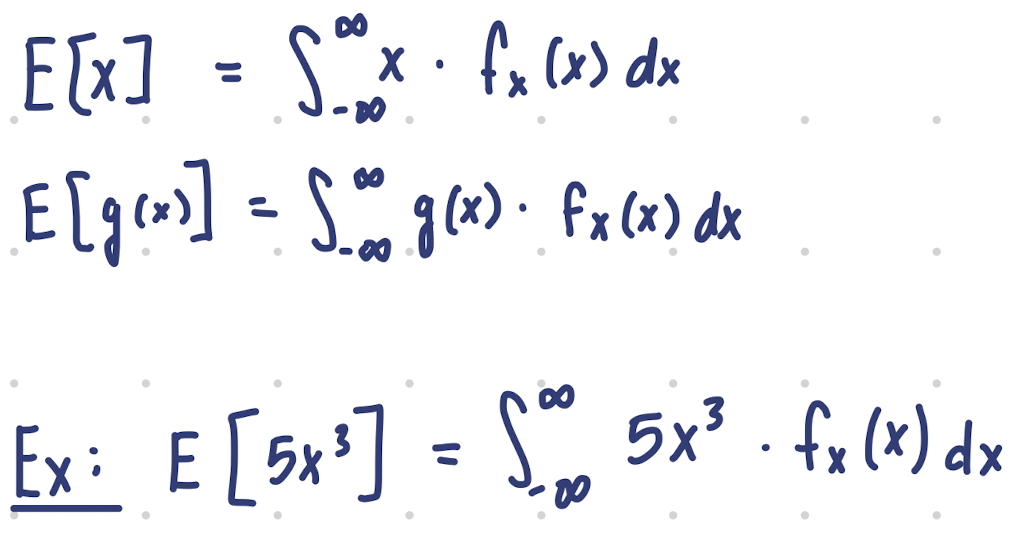
What are the 3 key properties for an exoected value?

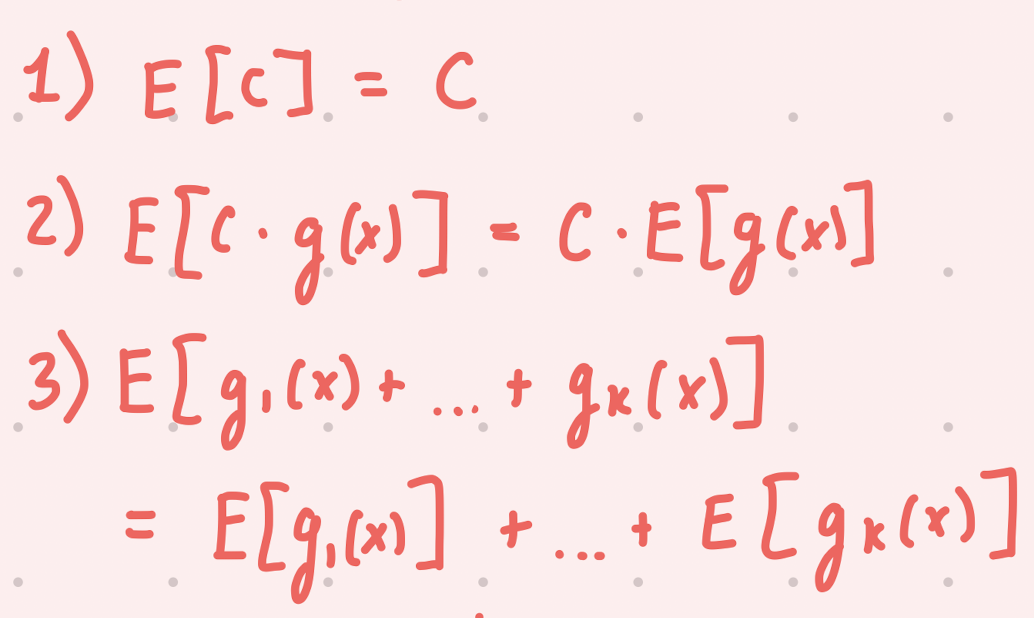
What do we do if there is a mixed distribution?

• Use intuitive and reasoning

• If piecewise, split sum/integral wherever fx(x) for g(x) changes

What is the conditional expectation for a discrete random variable?

• Use the same general approach

• Use conditional probabilities and conditional ranges

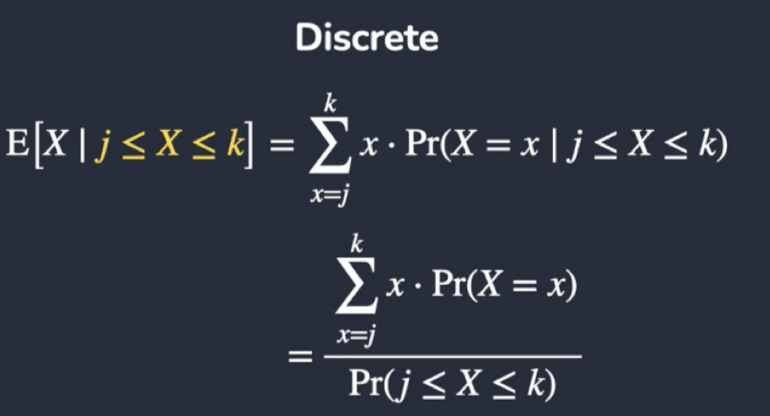
What is the conditional expectation for a continuous random variable?

• Use the same general approach

• Use conditional probabilities and conditional ranges

What is the conditional PDF?

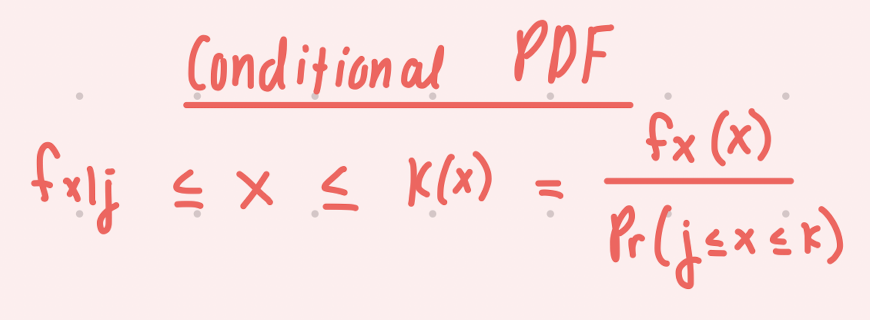
Survival Function method for Discrete Random Variables

• Alternative to Probability Function Method

• Can only use if the range is non-negative

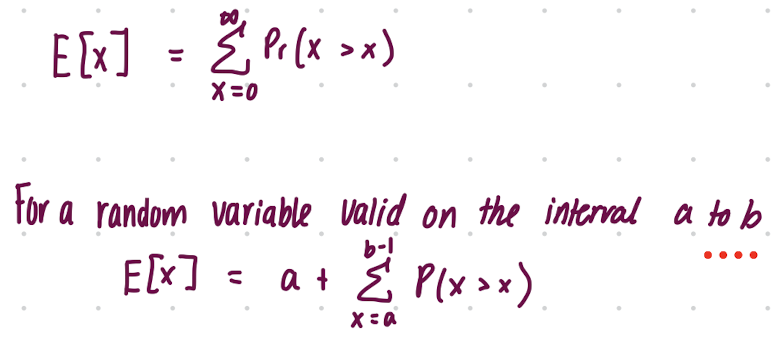
Survival Function method for Continuous Random Variables

kth and 1st Raw Moment

kth and 2nd central moment

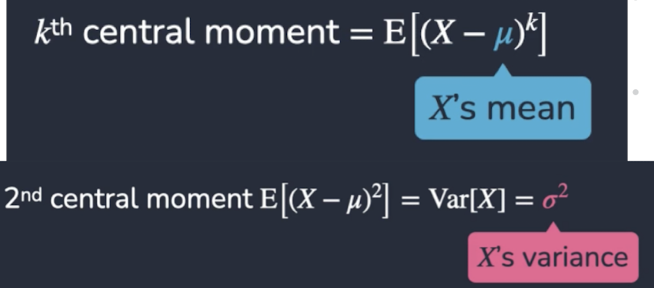
Definition: Variance

Average squared deviation from the mean

Variance Equations for x and g(x)

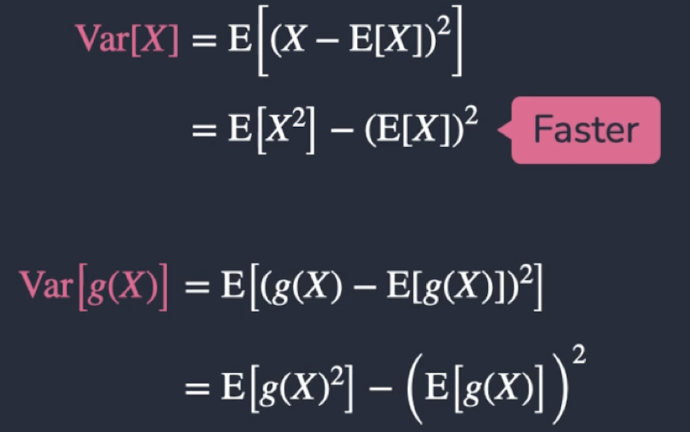
Properties for variance

Coefficient of Variation

Measures variability of a random variable

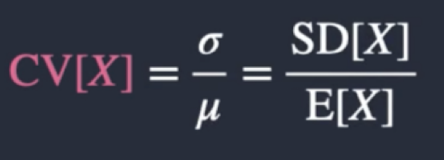
Percentiles

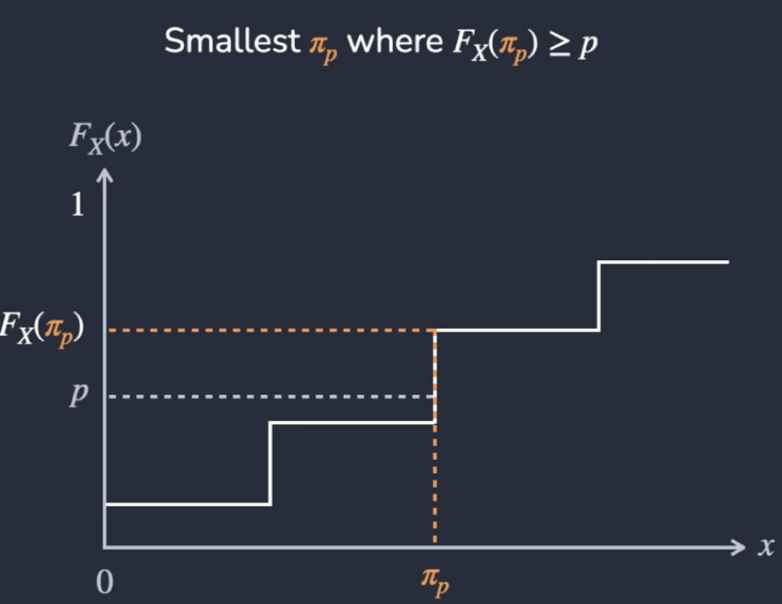
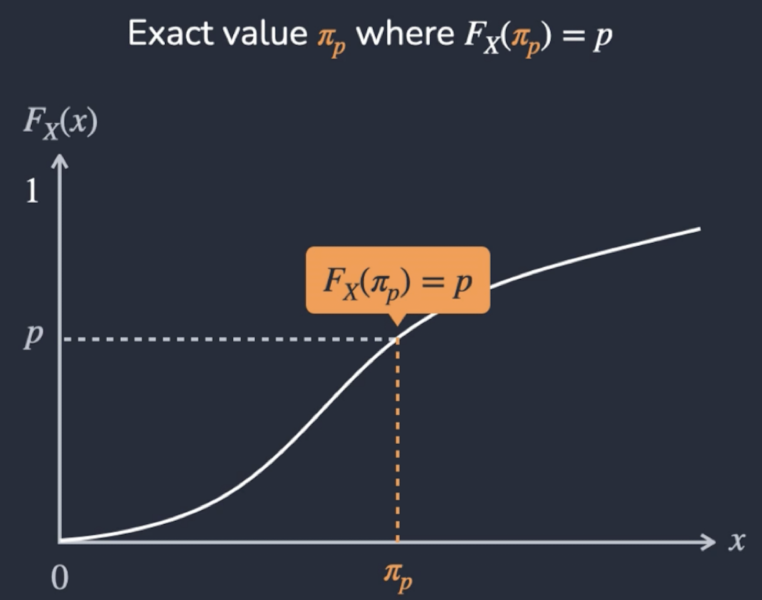
• πp = 100th Percentile

• Pr(x ≤ πp) = p

• πp​ is the percentile value such that the cumulative probability up to that value is p

Percentile for Discrete Random Variables

Percentile for Continuous Random Variables

What are the common percentiles and IQR?

What is the mode for discrete random variables?

• Most likely values of a random variable

• Value of x maximizes the PMF/PDF

• The highest value for px(x) is the mode

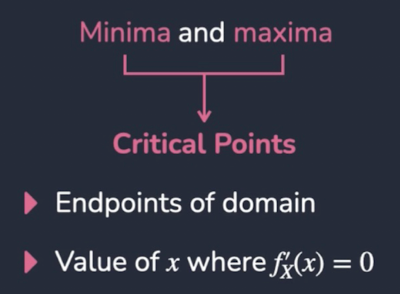
What is the mode for continuous random variables?

• Critical Point with largest value of fx(x)

Skewness: Equation

• Measures a distributions symmetry

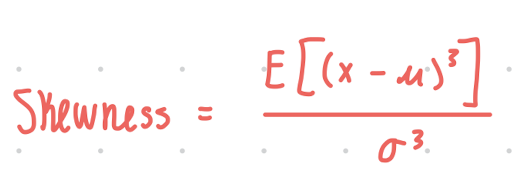
What is zero skewness, positive skewness and negative skewness?

Kurtosis: Equation

• Measures the “peakedness” of a distribution

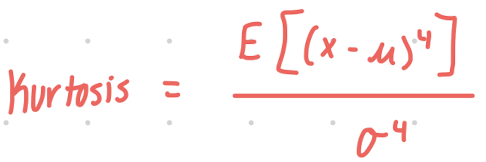
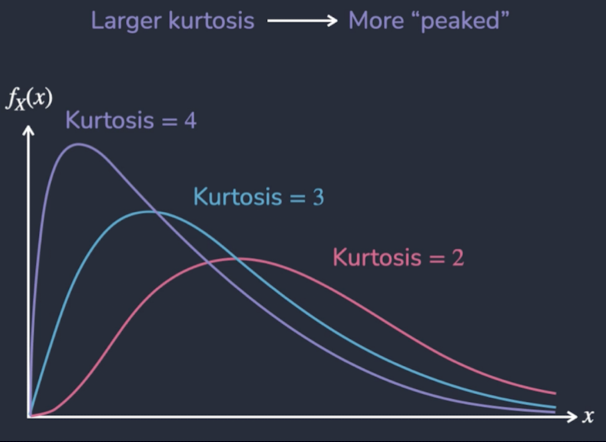
What do the different levels of kurtosis mean?

What is an example of a discrete uniform distribution?

1) Rolling a fair die

2) The number of customers that visit a store during a workday is uniform on {20,21,...,80}

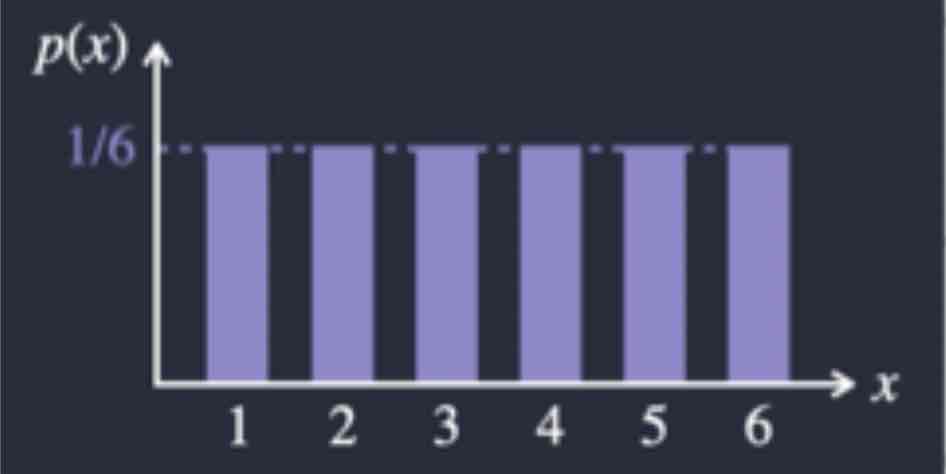
What are the parameters of a discrete uniform distribution?

x ~ Discrete Uniform(a,b)

a and b are the parameters

What is the PMF of a discrete uniform distribution?

What is the Expected Value (mean) of a discrete uniform distribution?

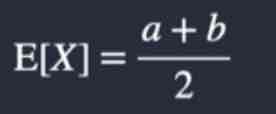
What is the Variance of a discrete uniform distribution?

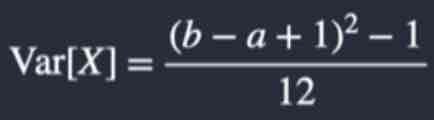
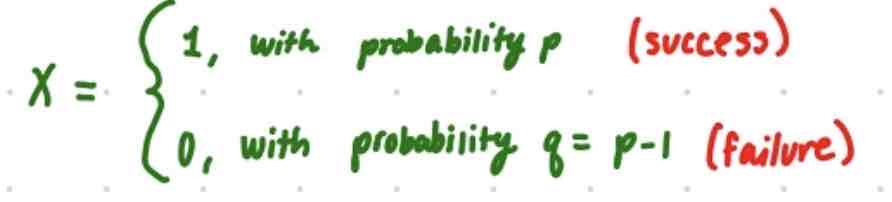
What is a Bernoulli distribution and its criteria?

1) 2 possible outcomes, 0 and 1

2) 0 and 1 can be any binomial event

What is an example of a Bernoulli distribution?

A coin flip would be Bernoulli if we assign 1 to heads and 0 to tails and vice versa

What if the PMF of a Bernoulli distribution?

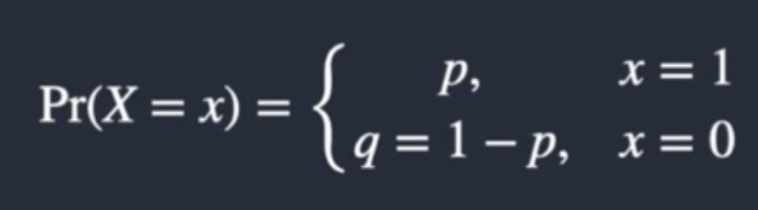
What if the mean of a Bernoulli distribution?

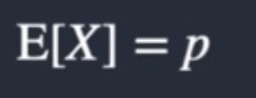
What is the Variance of a bernoulli distribution?

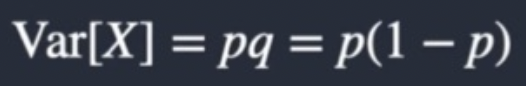
What is the Bernoulli Shortcut?

If we have an event with only 2 outcomes (a and b) then we can use this

What are the parameters of a Bernoulli Distribution?

x ~ Bernoulli (p)

Parameter is p

What are the parameters of a Binomial Distribution?

x ~ binomial(n,p)

n and p are the parameters

What is a Binomial Distribution and its criteria?

- The sum of n independent Bernoulli Trials with the probability of success p

- Counts the number of successes

What is an example of a Binomial Distribution?

Tossing a coin 5 times and counting the number of heads in those 5 trials

How can you identify a binomial distribution?

1) Fixed number of independent trials

2) Same 2 possible outcomes for each trial

3) Number of sccesses (varies) is the random variable

How can you identify independent trials? (2 ways)

1) sampling with replacement

2) Sampling without replacement from a large population of unknown size (while population changes, the impact on each trial is small - treat the population as staying the same)

What would dependent trials look like?

Sampling without replacement of a known population size

What is the PMF for a binomial distribution?

What is the expected value for a binomial distribution?

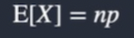
What is the variance for a binomial distribution?

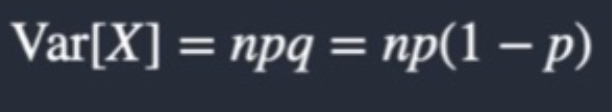
What is the special property for the sum of a binomials?

What is a Hypergeometric Distribution and its criteria?

1) Same situation as binomial but with DEPENDENT Bernoulli Trials

2) Sampling WITHOUT replacement from a KNOWN population size

What are the parameters for a hypergeometric distribution and what do they mean?

x ~ Hypergeometric (N, m, n)

N is the population size

m is the successes in a population

n is the number of dependent trials

What is the PMF of a hypergeometric distribution?

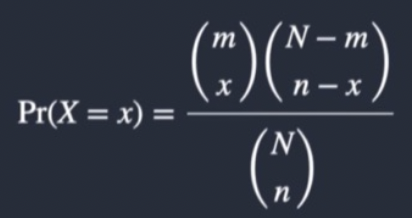
What is the Expectation of a hypergeometric Distribution?

What is the Variance of a hypergeometric Distribution?

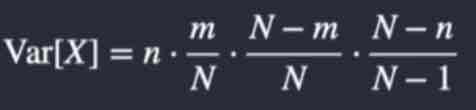
What other technique can we use to solve hypergeometric questions?

Counting techniques!

What is a Geometric distribution and its criteria?

The number of independent bernoulli trials when we want to get the FIRST success

1) Fixed number of successes

2) Variable number of trials

What is an example of a geometric distribution?

The number of coin tosses it takes to get the first “heads”

How can we identify a geometric distribution?

1) Indepenedent bernoulli trials

2) Same two possible outcomes for each trials

3) Random variable is the number of trials/failues to get to ONE SUCCESS

2) Number of trials or failures? (“Number of trials before the first success” → number of failures)

What is the parameter for a geometric distribution?

x ~ geometric(p)

p: probability of a success

What is the trial version PMF of a geometric distribution?

X = Number of Trials to get one Success

What is the trial version Expectation of a geometric distribution?

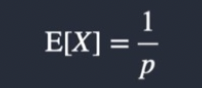
What is the trial version variance of a geometric distribution?

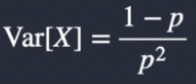
What is the Failure version PMF of a geometric distribution?

Y = Number of Failures before one success

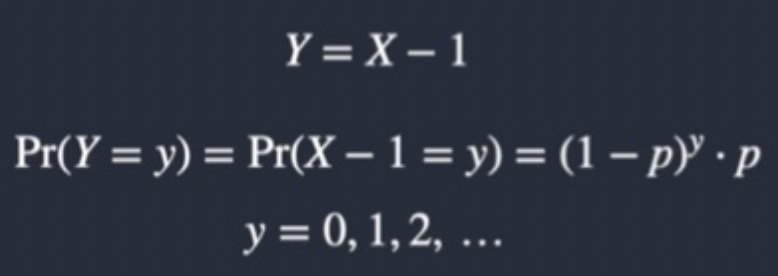
What is the Failure version Expectation of a geometric distribution?

What is the failure version Variance for a geometric distribution?

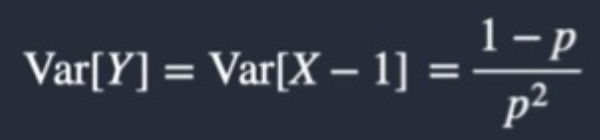
What is the memoryless property for the trial version of a geometric distribution?

• The outcomes of previous trials do NOT affect the probabilities of future trials

• Consider every new trial as the first trial

What is the memoryless property for the failure version of a geometric distribution?

• The outcomes of previous trials do NOT affect the probabilities of future trials

• Consider every new trial as the first trial

What are the is the definition and parameters for a negative binomial distribution?

x ~ Negative Binomial(r,p)

The number of trials to get r successes, where each trial has a success probability of p

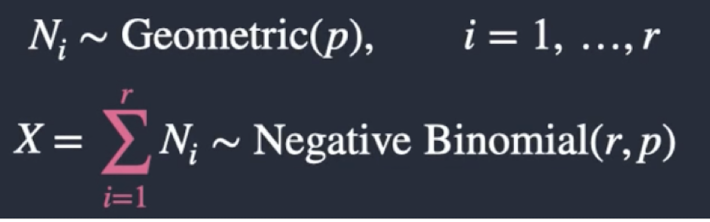
What is the failure version expectation of a negative binomial distribution?

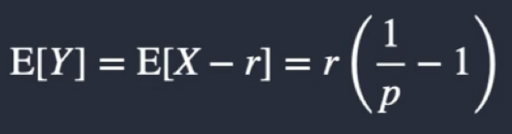
What is an exmaple of a negative binomial distribution?

The number of coin tosses required to ger 5 “heads”

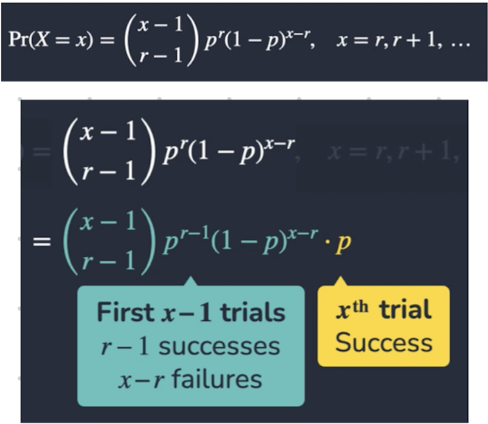
What is the trial version PMF of a negative binomial distribution?

What is the trial version expectation of a negative binomial distribution?

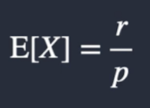
What is the trial version variance of a negative binomial distribution?

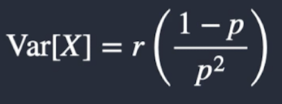
What is the special property for negative binomials?

What is the failure version PMF of a negative binomial distribution?

What is the failure version Variance of a negative binomial distribution?

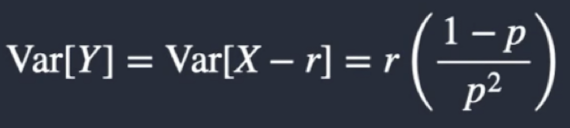
How can you identify a negative binomial distribution?

1) Independent bernoulli trials

2) Random variable is the number of trials/failures to get a certain number of successes

• Fixed number of successes, r

• Variable number of trials/variables

What is a poisson distribution?

• Number of events in a fixed interval

• Occurences in disjoint intervals are independent

• Interval is usually time but it can be something else

What is an example of a poisson distribution?

• The number of tornados in a field during a year

• Count the number of flowers in a square foot of a field

What is the parameter of a poisson distribution?

x ~ poisson(λ)

λ (lambda) is the parameter, it is the mean (event rate)

What is the PMF of a poisson distribution?

• Typically told to use poisson

• Recognize from PMF

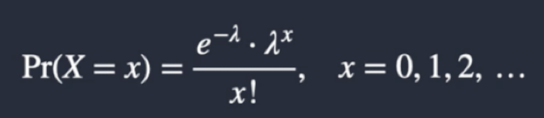
What is the expectation of a poisson distribution?

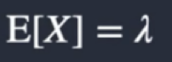
What is the variance of a poisson distribution?

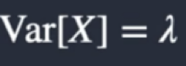
What are the 2 properties of a poisson distribution?

What is a continuous uniform distribution?

• DO NOT CONFUSE WITH DISCRETE DISTRIBUTIONS

• Equal-length intervals are equally likely

• Infinite number of possible values (any value between a and b)

• say the time to drive to work is between 8 and 12 minutes

• Probability between 8 and 9 minutes, 9 and 10 minutes, 10 and 11 minutes, and 11 and 12 minutes are all the same

What are the parameters of a and b?

x ~ continuous uniform(a,b)

a is the smallest value, b is the largest value

What is the PDF of a continuous uniform distribution?