Calculus I- Theorems and Equations Study Guide

(a,b)

{x: a<x<b}

“open interval from a to b”

[a,b]

{x: a≤x≤b}

“closed interval from a to b”

b⁰

=1

b^xb^y

=b^x+y

(b^x/b^y)

=b^x-y

(b^x)^y

=b^xy

b^1/n

=n^th root(b)

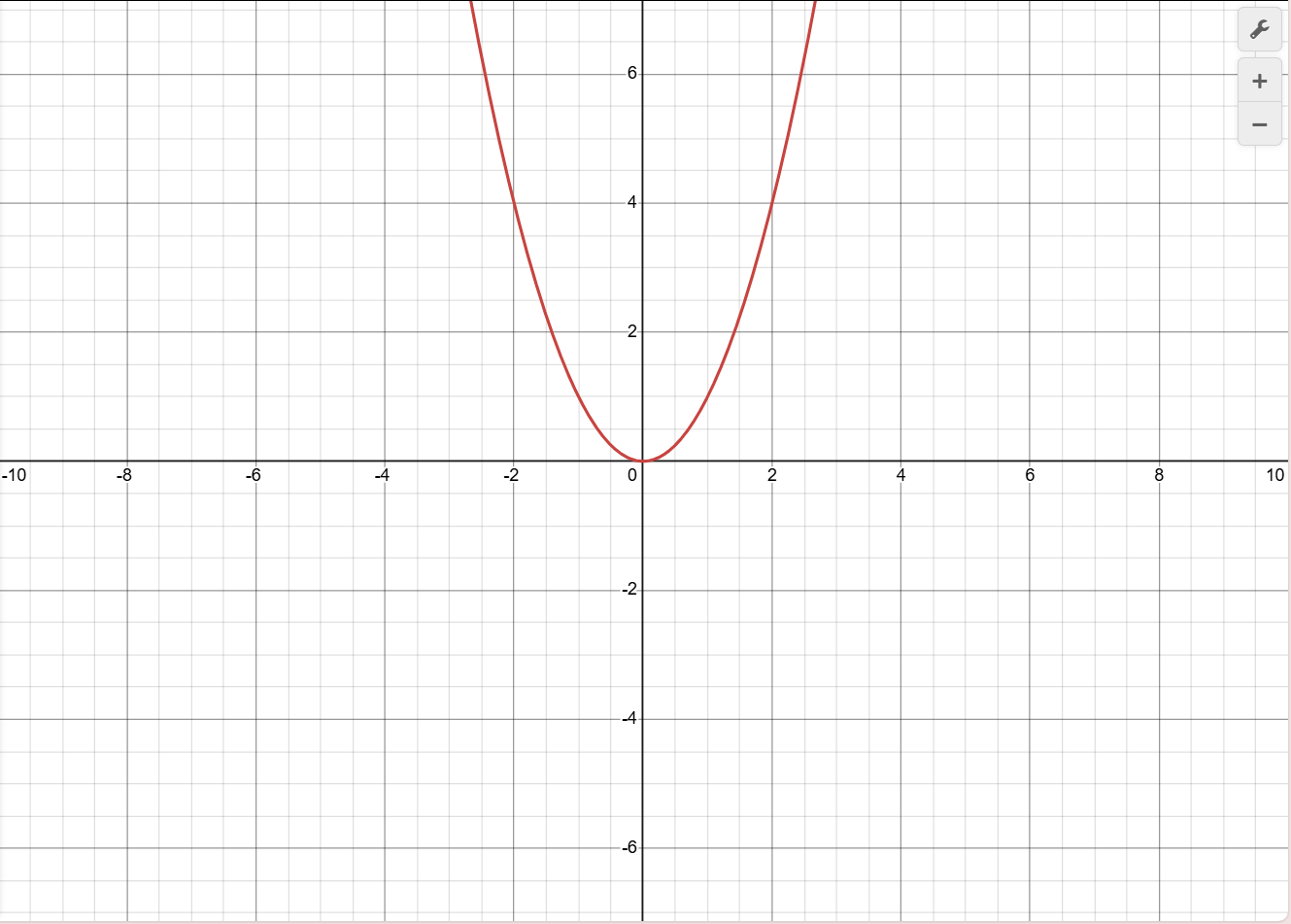
y=x²

Domain (-∞, ∞)

Range [0, ∞)

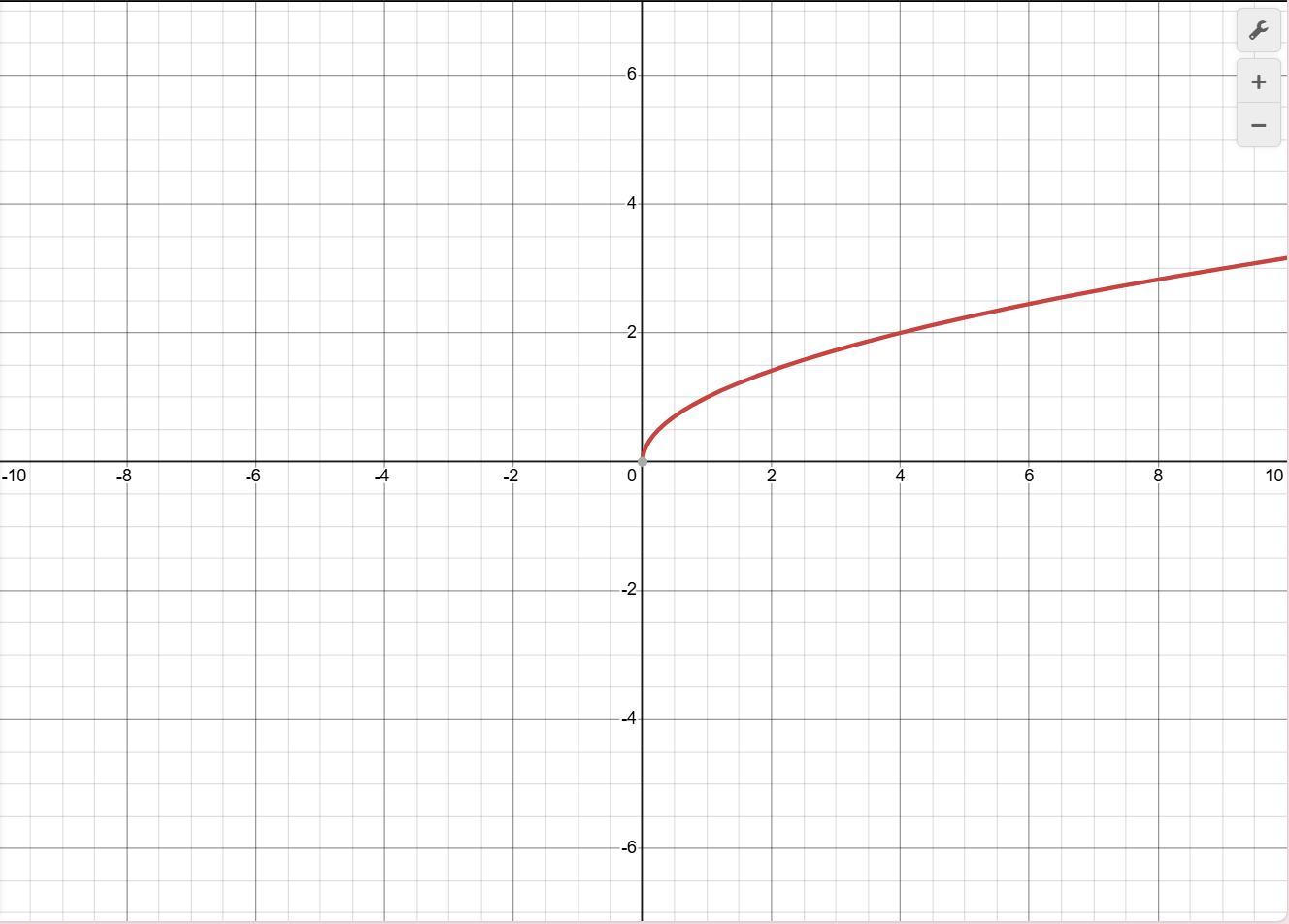
y=rt(x)

Domain [0, ∞)

Range [0, ∞)

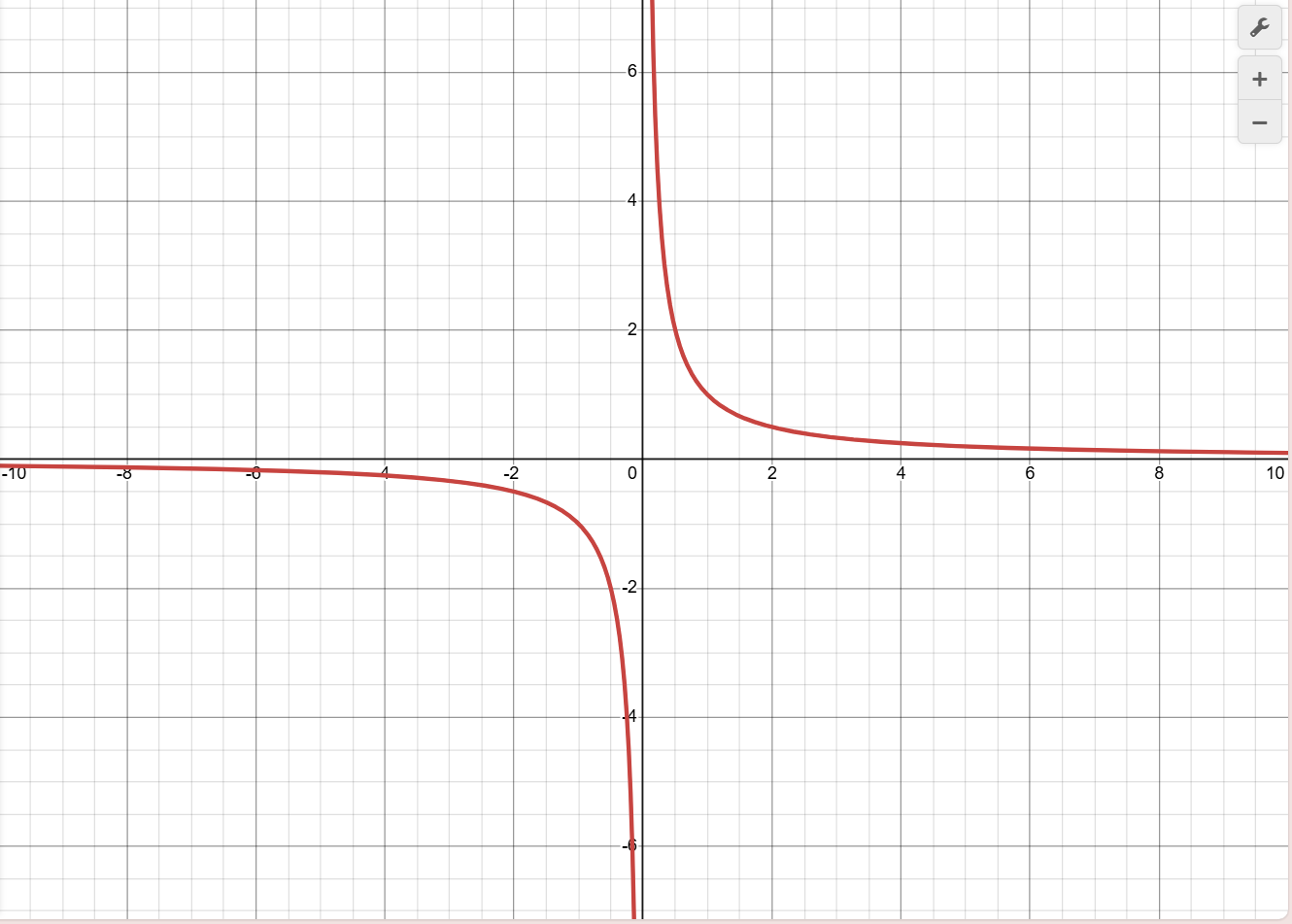
y=(1/x)

Domain (-∞, 0) u (0, ∞)

Range (-∞, 0) u (0, ∞)

x²+y²=1

Domain [-1, 1]

Range [-1, 1]

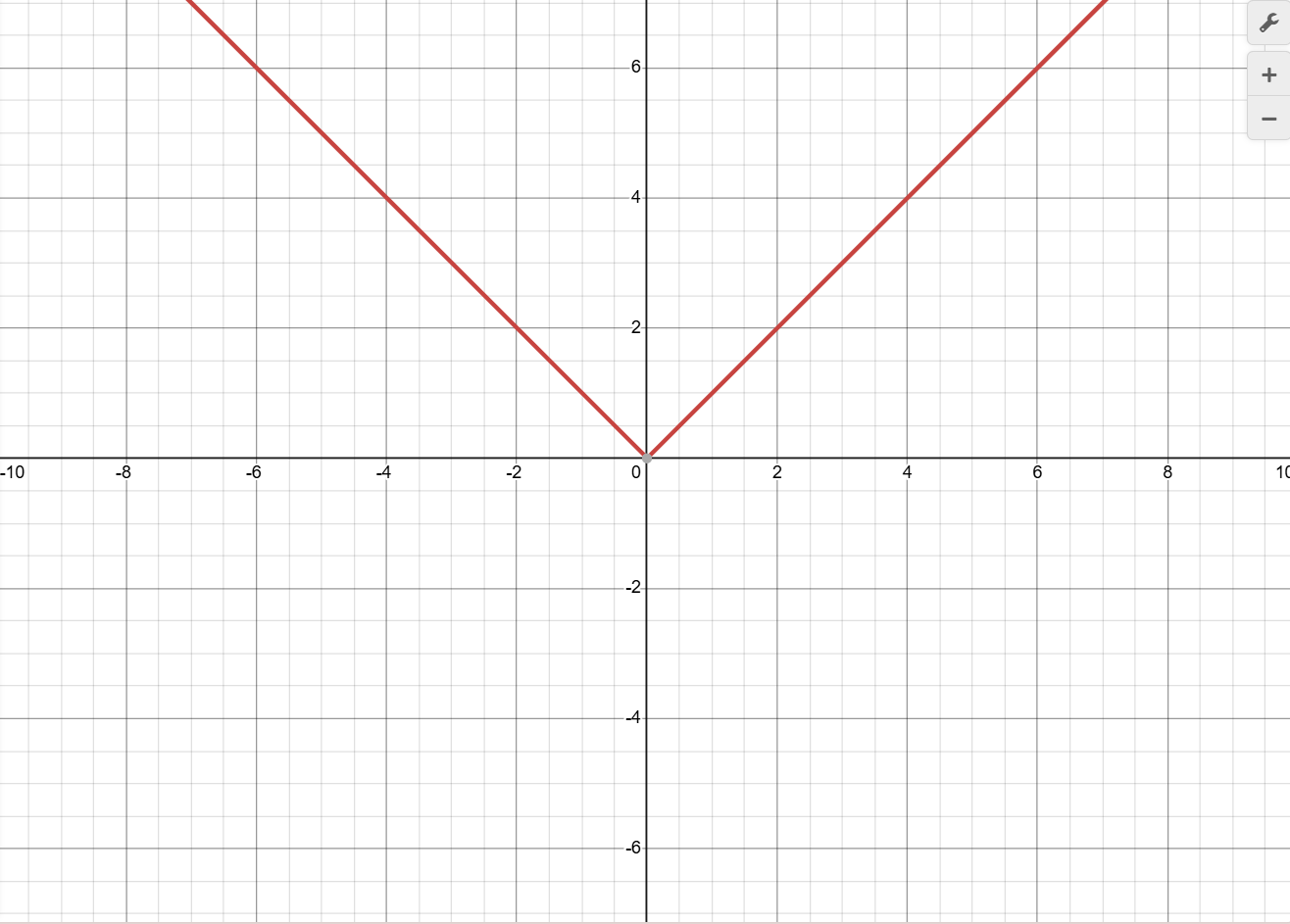
y=|x|

Domain (-∞, ∞)

Range [0, ∞)

(piecewise: x if x≥0; -x if x<0)

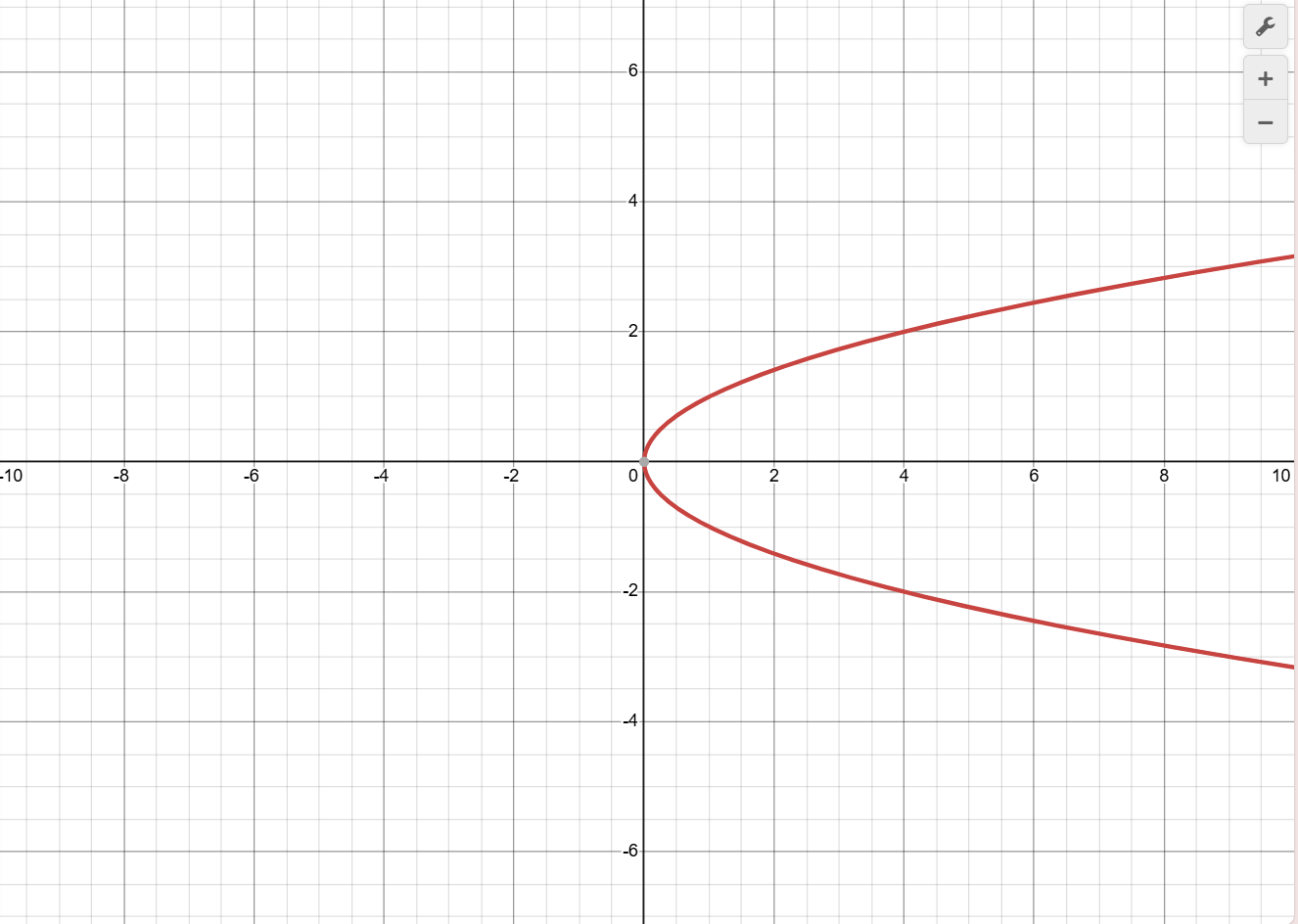
y²=x

Domain [0, ∞)

Range (-∞, ∞)

(not a function, doesn’t pass the vertical line test)

Point Slope Form

y-y₁=m(x-x₁)

Slope-Intercept Form (Linear Function)

y=mx+b

Quadratic Function

f(x)=ax²+bx+c

lim_(x→c)f(x) = L

“the limit, as x approaches c, of f(x) is (equal to) L” if the expression |f(x)-L| can be made arbitrarily small by taking x sufficiently close (but not equal to) c.

The Formal Definition of a Limit

If for any ε>0, there exists a δ>0 such that 0<|x-c|<δ, then the limit, as x approaches c, of functions f(x) is (equal to) L.

lim_(x→c)k

=k

lim_(x→c)x

=x

lim_(x→c^-)f(x)

exists and is value L for any ε>0, there exists e>0 such that whenever 0<c-x<δ, |f(x)-L|<ε

lim_(x→c⁺)f(x)

exists and is value L for any ε>0, there exists e>0 such that whenever 0<x-c<δ, |f(x)-L|<ε

Sum Law

lim_(x→c)(f(x)+ g(x)) = lim_(x→c)f(x) + lim_(x→c)g(x)

Constant Multiple Law

lim_(x→c)k*f(x) = k * lim_(x→c)f(x)

Product Law

lim_(x→c)f(x)g(x) = (lim_(x→c)f(x)) * (lim_(x→c)g(x))

Quotient Law

lim_(x→c)(f(x)/g(x)) = (lim_(x→c)f(x)) / (lim_(x→c)g(x))

Root Law

lim_(x→c)rt(n)(f(x)) = rt(n)(lim_(x→c)f(x))

Power Law

lim_(x→c)(f(x))^p/q = (lim_(x→c)f(x))^p/q

f is continuous at x=c if and only if

• f(c) is defined

• lim_(x→c)f(x) exists, and

• lim_(x→c)f(x) = f(c)

f(x) has a removable discontinuity if

lim_(x→c)f(x) exists but either lim_(x→c)f(x) ≠ f(c) or f(c) does not exist at all

Jump Discontinuity

lim_(x→c^-)f(x) ≠ lim_(x→c⁺)f(x), but both limits exist

Infinite Discontinuity

If one or both of the land- and right-hand limits of a function as x→c tends towards either ∞ or -∞

Left-Continuous

If lim_(x→c^-)f(x) = f(c), even though the fn may be discontinuous at x=c

Right-Continuous

If lim_(x→c⁺)f(x) = f(c), even though the fn may be discontinuous at x=c

Indeterminate Forms

• 0/0

• +∞/+∞

• ∞*0

• ∞-∞

• 0⁰

• 0^+-∞

• +∞⁰

The Squeeze Theorem

l(x)≤f(x)≤u(x)

If it is the case that lim_x→cl(x) = lim_x→cu(x) = L

then it must also be that lim_x→cf(x) = L

lim_{x→ -∞}e^x

=0

R(x) = p(x)/q(x) when the degree of p is less than the degree of q

There is a horizontal asymptote of y=0

R(x) = p(x)/q(x) when the degree of p is greater than the degree of q

There are no horizontal asymptotes

R(x) = p(x)/q(x) when the degree of p is equal to the degree of q

There is a horizontal asmyptote at y = (leading coefficient of p / leading coefficient of q)