Chapter 4: Other Graphs

Equations for other strange but interesting graphs.

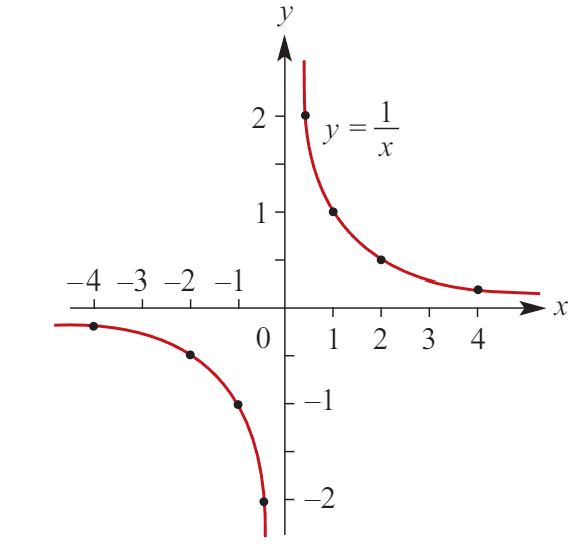
Hyperbolas

Equation: y=a/x-h + k

Dilation factor: a

Reflection: ± about the x-axis (if negative, 2/4 quadrant; if positive, 1/3 quadrant.)

Transformation: h units right and k units up

Asymptotes: x=h or y=k

Asympotes

Horizontal: As x→±∞, y→0^± (As x approaches (negative) infinity, y approaches 0 from positive/negative side).

Vertical: As x→0^±, y→±∞ (As y approaches (negative) infinity, x approaches 0 from positive/negative side).

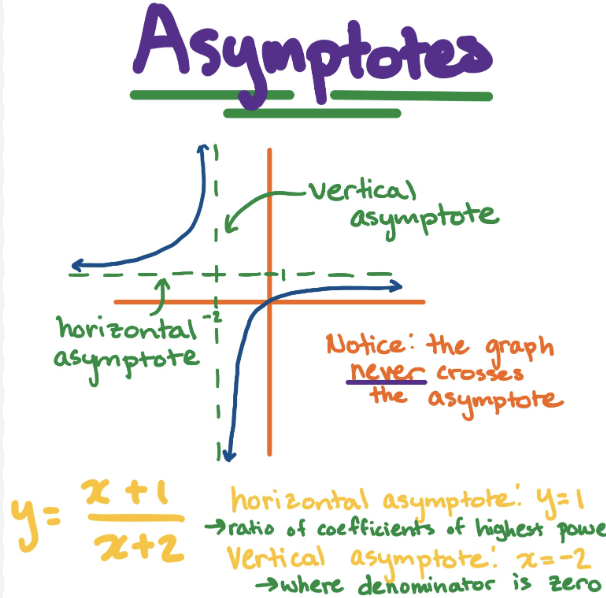
Truncus

Equation: y=a/(x-h)² + k

Dilation factor: a

Reflection: ± about the x-axis (1/2 quadrant when positive; ¾ quadrant when negative)

Transformation: h units right and k units up

Asymptotes at x=h or y=k

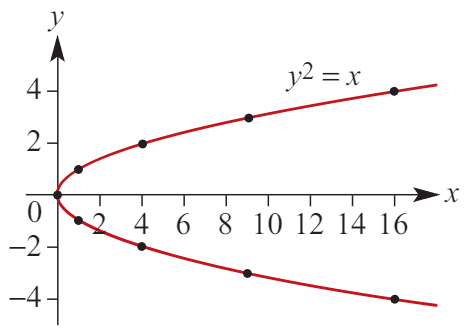
y² = x

A parabola like y=x² but plotted on y axis (rotated 90° clockwise).

Equation: (y-k)² = a(x-h) / (y-k)² = a(h-x) IF NEG

Dilation factor: a

Reflection: ± about the y axis (left/right)

Transformation: k units up and h units right

Turning Point: (h,k)

Axis of Symmetry: y=k

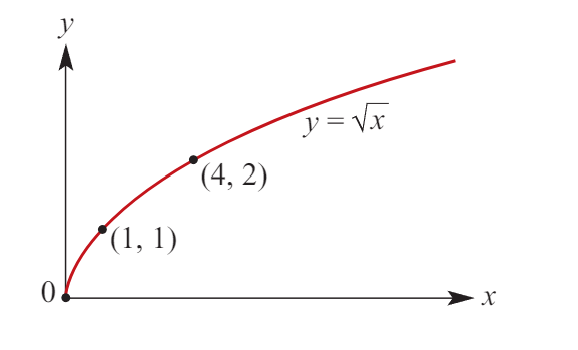
y = ñx

Equation: y = añ(x-h) + k

Dilation factor: a

Reflection: ± about the x-axis

Transformation: h units right, k units up

NOTE: Find the endpoint first. THIS WILL BE (h,k).

y=√-x: reflection in y-axis

y=-√x: reflection in x-axis

y=-√-x: reflection in both y and x-axis

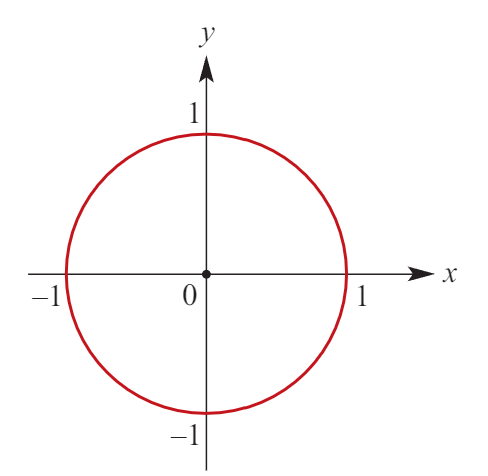
Circles

Equation: (x-h)² + (y-k)² = r² or x²+y²-2hx-2ky+c = 0

Dilation factor: r

Reflection: none

Transformation: h units right, k units up

Center: (h,k)

Radius: √r² = r

Semicircles

Equation: y = ± √r²-x² for top/bottom of the circle or x = ± √r²-y² for right/left of the circle

• For the top half of the semicircle:
  y = k + √(r² - (x - h)²)

• For the bottom half of the semicircle:
  y = k - √(r² - (x - h)²)

• For the right half of the semicircle:
  x = h + √(r² - (y - k)²)

• For the left half of the semicircle:
  x = h - √(r² - (y - k)²)

Dilation factor: none

Reflection: none

Transformation: none

Exam Tips

For ALL graphs mentioned, AT LEAST 2 POINTS are needed for the exam (if not x/y-int, plot RANDOM POINTS BY SUBSTITUTING RANDOM X/Y VALUES!!!)