CRYPTOGRAPHY

Cryptography

The study of mathematical techniques for securing digital information, systems, and distributed computations against adversarial attacks.

A private-key encryption scheme is specified by a message space M and three

algorithms:

ˆ Key Generation: KGen is a probabilistic algorithm that outputs a key k according to some

distribution

ˆ Encryption: Enc takes as input a key k and a message m, and outputs a ciphertext c

ˆ Decryption: Dec takes as input a key k and a ciphertext c, and outputs a message m

Kerckhoffs’ Principle

The cipher method must not be required to be secret, and it must be able to fall into the hands of the enemy without inconvenience.

which means key must be the o ly thing that remains secret.

Caesar’s cipher

Letters were shifted 3 places forward.

ROT-13 shift 13 places forward. type of caesar’s cipher.

Problems with Caesar’s Cipher

• cipher method is fixed;

• there is no key;

• fails to achieve Kerckhoffs principle

Shift Cipher

keyed variant of Caesar Cipher.

enc= shift k places forward'

dec= shift k places backward

is shift cipher secure? why or why not?

it is not restitant to brute force attacks

Sufficient Key-Space Principle

Any secure encryption scheme must have a key space that is sufficiently large to make an exhaustive-search attack infeasible

Mono alphabetic substituition

Key is an arbitary mapping of letters in the alphabet, ensuring each letter is consistently replaced by a specific letter throughout the message.

brute force attack is infeasibale due to the vast number of possible key combinations.

Is mono alphabetic substituition secure?

Attack possible using statistical properties of the English language

shift attack

compute Ij for all j and output the value k for

which Ik is closest to 0.065

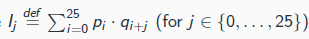
vigenere

Key is a string of letters,

brute force prob

statistical approach works

vignere attack

unknown key lentgh is ok

Kasiski’s method

• indentify repeated pattern of length 3 in the ciphertext

• Greatest common divisor of the distance between repeated sequences will yield the key length

  (or a multiple of it)

Index of coincedonce

security definitions’ two components:

1. A security guarantee (from view of the attacker an attacker’s goal that constitutes a break

of the scheme)

2. A threat model (describing what the adversary is capable of)

attackers’ goal

a ciphertext should leak no additional information about the underlying plaintext

threat models

• Ciphertext-only attack: The adversary just observes ciphertexts. This is the threat model we have been implicitly assuming thus far

• Known-plaintext attack: The adversary can learn some plaintext-ciphertext pairs and aims to deduce information of a plaintext underlying some other ciphertext

• Chosen-plaintext attack: The adversary can obtain plaintext-ciphertext pairs, as above, for plaintexts of its choice

• Chosen-ciphertext attack: The adversary is additionally able to obtain the decryption of ciphertexts of its choice

Principles of Modern Cryptography

1. definitions

2. precise assumptions

3. proofs of security

An encryption scheme is defined by?

three algorithms KGen, Enc, and Dec, as well as a specification of a message space M with |M| > 12, a (finite) key space K, and a ciphertext space C

perfect correctness?

for all k ∈ K and m ∈M, we have:

Pr[Dec(k, Enc(k,m)) = m] = 1

Perfect correctness implies that decryption is deterministic (without loss of generality), as Dec(k, c) must return the same output every time

Perfect Secrecy?

“Regardless of any prior information the attacker has about the plaintext, the ciphertext should leak no additional information about the plaintext”

For every m,m′ ∈M, and every c ∈ C, we have

Pr[Enc(k,m) = c] = Pr[Enc(k,m′) = c].

perfectly indistinguishable

if perf indist=> perf secret

One Time Pad

is perf secret

Limitations of the OTP?

ˆ key is as long as the message

ˆ only secure if the key is used once

perf secret encyrytion when?

Theorem 2.11

If (KGen, Enc, Dec) is a perfectly secret encryption scheme with message space M and key space K, then |K| ≥ |M|.

Shannon theorem

Message Integrity In block vs stream

Stream: flipping 1 bit results in whole message change

block: flipping one only affects that bit

MAC Defin?

A message authentication code (or MAC) consis of three probabilistic polynomial-time algorithms (KGen, Mac, Vrfy) such that:

1. The key-generation algorithm KGen takes as input the security parameter 1n and outputs a key k with |k| ≥ n.

2. The tag-generation algorithm Mac and a message m ∈ {0, 1}∗, and outputs a tag t. Since this algorithm may be randomized, we write this as t ← Mack (m).

3. The deterministic verification algorithm Vrfy takes as input a key k, a message m, and a tag t. It outputs a bit b, with b = 1 meaning valid and b = 0 meaning invalid. We write this as b := Vrfyk (m, t).

It is required that for every n, every key k output by KGen(1n), and every m ∈ {0, 1}∗, it holds that Vrfyk (m, Mack (m)) = 1.

If there is a function ℓ such that for every key k output by KGen(1n), algorithm Mack is only defined for messages m ∈ {0, 1}ℓ(n), then we call the scheme a fixed-length MAC for messages of length ℓ(n).

The adversarial indistinguishability experiment Mac-ForgeA,Π(n):

1. A key k is generated by running KGen(1n).

2. The adversary A is given input 1n and oracle access to Mack (·). The adversary eventually outputs (m, t). Let Q denote the set of all queries that A submitted to its oracle.

3. A succeeds if and only if

(1) Vrfy(k,m, t) = 1 and

(2) m /∈ Q.

In that case the output of the experiment is defined to be 1.

A message authentication code Π = (KGen, Mac, Vrfy) is existentially unforgeable under an adaptive chosen-message attack, or just secure, if for all probabilistic polynomial-time adversaries A there is a negligible function negl such that

Pr[Mac-ForgeA,Π(n) = 1] ≤ negl(n) .

Replay Attacks

an adversary sends again (“replays”) previously authenticated messages.

Prevention: use timestamps

Mac -s Forge

define the experiment Mac-sForgeA,Π similar to Mac-ForgeA,Π with the difference that Q stores pairs of oracle queries and responses and the final check is modified to (m, t) /∈ Q, for (m, t) the output of A

A message authentication code Π = (KGen, Mac, Vrfy) is strongly secure, if for all probabilistic polynomial-time adversaries A there is a negligible function negl such that

Pr[Mac-sForgeA,Π(n) = 1] ≤ negl(n) .

Macs Pseudorandom Fnc

Limitation of Construction 4.5: only messages of fixed-length can be handled, which is unacceptable for most applications

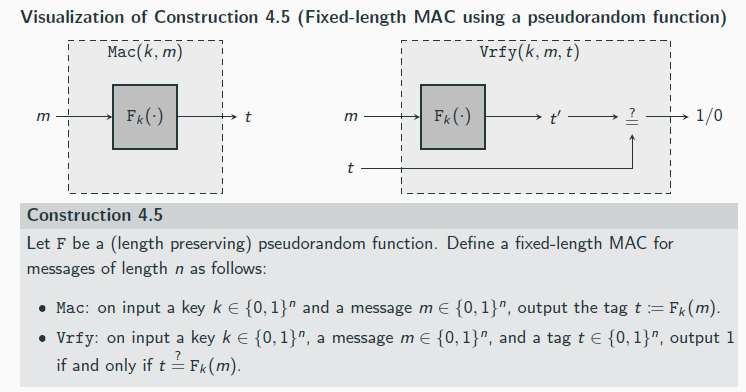
Secure Message Authentication Codes

add a random “message identifier” r in each block to prevent the“mix-and-match” attack

Let Π′ = (Mac′, Vrfy) be a fixed-length MAC for messages of length n. Define a MAC as

follows:

ˆ Mac: on input a key k ∈ {0, 1}n and a message m ∈ {0, 1}∗ of (nonzero) length ℓ < 2n/4, parse m as d blocks m1, . . . ,md , each of length n/4. (The final block is padded with 0s if necessary.) Choose a uniform message identifier r ∈ {0, 1}n/4.

For i = 1, . . . , d, compute ti ← Mac′ k (r ∥ ℓ ∥ i ∥ mi ), where i , ℓ are encoded as strings of length n/4. Output the tag t := ⟨r , t1, . . . , td ⟩.

ˆ Vrfy: on input a key k ∈ {0, 1}n, a message m ∈ {0, 1}∗ of nonzero length ℓ < 2n/4, and a tag t := ⟨r , t1, . . . , td′ ⟩, parse m as d blocks m1, . . . ,md , each of length n/4. (The final block is padded with 0s if necessary.) Output 1 if and only if d′ = d and Vrfy′ k (r ∥ ℓ ∥ i ∥ mi , ti ) = 1 for 1 ≤ i ≤ d.

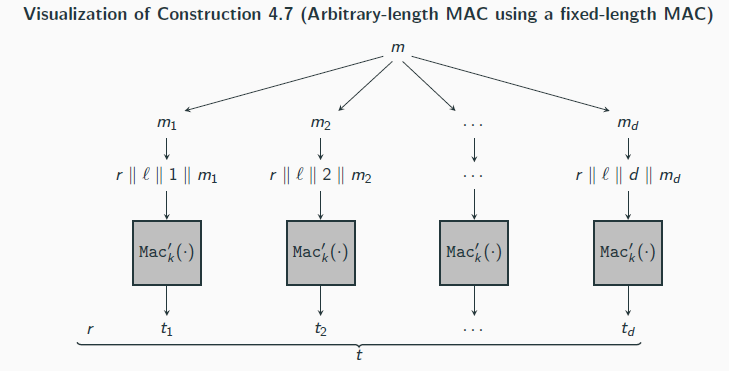
CBC-MAC

Let F be a pseudorandom function, and fix a length function ℓ(n) > 0. The basis CBC-MAC construction is as follows:

ˆ Mac: on input a key k ∈ {0, 1}n and a message m of length ℓ(n) · n, do the following (set ℓ = ℓ(n) in what follows):

1. Parse m and m = m1, . . . ,mℓ where each mi is of length n.

2. Set t0 := 0ⁿ. Then, for i = 1 to ℓ, set ti := F_k (ti−1 ⊕ mi )

Output tℓ as the tag.

ˆ Vrfy: on input a key k ∈ {0, 1}n, a message m, and a tag t, do: If m is not of length ℓ(n) · n then output 0. Otherwise, output 1 if and only if t ?= Mac_k (m).

Theorem 4.10

Let ℓ be a polynomial. If F is a pseudorandom function, then Construction 4.9 is a secure MAC for messages of length ℓ(n) · n.

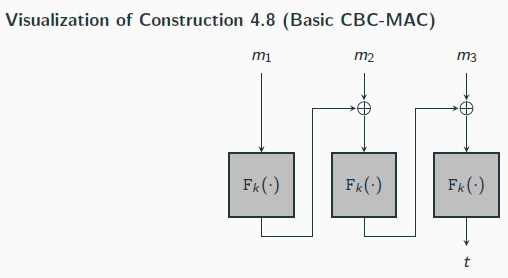
Basic CBC-MAC vs. Construction 4.5 and Construction 4.7

Compared to Construction 4.5, basic CBC-MAC can handle longer messages (though still fixed-length)

Compared to Construction 4.7, basic CBC-MAC is much more efficient: only d block-cipher evaluations for a message of length dn and a tag of length n (compared to 4d block cipher evaluations and tags of length more than 4dn)

CBC-MAC vs. CBC-mode encryption

Basic CBC-MAC is similar to the CBC mode of operation but there are crucial differences:

1. CBC-mode encryption uses a random IV, which is crucial for security. CBC-MAC uses no IV (can be viewed as constant IV iv = 0n), which is also crucial for security.

2. In CBC-mode encryption the intermediate values (ti in CBC-MAC) are output as part of the ciphertext. CBC-MAC only outputs the final value tℓ.

CCA Security

when is cca secure

CCA-security is a very strong requirement

→ Any encryption scheme where ciphertext can be “manipulated” in a controlled way cannot be CCA-secure

autheticatefd edncryption

achieves security and integrity

A private-key encryption scheme is an authenticated encryption (AE) scheme if it is CCA-secure and unforgeable.

auth encryp schem

authencry scheme

types of suth encry scheme

Let ΠE be a CPA-secure private-key encryption

scheme, and let ΠM be a strongly secure message

authentication code. Then Construction 5.6

(Encrypt-and-authenticate) is an authenticated

encryption scheme.

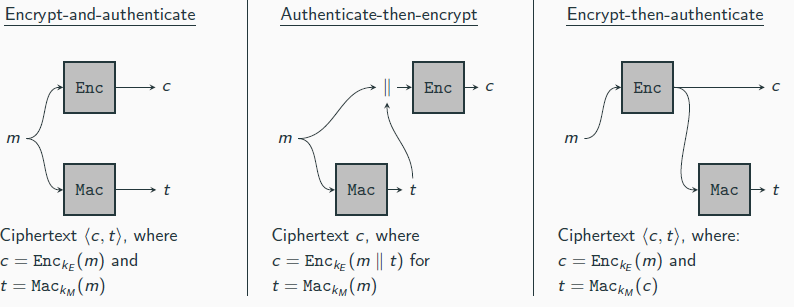
if no independent ,keys: he ciphertext reveals the message in the clear!

attack types

Using counters can mitigate the first three attacks; a directional bit can handle the fourth one4

“closed” system

“closed” systems: when there is a well-defined population of users who are willing to follow certain policies for distributing and storing keys

key distribution center (KDC)

large corporation where all pairs of employees must be able to communicate securely

We can assume that the employees trust some entity, e.g., the system administrator—at leastregarding work-related communication

This trusted party can act as a KDC:

ˆ whenever a new employee joins the corporation, it receives a key shared between the employee and the KDC

ˆ when an employee wants to communicate with another employee, it can request a (session) key from the KDC.

+ Each employee needs to store only one long-term key (the one shared with the KDC); session keys are short-term that can be erased after the session

+ For each new employee only that employee must set up a key with the KDC; no other employee needs to do anything

- The KDC is a high-value target: a successful attack on the KDC will result in a complete break of the system

-The KDC is a single point of failure: if the KDC is offline, secure communication is temporarily impossible.

Diffie and Hellman

proposed a protocol for Alice and Bob to securely exchange a key via a public but authenticated (an attacker cannot interfere with their communication)

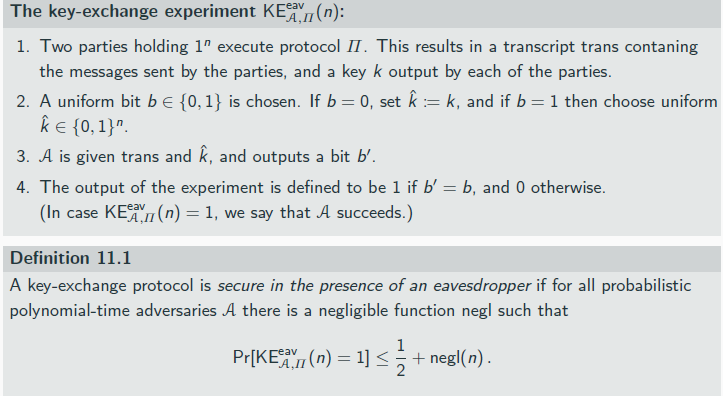
Diffie and Hellmanexchange protocol

Hardness of the CDH problem guarantees that it is hard to compute the entire key from thetranscript

→ also not sufficient to prove security

Definition 11.1 requires that the shared key gxy to be indistinguishable from uniform for any adversary given g, gx , gy (the transcript)

→ this is exactly the DDH problem

diifie hellman prob;lem

public-key cryptography

a party generates a pair of keys:

ˆ a public key pk that is widely disseminated, e.g., putting it on a website

ˆ a private key sk that is kept secret

public-key cryptography is strictly stronger than private-key cryptography

Private-key cryptography is much more efficient than public-key cryptography and should be used whenever the setting allows it.

publib key setting

Public-key encryption

ˆ everyone with the public key can encrypt

ˆ decryption is only possible with the private key

ˆ security holds even against adversaries that know the public key for encryption

Digital signature schemes

ˆ Analogue of message authentication codes in the asymmetric setting

ˆ using the private key, one can generate a signature of a message

ˆ the public key allows to verify a message-signature pair

ˆ digital signature schemes provide so-called non-repudiation (which MACs do not): one can present a message-signature pair by Alice to a judge who can verify that Alice indeed signed the message

diffie helman explain

Uniform group elements vs. uniform bit-strings

ˆ Alice and Bob can apply a key-derivation function to their shared secret gxy to obtain a bit-string that is indistinguishable from random to be used as a key for subsequent cryptographic applications

Active adversaries

ˆ only secure againsteavesdropping adversaries

ˆ It is completely insecure against man-in-the-middle attack

Diffie–Hellman key-exchange in practice

ˆ The basic protocol serves as a first demonstration of asymmetric techniques (and problemsfrom number theory) to solve the problem of key distribution

ˆ The protocol—with proper modifications to withstand also man-in-the-middle attacks—is widely used today

block cipher security

→ A block cipher is considered “secure” if the best known attack (without preprocessing) has time complexity roughly equivalent to a brute-fore search for the key

→ in the asymptotic setting this attack corresponds to a complexity of 2n/2 which is still exponential

ciphers should be concise, random-looking permutations

Hash function

Collisons

Second-preimage resistance vs Preimage resistance

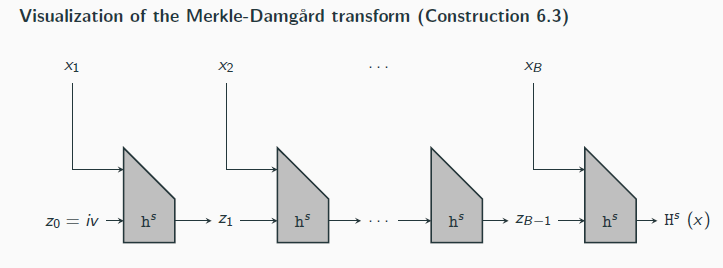
Merkle-Damg˚ard Transform

Merkle-Damg˚ard Transform visualization

If (KGen, h) is collision resistant, then so is (KGen, H) from Construction 6.3.

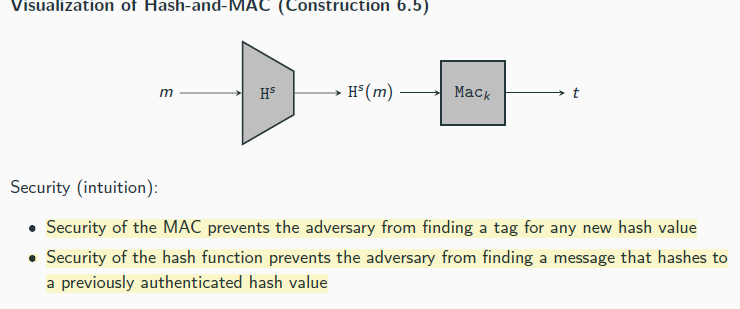
Hash and Mac

Let Π = (Mac, Vrfy) be a MAC for messages of length ℓ(n), and let H = (KGenH, H) be a hash function with output length ℓ(n). Construct a MAC Π′ = (KGen′, Mac′, Vrfy′) for arbitrary-length messages as follows:

ˆ KGen′: on input 1n, choose uniform k ∈ {0, 1}n and run KGenH(1n) to obtain s; output the key (k, s).

ˆ Mac′: on input a key (k, s) and a message m ∈ {0, 1}∗, output t ← Mack (Hs (m)).

ˆ Vrfy′: on input a key (k, s), a message m ∈ {0, 1}∗, and a tag t, output 1 if and only if : Vrfyk (Hs (m), t) ?=1.

If Π is a secure MAC for messages of length ℓ(n) and H is collision resistant, then Construction 6.5 is a secure MAC (for arbitrary-length messages).

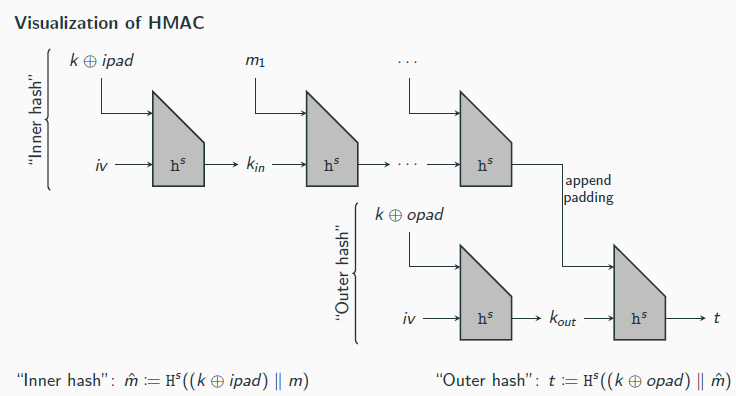
HMAC

Let (KGenH, H) be a hash function constructed by applying the Merkle-Damg˚ard transform to a compression function (KGenh, h) that takes inputs of length n + n′ > 2n + log n + 2 and generates outputs of length n. Fix distinct constants opad, ipad ∈ {0, 1}n′ . Define a MAC as follows:

ˆ KGen′: on input 1n run KGenH(1n) to obtain a key s. Also choose a uniform k ∈ {0, 1}n′.

Output the key (s, k).

ˆ Mac′: on input a key (s, k) and a message m ∈ {0, 1}∗, output

t := Hs ((k ⊕ opad) ∥ Hs ((k ⊕ ipad) ∥ m)) .

ˆ Vrfy′: on input a key (s, k), a message m ∈ {0, 1}∗, and a tag t, output 1 if and only if t ?= Hs ((k ⊕ opad) ∥ Hs ((k ⊕ ipad) ∥ m)).

“computational independence” of kin def = hs (iv ∥ (k ⊕ ipad)) and kout . Define

Gs (k) def = hs (iv ∥ (k ⊕ ipad)) ∥ hs (iv ∥ (k ⊕ opad)) = kin ∥ kout

Theorem 6.8

Assume Gs is a pseudorandom generator eΠ s is a secure fixed-length MAC for messages of length n′, and (KGenH, h) is collision resistant. Then HMAC is a secure MAC (for arbitrary-length messages).

Random Oracle Model

1. A scheme is designed and proven secure in the random-oracle model

→ security experiment is enhanced by a random oracle to which everyone (experiment itself, adversary, and reduction) have access to

2. To use the scheme in the real world (where we do not have random oracles), one instantiates RO with an appropriately designed cryptographic hash function H. This means that each time a party should query the random oracle on input x, the party instead computes H(x) on its own

The idea: if the hash function in the second step is “sufficiently good” at emulating a random oracle, the security proof from the first step will carry over to the real-world instantiation

Three properties of security proofs in the random-oracle model:

1. If x has not been queries to RO, then the value of RO(x) is uniform

2. If A queries x to RO, the reduction can see this query and learn x

→ this is called “extractability”

3. The reduction can set the value of RO(x) (i.e., the response to query x) to a value of its choice, as long as this value is correctly distributed, i.e., uniform

→ this is called “programmability”

Disadvantages:

ˆ There is no such thing as a public hash funcion that “is random”

ˆ There are known counterexamples

Advantages:

ˆ No example of a “natural” scheme secure in the random-oracle model being attacked in the real world

ˆ If an attack is found, simply replace the hash function

ˆ A proof in the random-oracle model is better than no proof at all

→ provides evidence that design principle is sound

digital signatures

a signature allows to verify that the intended update (instead of malware) was downloaded

Signature schemes are unilateral

Signature schemes allow everyone (subject to having the public key) to verify a signature

they offer non-repudiation

It is required that except with negligible probability over (pk, sk) output by KGen(1ⁿ), it holds that Vrfy_pk (m, Sign_sk (m)) = 1 for every (legal) message m.

If there is a function ℓ such that for every (pk, sk) output by KGen(1ⁿ) the message space is {0, 1}^ℓ(n), then we say that (KGen, Sign, Vrfy) is a signature scheme for messages of length ℓ(n).

Secure distribution of the public key may be difficult and expensive but it needs to be done only once; afterwards Alice can send an arbitrary number of messages that she signed

Furthermore, signature schemes itself are used to ensure the secure distribute other public keys

Security of signature schemes

A signature scheme Π = (KGen, Sign, Vrfy) is existentially unforgeable under an adaptive chosen-message attack, or just secure, if for all probabilistic polynomial-time adversaries A there is a negligible function negl such that:

Pr[Sig-ForgeA,Π(n) = 1] ≤ negl(n) .

signature schemes less effiecient when compared to MACs

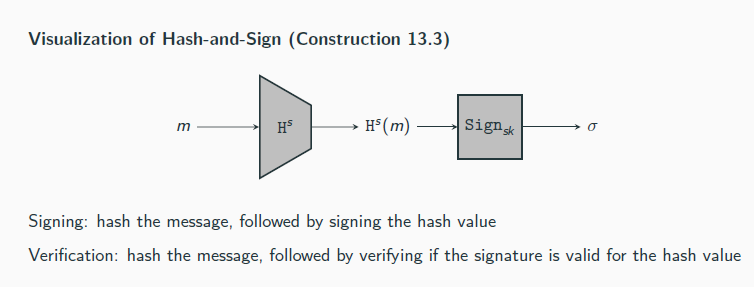
Hash and Sign

Let Π = (KGen, Sign, Vrfy) be a signature scheme for messages of length ℓ(n), and let H = (KGenH, H) be a hash function with output length ℓ(n). Construct a signature scheme Π′ = (KGen′, Sign′, Vrfy′) as follows:

ˆ KGen′: on input 1n, run KGen(1ⁿ) to obtain (pk, sk) and run KGen_H(1ⁿ) to obtain s; the public key is ⟨pk, s⟩ and the private key is ⟨sk, s⟩

ˆ Sign′: on input a private key ⟨sk, s⟩ and a message m ∈ {0, 1}∗, output σ ← Sign_sk (H^s (m)).

ˆ Vrfy′: on input a public key ⟨pk, s⟩, a message m ∈ {0, 1}∗, and a signature σ, output 1 if and only if Vrfy_pk (H^s (m), σ) ?= 1.

If Π is a secure signature scheme for messages of length ℓ(n) and H is collision resistant, then Construction 13.3 is a secure signature scheme (for arbitrary-length messages).

RSA Based signatures

sk = ⟨N, d⟩ and pk = ⟨N, e⟩

Construction 13.5 (Plain RSA Signature)

Let GenRSA be as before. Define a signature scheme as follows:

ˆ KGen: on input 1n run GenRSA(1n) to obtain (N, e, d). The public key is ⟨N, e⟩ and the private key is ⟨N, d⟩.

ˆ Sign: on input a private key sk = ⟨N, d⟩ and a message m ∈ Z∗_N, compute the signature σ := [m^d mod N] .

ˆ Vrfy: on input a public key pk = ⟨N, e⟩, a message m ∈ Z∗ N, and a signature σ ∈ Z∗_N, output 1 if and only if m ?= [σ^e mod N] .

Attacks against RSA

No-Message-Attack:

1. choose σ ∈ Z∗_N

2. compute m := [σ^e mod N]

3. output (m, σ)

by trying mutliple, uniform σ, the adversary can find a message m with a few bits set is a specific way

Forgery for arbitrary message m:

1. choose m1,m2 ∈ Z∗_N distinct from m such that m = m1 · m2 mod N

2. get signatures σ1 and σ2 for m1 and m2, respectively (→ two queries to oracle Sign)

3. output σ := [σ1 · σ2 mod N] as a signature of m

Verification: σ_e = (σ1 · σ2)_e = (m₁^d · m₂^d)^e = m₁^de· m₂^de= m1 · m2 = m mod N

→ obtaining signatures for m1 and m2 is not so hard in practice, making this a devastating attack!

→ generalization: having signatures on q messages M = {m1, . . . ,mq} allows to generate valid signatures for any combination of messages in M

RSA-FDH

transformation to the message before signing them

→ this yields RSA full-domain hash (RSA-FDH)

Let GenRSA be as before, and construct a signature scheme as follows:

ˆ KGen: on input 1ⁿ run GenRSA(1ⁿ) to obtain (N, e, d). The public key is ⟨N, e⟩ and the private key is ⟨N, d⟩. As part of key generation, a function H: {0, 1}∗ → Z∗_N is specified, but we leave this implicit.

ˆ Sign: on input a private key sk = ⟨N, d⟩ and a message m ∈ Z∗ _N, compute σ := [H(m)^d mod N] .

ˆ Vrfy: on input a public key pk = ⟨N, e⟩, a message m ∈ Z∗_N, and a signature σ ∈ Z∗_N,output 1 if and only if σ^e ?=[H(m) mod N] .

RSA-FDH to be secure?

1. H has to be hard to invert

→ absence of this enables the first attack discussed above

2. H must not admit “multiplicative relations”, meaning it should be hard to find m, m1, m2 with H(m) = H(m1) · H(m2) mod N

→ absence of this enables the second attack discussed above

3. H must be collision resistant

→ absence of this allows for forgery attacks as colliding messages have the same signatures

If the RSA problem is hard relative to GenRSA and H is modeled as a random oracle, then

Construction 13.6 is secure.

public-key infrastructure (PKI)

digital certificates→ signatures binding a public key to an identity

Simplest PKI: a single certification authority (CA) who everyone trusts

→ not a single person but a company

Multiple certification authorities

A single CA is simple and appealing, but . . .

ˆ . . . it is unlikely that everyone trusts this CA

→ does not have to mean that the CA is corrupt; maybe Alice simply finds the CA’s verification process to be insufficient

ˆ . . . this CA is a single point of failures

Instead, Bob can obtain multiple certificates (from different CAs) and Alice can decide based on whether there is a certificate from any CA that she trusts

Delegation and certificate chains

Certification chains can alleviate the burden of a single CA

The idea of certificate chains can be used to build a PKI via a hierarchical structure .

A CA-based PKI can consist of a “root” CA and n “second-level” CAs CA1, . . . , CAn

→ the root CA can issue certicates for the second-level CAs

→ the second-level CAs can then issue certificates for users

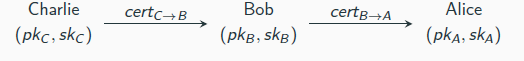
Invalidating Certificates

Certificates should not be valid indefinitely

→ employees might leave the company after which they should no longer receive encrypted communication from others

→ private keys might be stolen

1. EXPIRATION: A certificate issued by Charlie for Bob will be of the form certC→B _def = Sign_skC (“Bob’s key is pkB ”, date) ,

   where date is some date in the future at which points the certificate becomes invalid

   Alice would now need to check both the validity of the signature and that the exp:

2. REVOCATION: A certificate will contain a serial number ###, i.e., it will be of the form

   certC→B_def = Sign_skC (“Bob’s key is pkB ”, ###) ,

   where ### is a unique serial number

   To revoke a certificate, the CA can sign a so-called certificate revocation list (CRL) which contains the serial numbers of all revoked certificates, which are published on a regular basis,

   say, daily

   Alice would now need to check both the validity of the signature and that the serial number does not appear on the most recent CRL of the CA

Transport Layer Security (TLS)

protocol is used each time you visit a website using http TLS . . .

TLS protocol allows a client (e.g., a web browser) and a server (e.g., a website) to agree on a set of shared keys, followed by using them for subsequent communication

TLS protocol consists of two components:

1. a handshake protocol

2. a record-layer protocol

allows for mutual authentication

→ primary usage: only the server authenticates to the client (the reason is that typically only the servers have certificates)

→ client-to-server authentication can be done afterwards

Handshake protocol

Client C holds a set of CAs’ public keys {pk1, . . . , pkn}; the server S holds a key-pair (pkS , skS ) of a signature scheme and a certificate certi→S on pkS (a certificate issued by one of the CAs)

Security (intuition):

ˆ Certificate certi→S allows the client to be sure that it received the correct public key from the intended server

ˆ Signature σtrans convinces that the client is comunicating with the server

→ the value NC chosen by the client ensures that the signed message (the transcript) has high entropy to protect against replay attacks

ˆ Signature σtrans also guarantees that the messages from the Diffie-Hellman key-exchange were not modified in transit

→ this excludes man-in-the-middle attacks

ˆ Security of the Diffie–Hellman protocol ensures that an observing adversary learns nothing about the exchanged keys k′S , k′C , kS , kC

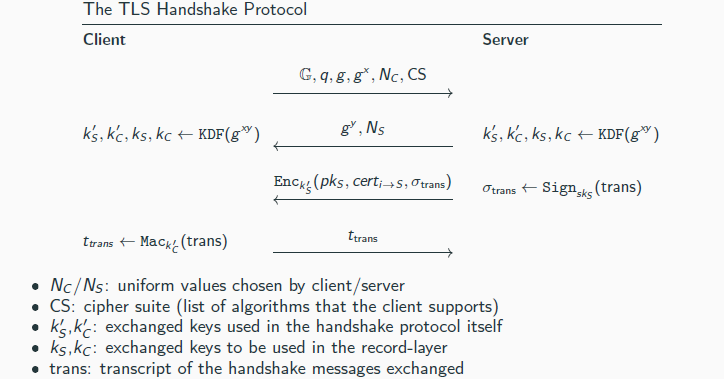
The record layer-protocol

Having keys kC and kS from the handshake protocol, client C and server S use those for an authenticated encryption to encrypt and authenticate their subsequent communication:

ˆ Key kC is used for messages from C to S

ˆ Key kS is used for messages from S to C

ˆ Sequence numbers are used to prevent replay attacks

The confusion-diffusion paradigm

Given x ∈ {0, 1}128, parse it as 16 bytes x1 · · · x16 and set

Fk (x) = f1(x1) ∥ · · · ∥ f16(x16)

The round functions {fi} introduce confusion into F

Clearly, F is not pseudorandom

→ if x and x′ differ only in the first byte, then Fk (x) and Fk (x′) only differ in the first byte

A diffusion step is added that “mixes” the output bits using a mixing permutation

→ idea: local changes should spread through the entire block

The confusion/diffusion steps (together called a round) are repeated multiple times

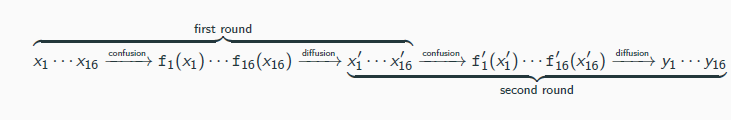
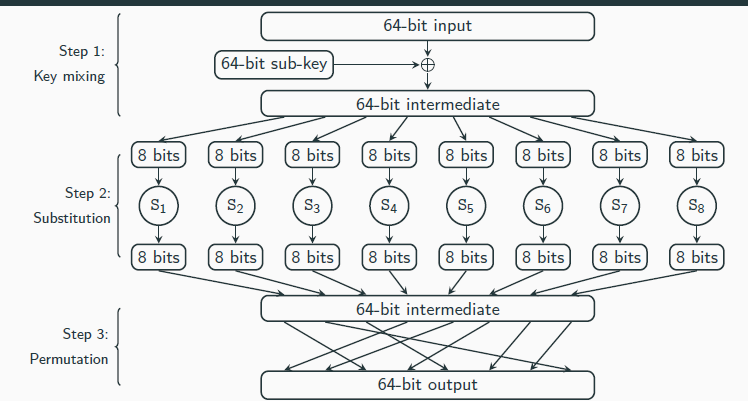
SPN (Substitutrion Permutation Network)

Consider an example using 64-bit block length with 8-bit S-boxes S1, . . . , S8

Evaluating the cipher proceeds in a series of rounds, each of which consists of the following sequence of operations to the input x of that round:

1. Key mixing: Set x := x ⊕ k, where k is the current-round sub-key;

2. Substitution: Set x := S1(x1) ∥ · · · ∥ S8(x8), where xi is the ith byte of x;

3. Permutation: Permute the bits of x to obtain the output of the round.

Input to the cipher is the input to the first round

Output of a round is the input to the next round

After the final round, a final key-mixing step is applied and the result is the output of the cipher

Each round uses different sub-keys (or round keys)

The key of the block cipher is often called the master key

Round keys are derived from the master key according to a key schedule

The key schedule is often simple, e.g., use different subsets of the bits of the master key

→ more complex key schedules can also be defined

An r round SPN has:

ˆ r rounds of key mixing, S-box substitutions, and applications of a mixing permutations

ˆ 1 (final) key mixing step

This means that r + 1 sub-keys

inverting SPN

An SPN is invertible (given the key):

ˆ If each round is invertible, one can invert the whole SPN round-by-round

ˆ Inverting each round:

ˆ (Step 3) Mixing permutation can easily be inverted as it just shuffles the bits

ˆ (Step 2) S-boxes are permutations, hence also invertible

ˆ (Step 1) XORing the correct sub-key then yields the original input

avalanche effect in spn

small changes in the input must “affect” every bit of the output

1. The S-boxes are designed so that changing a single bit of the input to an S-box changes at least two bits in the output of the S-box

2. The mixing permutations are designed so that the bits output by any given S-box affect the input to multiple S-boxes in the next round

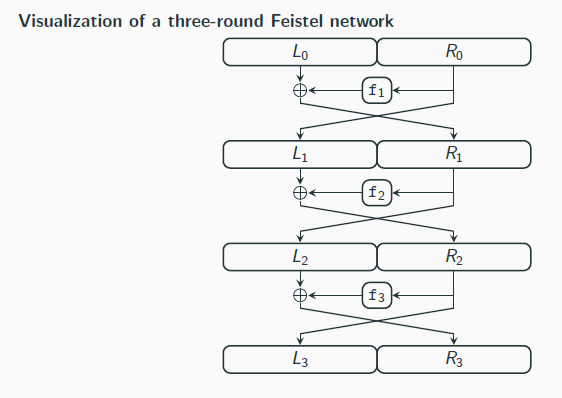
Feistel Networks

A substitution permutation networks constructs a permutation from invertible components

A Feistel network constructs a permutation from non-invertible components

In a (balanced) Feistel network with ℓ-bit block length, the ith round function ^fi takes as input a sub-key ki and an ℓ/2-bit input and outputs an ℓ/2-bit output

When some master key k, which defines sub-keys ki for each round, is chosen, define fi : {0, 1}ℓ/2 → {0, 1}ℓ/2 via fi (R) def = ^fi (ki , R)

The ith round of a Feistel network works as follows:

1. the ℓ-bit input is split into two halves denoted by Li−1 and Ri−1

2. the output is (Li , Ri ), where Li := Ri−1 and Ri := Li−1 ⊕ fi (Ri−1)

is invertible regardless of the {fi}

ˆ If each round is invertible, one can invert the whole Feistel network

ˆ Given (Li , Ri ) (output of the ith round):

1. Set Ri−1 := Li

2. Compute Li−1 := Ri ⊕ fi (Ri−1)

3. Output (Li−1, Ri−1)

→ note that we only to evaluate fi in the forward direction

AES

AES comes in three variants AES-128, AES-192, and AES-256 that use 128-, 192-, and 256-bit keys, respectively

The block length for all variants is ℓ = 128

The design of AES is essentially a substitution-permutation network:

ˆ AES operates on a state that is represented as a 4-by-4 array of bytes (in total 128 bits)

ˆ The state is modified through a series of rounds, each consisting of 4 stages:

AddRoundKey | {z } SPN: Key mixing , SubBytes | {z } SPN: Substituion, |ShiftRows, a{nzd MixColumns} SPN: Permutation

ˆ The initial state is set to be the input of the block cipher

The number of rounds depend on the key length:

ˆ AES-128: 10 rounds

ˆ AES-192: 12 rounds

ˆ AES-256: 14 rounds

Davies-Meyer

the ideal-cipher model implies . . .

ˆ . . . the absence of related-key attacks

→ F(k, ·) and F(k′, ·) must behave independently even if k and k′ differ only in a single bit

ˆ . . . that there are no “weak keys”, say, k = 0n for which F(k, ·) is easy to distinguish from random

Theorem 7.5

If F is modeled as an ideal cipher, then any attacker making q queries to F or F−1 can find a collision in the Davies–Meyer construction with probability at most q2/2ℓ.

SHA-2 is currently recommended for collision-resistant hashing

Keccak

Fix π : {0, 1}ℓ → {0, 1}ℓ and constantes r , c, v, and λ > 1. Hash function H, on input ˆm ∈ {0, 1}∗, does:

(Padding) Append a 1 to ˆ m, followed by enough zeros so that the length of

the resulting string is a multiple of r . Parse the resulting string as

the sequence of r -bit blocks m1,. . . ,mt .

(Absorbing phase) Set y0 := 0ℓ. Then for i = 1, . . . , t do:

ˆ xi := yi−1 ⊕ (mi ∥ 0c ).

ˆ yi := π(xi ).

(Squeezing phase) Set y1∗ := yt , and let h1 be the first v bits of y∗1

Then for i = 1, . . . , λ do:

ˆ y∗i := π(y∗i−1).

ˆ Let hi be the first v bits of y∗ i .

(Output) Output h1 ∥ · · · ∥ hλ.

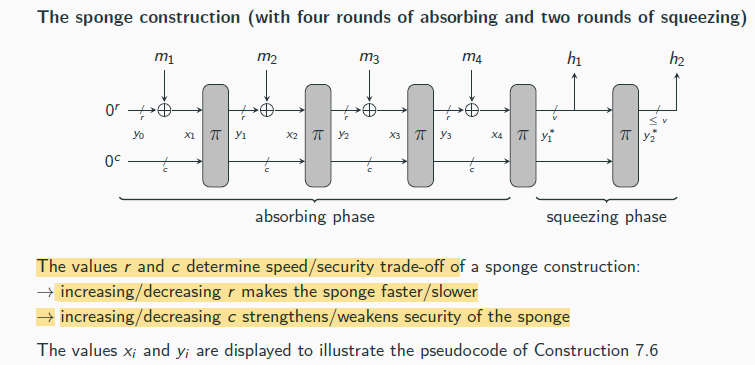
keccakk prob

Comparison to Private-Key Encryption

1. Secrecy of keys:

ˆ Private-key encryption requires secrecy of the key k

ˆ Public-key encryption requires secrecy only for the secret key sk—not the public key pk

2. Usage of keys:

ˆ Private-key encryption schemes use the same key for both encryption and decryption

ˆ Public-key encryption schemes use different keys for encryption and decryption → public-key encryption schemes allow only unilateral communication:

Main disadvantage of public-key encryption: it is roughly 2–3 orders of magnitude slower than private-key encryption

secure key distribtuion, i.e., that the sender receives a legitimate copy of the receiver’s public key

Public Encryoption scheme

It is required that, except with negligible probability over the randomness of KGen and Enc, we have Decsk (Encpk (m)) = m for any message m ∈Mpk .

The eavesdropping indistinguishability experiment

The eavesdropping indistinguishability experiment PubK^eav _A,Π(n):

1. KGen(1ⁿ) is run to obtain keys (pk, sk).

2. Adversary A is given pk, and outputs a pair of equal-length messages m0,m1 ∈Mpk .

3. A uniform bit b ∈ {0, 1} is chosen, and then a ciphertext c ← Enc_pk (mb) is computed and given to A. We call c the challenge ciphertext.

4. A outputs a bit b′. The output of the experiment is 1 if b′ = b, and 0 otherwise. If b′ = b we say that A succeeds.

having access to the public key essentially grants access to an encryption oracle for free → having pk, A can simply compute Encpk (m) for arbitrary m

If a public-key encryption scheme has indistinguishable encryptions in the presence of an eavesdropper, it is CPA-secure.

perfectly secret public-key encryption is impossible

No deterministic public-key encryption scheme is CPA-secure.

Multiple encryptions

when a key (in this case a public key pk) is used multiple times

Let LRpk,b(·, ·) be a “left-or-right” oracle, which on input two equal-length messages m0 and m1 computes and returns the ciphertext c ← Encpk (mb)

The LR-oracle experiment PubKLR-cpa A,Π (n):

1. KGen(1n) is run to obtain keys (pk, sk).

2. A uniform bit b ∈ {0, 1} is chosen.

3. The adversary A is given input pk and oracle access to LRpk,b(·, ·).

4. The adversary A outputs a bit b′.

5. The output of the experiment is defined to be 1 if b′ = b, and 0 otherwise. If

PubKLR-cpa A,Π (n) = 1, we say that A succeeds.

CCA security

1. A might send a modified ciphertext c′ to R on behalf of S

→ in case of encrypted email, A might construct an encrypted email c′ and forge the “From” field to make it look like it originates from S

→ subsequent behavior of R might reveal some information about m′ which in turn might reveal something about the original message m

2. A might send a modified ciphertext c′ to R in its own name

→ A might learn the entire decryption m′ of c′ if R responds directly to A (think of R responding to the email quoting the initial message)

The second class of attacks is specific to public-key encryption schemes

The CCA indistinguishability experiment PubKcca A,Π(n):

1. KGen(1n) is run to obtain keys (pk, sk).

2. Adversary A is given pk and access to a decryption oracle Decsk (·). It outputs a pair of messages m0,m1 ∈Mpk of the same length.

3. A uniform bit b ∈ {0, 1} is chosen, and then a ciphertext c ← Encpk (mb) is computed and given to A.

4. A continues to interact with the decryption oracle, but may no request a decryption of c itself. Finally, A outputs a bit b′.

5. The output of the experiment is 1 if b′ = b, and 0 otherwise.

KEM DEM Paradigm

A key-encapsulation mechanism (KEM) is a tuple of probabilistic polynomial-time algorithms (KGen, Encaps, Decaps) such that:

1. The key-generation algorithm KGen takes as input the security parameter 1n and outputs a public-/private-key pair (pk, sk). We assume pk and sk each has length at least n, andthat n can be determined from pk.

2. The encapsulation algorithm Encaps takes as input a public key pk (which implicitly defined n). It outputs a ciphertext c and a key k ∈ {0, 1}ℓ(n), where ℓ is the key length. We write this as (c, k) ← Encapspk(1n).

3. The deterministic decapsulation algorithm Decaps takes as input a private key sk and a ciphertext c, and outputs a key k or a special symbol ⊥ denoting failure. We write this as k := Decapssk (c).

It is required that with all but negligible probability over the randomenss of KGen and Encaps, if Encapspk(1n) outputs (c, k) then Decapssk (c) outputs k.

Let Π = (KGen, Encaps, Decaps) be a KEM with key length n, and let

Π′ = (KGen′, Enc′, Dec′) be a private-key encryption scheme. Construct a public-key encryption scheme Πhy = (KGenhy , Enchy , Dechy ) as follows:

ˆ KGenhy : on input 1n run KGen(1n) and use the public and private key (pk, sk) that are output.

ˆ Enchy : on input a public key pk and a message m ∈ {0, 1}∗ do:

1. Compute (c, k) ← Encapspk(1n).

2. Compute c′ ← Enc′ k (m).

3. Output the ciphertext ⟨c, c′⟩.

ˆ Dechy : on input a private key sk and a ciphertext ⟨c, c′⟩ do:

1. Compute k := Decapssk (c).

2. Output the message m := Dec′ k (c′).

ˆ If Π is a CPA-secure KEM and the private-key encryption scheme Π′ is EAV-secure, the Πhy is CPA-secure public-key encryption scheme

ˆ If Π is a CCA-secure KEM and Π′ is a CCA-secure private-key encryption scheme, the Πhy is CCA-secure public-key encryption scheme

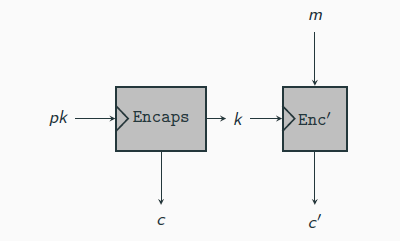
ElGamal

Lemma 12.15

Let G be a finite group, and let m ∈ G be arbitrary. Then choosing uniform k ∈ G and setting c := k · m results in a uniformly distributed c ∈ G. Put differently, for any ˆc ∈ G, we have

Pr[k · m = ˆc] =1/|G|

where the probability is taken over uniform choice of k ∈ G.

this effectively gives a perfectly secret private-key encryption scheme:

ˆ The key k is a uniform element k ∈ G

ˆ To encrypt m, Alice computes c := k · m

ˆ To decrypt c, Bob computes m := c/k

the one-time pad is an instantion of this, where G = {0, 1}ℓ and the group operation is bit-wise XOR

If the DDH problem is hard relative to G, then the ElGamal encryption scheme is CPA-secure.

Plain RSA Encryption

that one cannot compute the private key from the public key dure to hardness of factoring

Plain RSA is deterministic, hence it cannot be CPA-secure

Paded RSA Encryption

Let GenRSA be as before, and let ℓ be a function with ℓ(n) < 2n. Define a public-keyencryption scheme as follows:

ˆ KGen: on input 1n run GenRSA(1n) to obtain N, e, and d. The public key is ⟨N, e⟩ and the private key is ⟨N, d⟩. The message space is G.

ˆ Enc: on input a public key pk = ⟨N, e⟩ and a message m ∈ {0, 1}|N|−ℓ(n)−1, choose a uniform string r ∈ {0, 1}ℓ(n) and interpret ˆ m := r ∥ m as an element Z∗N. Output the ciphertext c := [ ˆ me mod N] .

ˆ Dec: on input a private key sk = ⟨N, d⟩ and a ciphertext c ∈ Z∗ N, compute ˆ m := [cd mod N] , and output the |N| − ℓ(n) − 1 least-significant bits of ˆ m.

→ security clearly depends on ℓ

One can perform a brute-force attack by encrypting a message under all possible random padding values

→ a too short ℓ (more precisely, ℓ(n) = O(log n)) makes the scheme insecure

for CCA attacvk on RSA u can recover message

OAEP

Let GenRSA and ℓ, k be as before. Let G : {0, 1}k → {0, 1}ℓ+k and H : {0, 1}ℓ+k → {0, 1}k be two functions. Construct a public-key encryption scheme as follows:

ˆ KGen: on input 1n, run GenRSA(1n) to obtain (N, e, d). The public key is ⟨N, e⟩ and the private key is ⟨N, d⟩.

ˆ Enc: on input a public key ⟨N, e⟩ and a message m ∈ {0, 1}ℓ, set m′ := m ∥ 0k andchoose a uniform r ∈ {0, 1}k . Then compute t := m′ ⊕ G(r ), s := r ⊕ H(t) and set ˆ m := s ∥ t. Output the ciphertext c := [ ˆ me mod N].

ˆ Dec: on input a private key ⟨N, d⟩ and a ciphertext c ∈ Z∗N, compute ˆ m := [cd mod N]. If∥ ˆ m∥ > ℓ+2k, output ⊥. Otherwise, parse ˆ m as s ∥ t with s ∈ {0, 1}k and t ∈ {0, 1}k+ℓ.5 Compute r := H(t) ⊕ s and m′ := G(r ) ⊕ t. If the k least-significant bits of m′ are not all 0, output ⊥. Otherwise, output the ℓ most-significant bits of m′.

Primes and divisilbilty

a | b if there exists c ∈ Z such that ac = b and a ∤ b if no such c exists

If a | b and a is positive: a is a divisor of b; If additionally a /∈ {1, b}, a is a nontrivial divisor or a factor of b

A positive p > 1 is prime if it has no factors

non-prime no.s >1 are composites

Let a be an integer and let b be a positive integer. Then there exist unique integers q, r for which a = qb + r and 0 ≤ r < b.

The greatest common divisor of integers a and b, denotes by gcd(a, b), is the largest integer c such that c | a and c | b

→ if p is prime then gcd(a, p) is either 1 or p

→ if gcd(a, b) = 1 we say that a and b are relatively prime

Let a, b be positive integers. Then there exists integers X,Y such that Xa + Yb = gcd(a, b). Furthermore, gcd(a, b) is the smallest positive integer that can be expressed this way

If a | N, b | N, and gcd(a, b) = 1, then ab | N.

If c | ab and gcd(a, c) = 1, then c | b. Thus, if p is prime and p | ab then either p | a or p | b.

Mofular arithmethic

By Proposition 9.1, there exist q, r such that a = qN + r with 0 ≤ r < N;m we define [a mod N] to be this r

Mapping a to [a mod N] is called reduction modulo N

We say that a and b are congruent modulo N (written as a = b mod N), if

[a mod N] = [b mod N]

\→ Note that a = b mod N if and only if N | (a − b)

Group

m = |G|, the order of the group. Then for any element g ∈ G, itnholds that gm =1

weak factor

For any n > 1, the fraction of n-bit integers that are prime is at least 1

3n .

factoring

rsa