Physics 114 Exam 4

Final Midterm for Physics

What do you mean by net force can be 0 but the object can still move?

The object can “rotate” if the net torque is not 0, meaning the object is not in static equilibrium. The angle at which the force acts can influence if the object will rotate about its pivot point.

What is the best place to apply a force? Like imagine on a door…

Perpendicular to the doors surface

Formula for Torque

T_q = r * F_{perpendicular}

• The force (in newtons) has to be the force that is perpendicular to the radial line.

A straight line from a pivot point is drawn out and a force is applied to it at an angle near one of its ends. What component/s of the force contribute to a torque?

Only the component that is PERPENDICULAR to the radial line r (the line drawn) will contribute to the torque.

What is a radial line?

The radial line is the distance from the pivot point to the point where the force is applied.

What is torque?

Torque is the ability of a force to rotate an object.

If a force goes clockwise around the pivot point, torque is…

Negative

If a force goes counterclockwise around the pivot point, torque is…

Positive

What are the conditions of static equilibrium?

Net force has to be 0…

Net torque has to be 0…

Describe how the center of mass would shift if a heavy object rested at the end of your pole balanced on a point…

The center of mass does NOT change!

• If other objects rest on or hang off an object, the objects center of mass does not change.

• The center of mass is a property of the object.

If force is applied AT the axis of rotation, how do you find the magnitude of that torque?

You don’t! It is 0!

• The force applied to the axis of rotation, at the axis of rotation, the torque is negligible because it will cause no torque.

• Forces applied at the axis of rotation cause no rotation so they cause no torque.

The total energy of a system is the same until…

Energy is transferred in or out of it via WORK.

• The total energy of a system can change if either W or Q are nonzero.

What is work?

Work (w) is the transfer of energy due to a force that pushes or pulls on the system.

What are the x and y components of the graph of which the area under the curve is the total work?

The y-axis is the force that is parallel to the direction the object moves…

The x-axis is the distance over which the object moves…

To get the work you find the area under this graph…

When given a graph of force vs distance (force parallel to the distance) what can you find?

The work done by this force is the area under the curve.

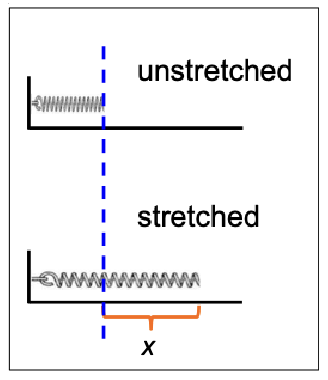
What will a graph of the MAGNITUDE of the spring force S versus x look like?

As distance (x) increases, the magnitude of spring force increases proportionally…so you should see a slope up in a straight line.

• NOTE this says MAGNITUDE meaning just the amount, so it will actually be a negative force that is getting more negative, but magnitude makes it positive.

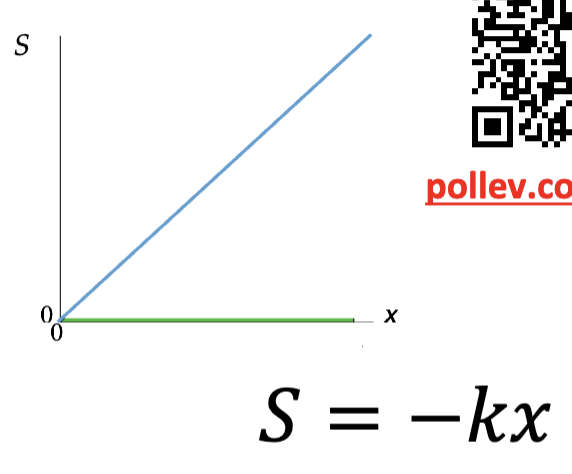
When given this graph of the spring force vs distance traveled, how might you calculate the total work done by this force?

• You know you need to find the area under the curve to get the work done by that force.

• So you multiply S by x then divide by 2…so 0.5*S*x

• S is actually equal to -kx, so you can plug it in and get…

• -0.5kx²

To find the work done by a force you multiply the component of the force that is (?) to the direction of displacement?

Parallel

• You multiply your force by the force that is parallel to the displacement.

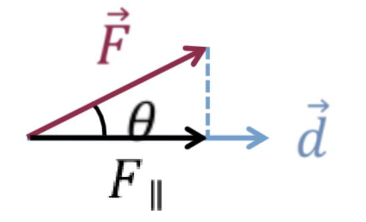
How might you find the work done by the force F acting on an object with a displacement d?

You would multiply the component of the F force that is parallel to the displacement.

Fcos() * d

• cosine of your angle gives you the component of the force that is parallel to the d!

• Multiply that force by the d to get the work performed by that force.

Is work a scalar or a vector?

Work is scalar.

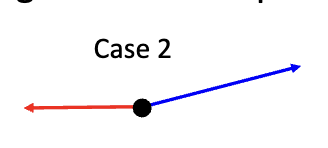
If the red line is the displacement and the angle between the red and the blue is 150º, how would you calculate the work done by force F (in blue)…

-Fcos(30º) = W

• You have to find the parallel force to the red displacement line (that is the x component of the blue line).

• You know this work will be negative because it is going in the opposite was as the displacement, so it will be slowing the displacement down.

A force that does positive work on an object tries to make the object?

Speed up!

• The work will be going in the direction of the displacement.

A force that does negative work on an object tries to make the object?

Slow down!

• The work will be going in the opposite direction of the displacement.

A force that does zero work on an object tries to make the object?

Move at a constant speed!

• It will be doing nothing to the object, similar to if acceleration is 0.

Simple equation for net work…

The sum of all the works done by all forces acting on an object.

any force that acts perpendicular to the displacement exerts a work force of…

0!

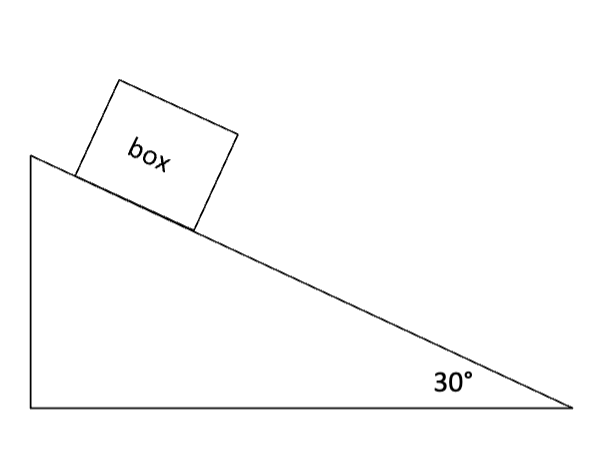
What forces are acting on this object? What is the work of each of these forces? What is the net work? (displacement is d)

u_k=0.1

d = 2

mass = 3.0kg

• Friction (up ramp), Weight x-comp (down ramp), Normal force (perpendicular to ramp)

• Normal Force: Work = 0

• Friction: Work = negative = u_kmgcos(30)*displacement

• Weight: Work = + = mgsin(30)*displacement

  • Add all the work up and get 24.3

An object m moving at speed v has a kinetic energy equal to…

K = 0.5mv²

What is the simplified work-kinetic energy theorum?

W_net,ext = ∆K

• The net work of the system is equal to the change in kinetic energy.

What would the formula for change in kinetic energy be? ∆K

Kinetic energy = 0.5mv²

So…

∆K = 0.5mv_f² - 0.5mv_i²

• Find the kinetic energy of the final velocity then subtract the kinetic energy of the initial velocity to get the change in kinetic energy.

If a question refers to where a force is applied on an object and/or the perpendicular component of force what type of problem is this?

Torque

If a question refers to the distance over which a force is applied and/or the parallel component of a force what type of problem is this?

Work and energy

Kinetic Energy = ?

½ mv²

• K = ½ mv²

What is the relation between net work and kinetic energy?

W_net = ∆K

• The net work of a system is equal to the change in kinetic energy.

What is the formula for ∆K?

∆K = ½ mv_f² - ½ mv_i²

• Just your run of the mill f-i but with kinetic energy!

Explain what the sign of work would be if the parallel force acts in the direction of motion. What about if it acts in the opposite direction of motion? What about if it acts perpendicular to the direction of motion?

• Same direction: Positive work, speeds up

• Opposite direction: Negative work, slows down

• Perpendicular: No work, 0.

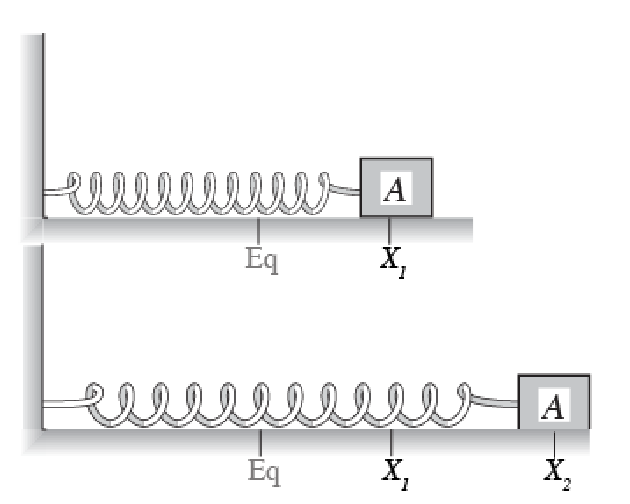
As the spring stretches to the right from x1 to x2, is the work done by the spring on the block positive, negative, or zero?

The spring force would be pointing to the left because it wants to return to original position…

• so spring force to the left, direction of motion right, work will be negative, the spring force is slowing down the motion.

What would be the expression for the work of a spring after it has traveled a distance x, with a spring constant k?

-½ kx²

• You have to know S = -k∆d, the change in distance is the x, so you’ll have S = -kx

• That is your force

What is the expression for the work done from x1 to x2?

W = -1/2 kx₂² + ½ kx₁²

• Basically just x2-x1 but the work done at x2 - the work done at x1.

What has a larger impact on kinetic energy velocity or mass?

K = ½ mv²

• Velocity has a larger impact on kinetic energy because it is squared.

Two hockey pucks are initially at rest on horizontal frictionless ice. Puck A has twice the mass of puck B, if they are pushed with the same constant force the same distance, how does the kinetic energy of puck A compare to puck B?

They are the same because W_net = ∆K

• The change in kinetic energy (both started at 0) is equal to the net work.

• You calculate the net work by multiplying the final force by the final distance and subtracting it from the initial force by the initial distance.

• Both pucks had the same force applied across the same distance thus had the same net work, so they would have the same kinetic energy at the end because they had the same change in kinetic energy from 0.

If the same force is applied to different massed pucks over the same time interval, which will move faster, the heavier or the lighter puck by the end?

F = ma

• The lighter puck will move faster by the end because the acceleration will equal the force divided by a lighter mass.

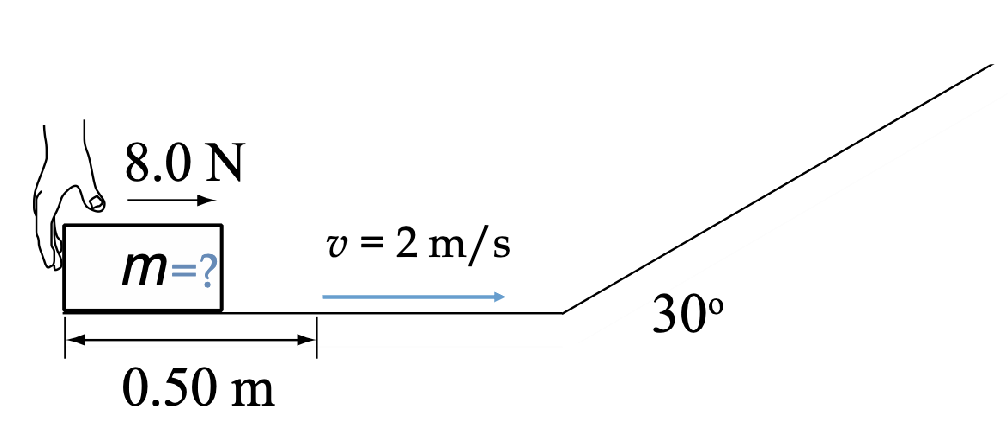
If the initial velocity of this block is 2m/s when it hits the incline, how would you find how high (y) the block gets?

W_net = -mgy

• Remember because the only work being done on the block is gravity because no friction and no other force it was let go.

W_net = -mgy = ∆K

• ∆K = ½ mv_f² - ½ mv_i²

• We know the final velocity will be 0 when it slows to a stop up the incline so…

-mgy = -½ mv_i²

• Isolate for y and you should get 0.204 m!

(no friction) What is the net work when you let the box go and it goes up the ramp?

Net Work = -mgy

• The only force acting on the box is gravity and it is pulling against the direction +Y, hence negative work.

(no friction) What would be the net work if the box were going DOWN an incline?

Net Work = mgy

• The force of gravity would contribute positive work to the box moving down, and the only force acting on it would be gravity.

(no friction) What would be the net work if the box were just pushed and let go in the horizontal direction? You aren’t pushing it anymore you let go…

Wnet = 0

• Gravity is the only force acting on the box and it is perpendicular to the motion, thus the work is 0.

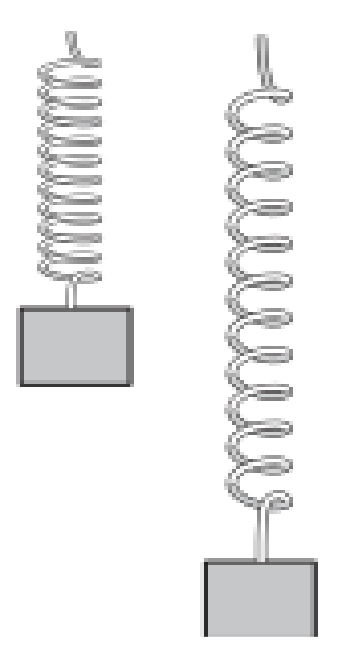
A spring with a mass attached to it is held up then let go. What is the change in kinetic energy from the top to the bottom (where it is stretched its furthest)?

What is the net work done on the block from t=0 to the time that it reaches its full stretch?

How many forces act on the block?

• The change in kinetic energy is 0 because it starts at 0, gets to a peak kinetic energy, then begins increasing potential energy until kinetic energy is 0 again at the bottom.

• The net work is thus also 0 because it does an equal amount of work in the direction then away from the direction to get the block to that full stretched position.

• Two forces act on the block, gravity and the spring force.

If mass is 0.5 kg, the spring constant k is 32, how far (y) does the block travel from rest to its fully stretched form?

Remember, the ∆K from t=0 to the time it is fully stretched is 0 because the initial velocity is 0 and the final velocity is 0.

• W_net = ∆K = 0

The W_net is done by two forces, the force of gravity and the spring force. The force of gravity acts in the same direction as the motion, down.

• So W_gravity = mgy

The spring force acts in the opposite direction of the motion, up.

• So W_spring = -½ky² (we know y is the distance traveled)

Combine the two and get…

• mgy -1/2ky² = 0

Isolate for y and you should get 0.306, so 30.6 cm.

• Additionally: The initial velocity and final velocities are both 0 which means that the ∆K is 0. There are two forces acting on the box in both stages, a spring force and the weight of gravity. to calculate the work we say the force multiplied by the distance it has been applied, so for gravity you say mg*y and that is working in the direction of the distance so it is positive. The spring force is -1/2ky² (where y is the distance) and it is negative because the spring force opposes the direction of the motion.

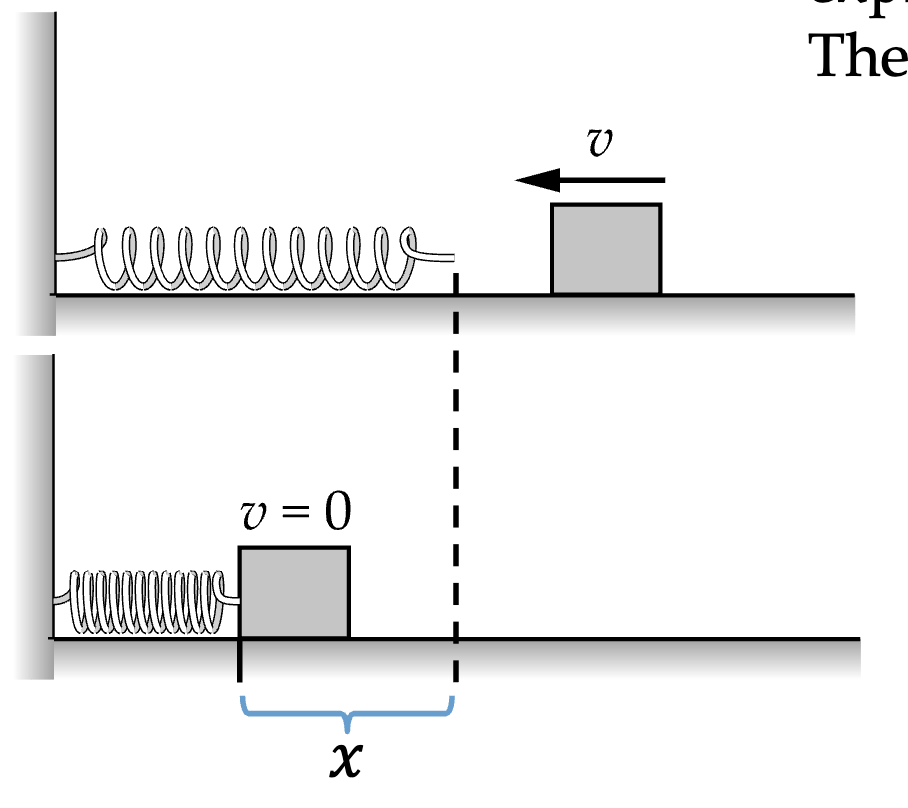
What is the proper expression for relating the work kinetic energy theorem for the block: W_net = ∆K

W_net

• The only force acting on the block is the spring force for that distance x, in the opposite direction of the distance, so -1/2kx²

∆K

• Kinetic energy is equal to 1/2mv², so ∆K is equal to 1/2mvf² - 1/2mvi²

• final velocity is 0

• -1/2mvi²

W_net = ∆K

-1/2kx² = -1/2mv²

internal vs external forces? When can we only define potential energy?

Internal forces are within the system. External forces are outside of the system and alter the amount of energy in the system.

• Potential energy can only be defined when there is a force that is internal to the system and conservative.

• This means that the force is within the system and is path independent meaning only the initial and final positions matter.

For a conservative internal force, every bit of energy lost from kinetic energy becomes stored as potential energy, and vice versa.

The formula for kinetic energy is always the same, and potential energy + work are "opposites" for conservative forces.

What is the formula for potential energy of a spring? What is the formula for potential energy of gravity?

U_s = 1/2kx²

U_g= mgy

• Kinetic energy is always 1/2mv²

• W_net for the spring and gravity is just the opposite of the potential energy formula.

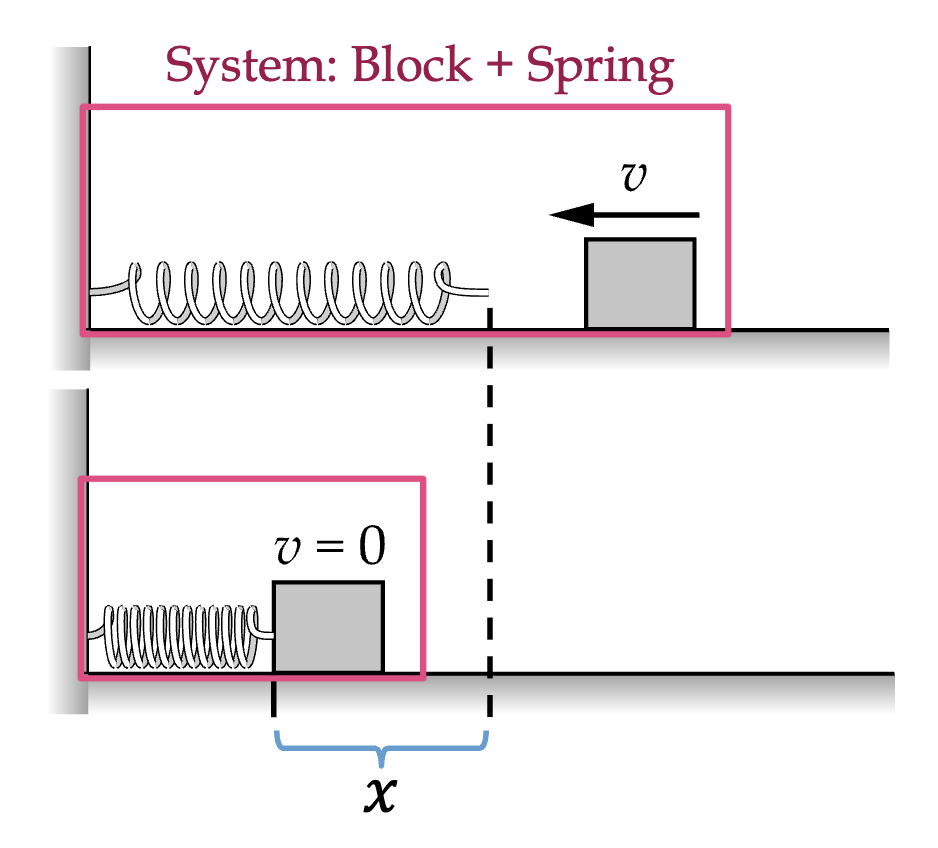
What is the ∆U (change in potential energy of the block)

∆U (spring) = 1/2kx²

W_net (spring) = -1/2kx²

Remember, they are opposites…

• ∆U = Uf - Ui

• 1/2kx² - 1/2k(0)²

  • Initially the spring has been compressed 0, so Ui is equal to 0. The potential energy rises the more that the spring is compressed because the spring force points in the direction of that potential energy!

∆U = 1/2kx²

What is the formula for the net external work in terms of kinetic and potential energy?

W_net,external = ∆K + ∆U

• The net external work is equal to the change in kinetic energy plus the change in potential energy. Whatever external work you add to the system will cause a change in kinetic or potential energy, and if you add those changes up you’ll see how much work was done on the system.

if an object is moving at a constant speed what is the net work being done on that object?

0!

What is the work done by gravity if our block is falling down and our system is just the block? How would this be different if our system was the block and earth?

• The block falling is gravity doing positive work when the system is just the block.

• The block falling when the system is the earth and the block has no work by gravity on it, rather, the gravity is converting gravitational potential energy into kinetic energy.

• No work is going into or out of a system.