Intensity Transformations and Histogram Processing

principal objective of image enhancement

process an image so that the result is more suitable than the original image for a specific application

image enhancement approaches

spartial domain methods

frequency domain methods

Spatial domain

refers to the image plane itself, based on direct manipulation of pixels in an image

spatial domain equation

g(x, y) = T[f(x, y)]

f(x, y) is the intensity of input image at pixel (x,y),
g(x, y) is the intensity of processed image at pixel (x,y)

frequency domain

based on modifying the Fourier transform of an image

Point Operations in Spatial Domain + formula

simplest image enhancement technique, work through pixel-by-pixel basis

Each output pixel’s value depends only on the corresponding input pixel value

s=T(r)

• r: Input pixel intensity.

• s: Output pixel intensity.

• T: Transformation function

types of point operations

image negatives

log transformations

power-law(gamma)

piecewise linear- contrast stretch/gray level slicing

image negative formula + explanation

s = L-1-r

• used for enhancing bright detail embedded in dark regions, esp when dark areas dominant in size

log transformations formula + explanation

s = c log (1 + r)

• enhances low intensity values

• maps a narrow range of low gray-level values in the input image into a
  wider range of output levels

Power-Law Transformations formula + explanation

s=c⋅rγ

• adjust intensity

• gamma < 1 brightens, > 1 darkens

Piecewise-Linear Transformations definition and types

multiple linear segments to adjust intensity

require user input to define the breakpoints and slopes

types:

• contrast stretching

• gray level slicing

• bit plane slicing

contrast stretching

• Expands the dynamic range of an image

• Useful for low-contrast images caused by poor illumination or sensor issues

• locations of points (r₁,s₁) and (r₂,s₂) control the shape of the transformation function

• r₁<=r₂ and s₁<=s₂ is assumed so that the function is single valued and monotonically increasing

gray level slicing

• Highlights specific ranges of gray levels while suppressing others

• Applications: Medical imaging, satellite imagery

bit plane slicing

• Separates the image into its bit-planes to emphasize individual bits. / determine the adequacy of the number of bits used to quantize each pixel

• Applications: Image compression, noise analysis.

Histogram Processing def + formulas

• histogram represents the frequency of each intensity value in an image

• involves analyzing and modifying this distribution to enhance image quality

• formulas

  • unnormalized hist in [0, L-1] → h(r_k)= n_k

  • normalized hist → p(r_k) = n_k/MN

  • r_k = k^th gray value

  • n_k = number of pixels having gray level r_k

histogram processing techniques

• histogram equilization

• histogram matching

histogram equilization

• Enhances the contrast of an image by redistributing intensity values to occupy the entire dynamic range more evenly

• Uses the cumulative distribution function (CDF) to map original pixel values

• discrete formulas work with probablities and summations vs. cont. integrals

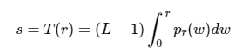
Histogram Matching (Specification)

• Adjusts the image histogram to match a specified target histogram

• Useful when uniform redistribution isn’t ideal

If you wanted to improve the contrast in an image with a very narrow range of intensity values, which technique would you use: histogram equalization or histogram matching?

Histogram equalization would be the right choice because it redistributes the intensity values more evenly across the full range, enhancing the contrast. This is particularly effective when the image has a narrow range of intensity values, as it spreads out the pixel distribution

Histogram Equalization Example:

Given an 8-pixel image with gray levels in the range [0, 7]: [0,0,1,1,2,3,5,7], Find the histogram-equalized image

1. Compute the Histogram: Count the frequency of each gray level:

   • [gray level (r_k​), freq (n_k)]

     [0, 2]

     [1, 2]

     [2, 1]

     [3, 1]

     [4, 0]

     [5, 1]

     [6, 0]

     [7, 1]

2. Calculate the Probability (p(r_k)): Normalize the histogram by dividing by the total number of pixels (N=8) → p(r_k) = n_k/8:

   • [gray level (r_k​), freq (n_k), p(r_k)]

     [0, 2, 0.25]

     [1, 2, 0.25]

     [2, 1, 0.125]

     [3, 1, 0.125]

     [4, 0, 0]

     [5, 1, 0.125]

     [6, 0, 0]

     [7, 1, 0.125]

3. Compute the Cumulative Distribution Function (CDF): CDF(r_k​) = ∑ (j=0 → k) p(r_j)

   • [r_k, CDF(r_k)]

     [0, 0.25]

     [1, 0.5]

     [2, 0.625]

     [3, 0.75]

     [4, 0.75]

     [5, 0.875]

     [6, 0.875]

     [7, 1.0]

4. Map to New Gray Levels: The new gray level is computed as: s_k​ = round((L−1)⋅CDF(r_k​)), where L = 8

   • [r_k, CDF(r_k​), s_k​]

     [0, 0.25, 1]

     [1, 0.5, 3]

     [2, 0.625, 4]

     [3, 0.75, 5]

     [4, 0.75, 5]

     [5, 0.875, 6]

     [6, 0.875, 6]

     [7, 1.0, 7]

5. Resulting Image: Replace each r_k in the original image with s_k​:

   • [0,0,1,1,2,3,5,7]→[1,1,3,3,4,5,6,7]

Histogram Matching Example

Match the histogram of the image from above to a target histogram with the following probabilities:

• [Gray Level (z_q), p_z(z_q)]

  [0, 0.125]

  [1, 0.125]

  [2, 0.25]

  [3, 0.25]

  [4, 0.125]

  [5, 0.125]

1. Compute the Target CDF: G(z_q) = ∑ (j=0 → q) p_z(z_j)

   • [Gray Level (z_q), G(z_q)]

     [0, 0.125]

     [1, 0.25]

     [2, 0.5]

     [3, 0.75]

     [4, 0.875]

     [5, 1.0]

2. Map r_k​ to s_k​ (Equalization Step): Use the equalized mapping from equalization

3. Match s_k to z_q: Find the closest value of G(z_q) for each s_k:

   • [s_k, G(z_q), z_q​]

     [1, 0.25, 1]

     [2, 0.5, 2]

     [3, 0.75, 3]

     [4, 0.875, 4]

     [5, 1.0, 5]

4. Resulting Image: Replace each s_k in the original image with z_q​:

   • [1,1,3,3,4,5,6,7]→[1,1,2,2,2,3,4,5]