Oscillations

Simple harmonic motion (SHM) is a mechanical process that is characterised by the following conditions:

‣ The object oscillates either side of an equilibrium position

‣ A restoring force always acts towards this equilibrium position

‣ The force is proportional to the object's displacement

‣ Consequently the object has an acceleration proportional to its displacement and in the opposite direction

The defining equation for SHM is:

F = -K x

where 'x' is displacement and 'k' is a constant.

Understand the following terms in context of SHMωL

‣ The frequency is the number of full cycles that occur each second.

‣ A full cycle is the motion from maximum positive displacement, to maximum negative displacement and then back to the maximum positive displacement again.

‣ The time period is the length of time it takes to complete a cycle

Like in circular motion, SHM makes use of ω, the angular frequency.

Be able to apply the following equations when analysing SHM scenarios:

ω = 2πf

T = 1/f = 2π/ω

a = -ω²x

x = Acosωt

v = -Aωsinωt

a = -Aω²costωt

Make sure you are careful to substitute 'a' with acceleration and 'A' with maximum displacement.

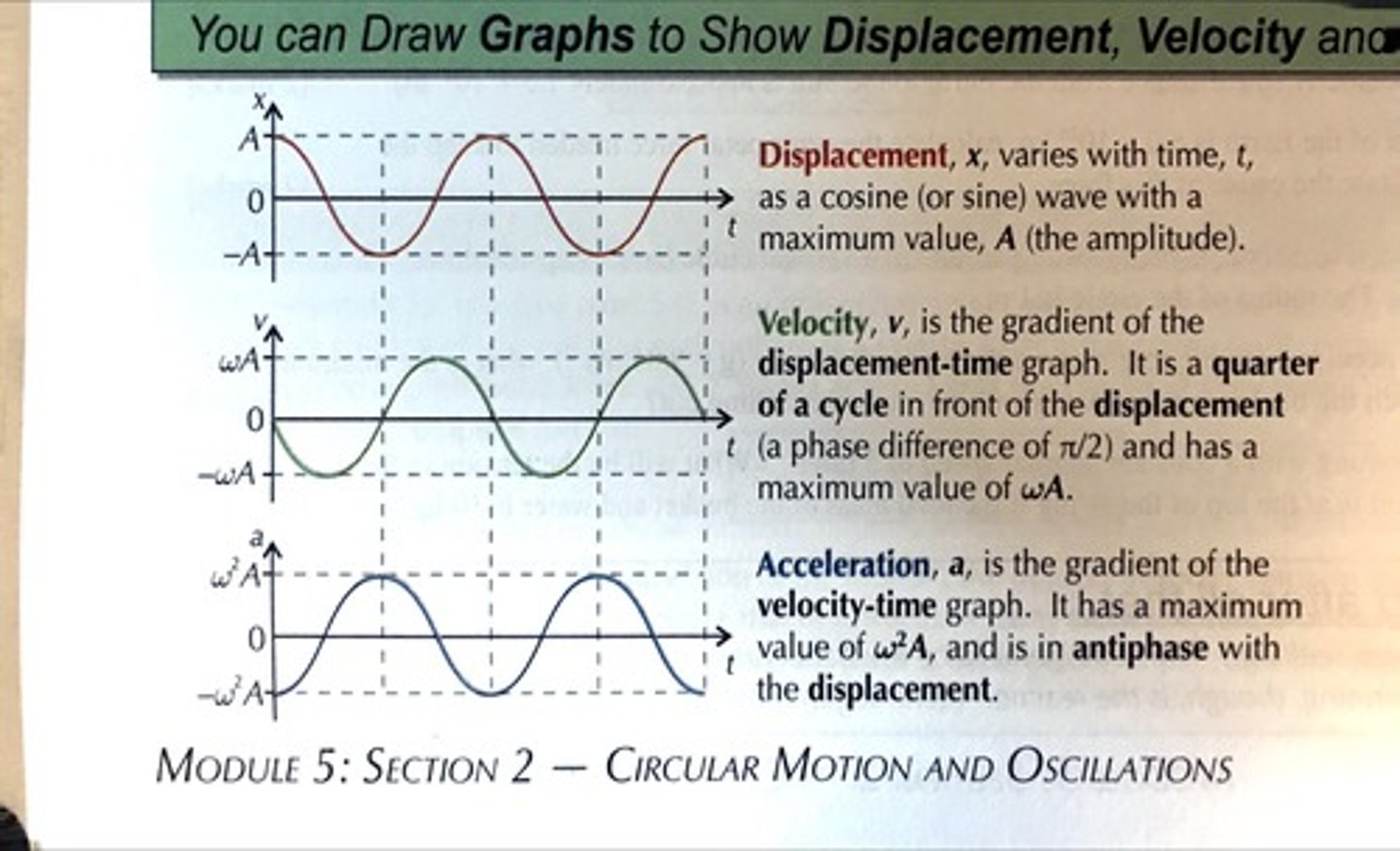
SHM graphs:

Displacement-time graphs = The gradient at a given point on this graph gives the velocity that the object is moving at

Velocity-time graphs = The gradient at a given point on this graph hives the acceleration that the object is moving at.

Displacement and velocity -time graphs for objects oscillating with SHM.

A spring oscillator consists of a mass on a spring which oscillates with simple harmonic motion.

The time period of oscillation for a spring oscillator is given by:

T = 2π√m/k

The period of oscillation for a spring oscillator isn't affected by the gravitational field strength. This means that the period will be the same for all initial displacements.

A pendulum oscillator consists of a mass on a string which oscillates with simple harmonic motion.

The time period of oscillation for a pendulum oscillator is given by:

T = 2π√l/g

The period isn't affected by the object's mass. This means that the period will be the same regardless of how heavy the mass is.

It is also unaffected by the magnitude of displacement, meaning the period will be the same for all initial displacements

When an object oscillates with SHM, energy is transferred between kinetic and potential energies.

These transfers are as follows:

‣ At maximum positive displacement, the potential energy is at a maximum.

‣ As the object travels towards the equilibrium position, potential energy is transferred to kinetic energy as the object accelerates.

‣ At the equilibrium position, the kinetic energy is at a maximum and the potential energy is at a minimum

‣ At maximum negative displacement, the potential energy is again at a maximum, while kinetic energy is at a minimum

The energy transfers that occur in SHM can be graphed:

Assuming no damping occurs:

Eₖ+Eₚ = total energy and it is constant unless damping occurs.

There are two maximum point of Eₖ and Eₚ per cycle.

Damping of a SHM system occurs when energy is transferred out of the system. This results in the total energy no longer being constant.

In reality all system will experience some form of damping force, such as:

- Friction between components

- Air resistance

Systems are often also deliberately damped. Examples of this are:

- Car suspension systems

- Springed doors to prevent slamming

- Swings

- Speedometer dials

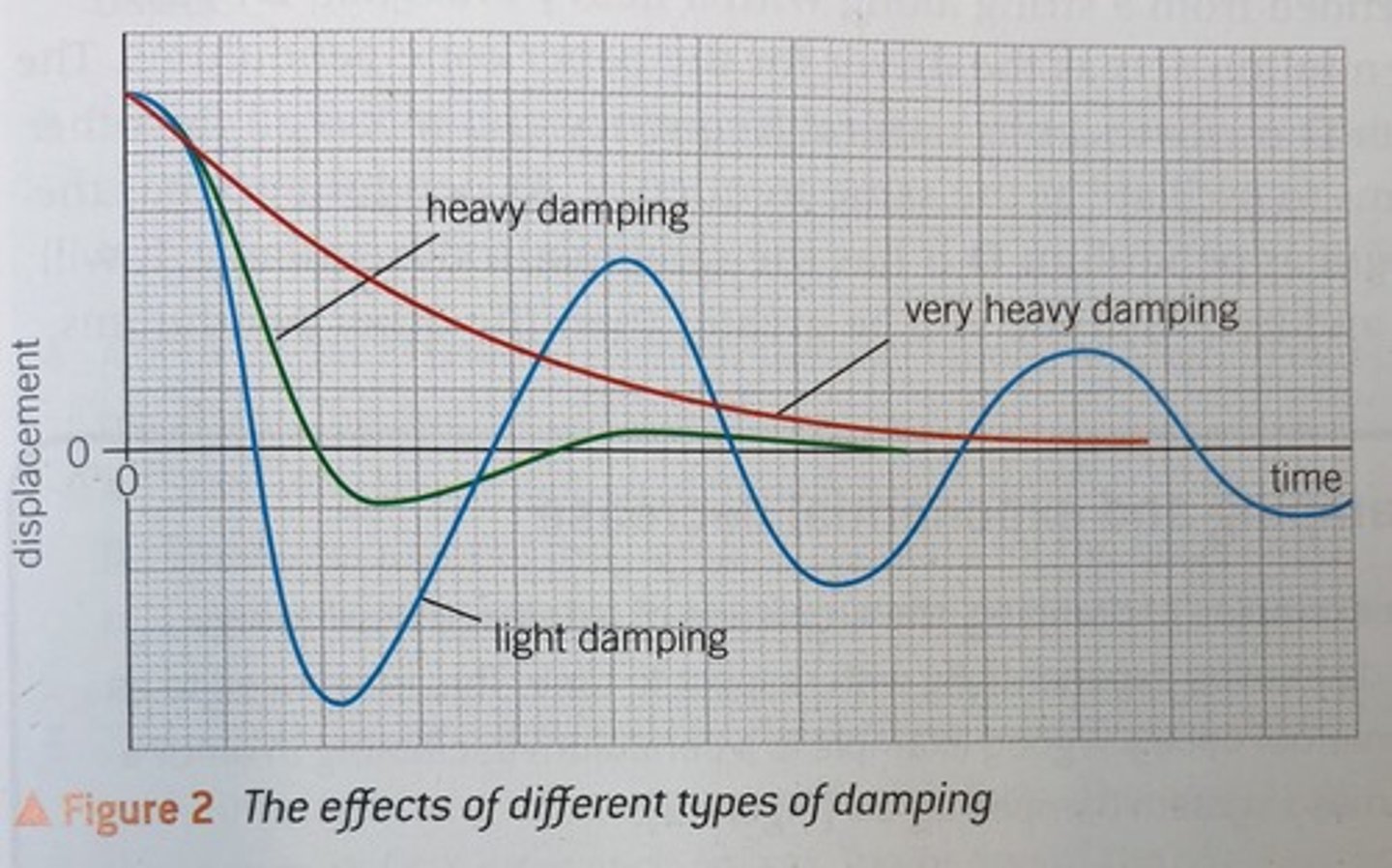
Types of Damping:

There are three main types of damping that you need to be aware of:

1. Light Damping

2. Critical Damping

3. Overdamping

1. Light damping is where the oscillations are reduced slowly, and is normally the type of damping caused by resistive forces such as air resistance and friction.

2. Critical damping involves stopping the oscillations and returning to the equilibrium in the quickest time possible.

3. Overdamping is caused when the damping force is greater than that for critical damping, and stops the oscillations, but takes longer to return to the equilibrium position.

Vibrations:

The vibrations that occur in SHM can be one of two types:

1. Free vibrations

2. Forced vibrations

1. Free vibrations: The frequency a system tends to vibrate at in a free vibration is called the natural frequency.

2. Forced vibrations: A driving force causes the system to vibrate at a different frequency. For higher driving frequencies, the phase difference between the driver and the oscillations rises to π radians. For lower frequencies, the oscillations are in phase with the driving force. When resonance occurs, which is where energy is most efficiently transferred to the system, the phase difference will be π/2 radians.

Resonance takes place when the driving frequency is equal to the natural frequency of the system. You should know that at resonance:

- The rate of energy transfer is at a maximum

- The driving force is π/2 out of phase and ahead of the oscillations

- The amplitude of oscillation is at a maximum

In some situations resonance is desirable such as for musical instruments, however in other situations resonance is undesirable. Bridges and towers often have to be damped so that footfall or earthquakes don't produce oscillations at the structure's natural frequency. This is because the large amplitude oscillations caused by resonance could damage the structure.

What are the two conditions required for an object to oscillate with SHM?

1. The restoring force is directly proportional to the displacement.

2. The restoring force always acts towards the equilibrium position.

What is angular frequency?

Angular frequency is a measure of the rate of rotation of an object.

Give two equations for angular frequency.

ω = 2π/2

ω = 2πf

What are two types of oscillations that an object can experience?

1. Free oscillations

2. Forced oscillations

What is the frequency of a freely oscillating object equal to?

Freely oscillating objects will vibrate at their natural frequency.

What is resonance?

Resonance is where the amplitude of oscillations of an object drastically increase due to gaining an increased amount of energy from the driving force.

This occurs when the driving frequency equals the natural frequency of the object.

What can be said about an object undergoing resonance?

The object will be oscillating at its maximum amplitude and the rate of energy transfer is at a maximum

What is damping?

Damping occurs when energy energy is lost from and oscillating system due to an external force acting on it.

What are the three types of damping?

1. Light Damping

2. Critical Damping

3. Heavy Damping

What is critical damping?

Critical damping is when the damping causes the object to return to the equilibrium position in the quickest time possible without oscillating.

State the equation for the total energy stored in a simple harmonic oscillator.

Energy stored = ½ kA²

where k is the spring constant, and A is the amplitude.

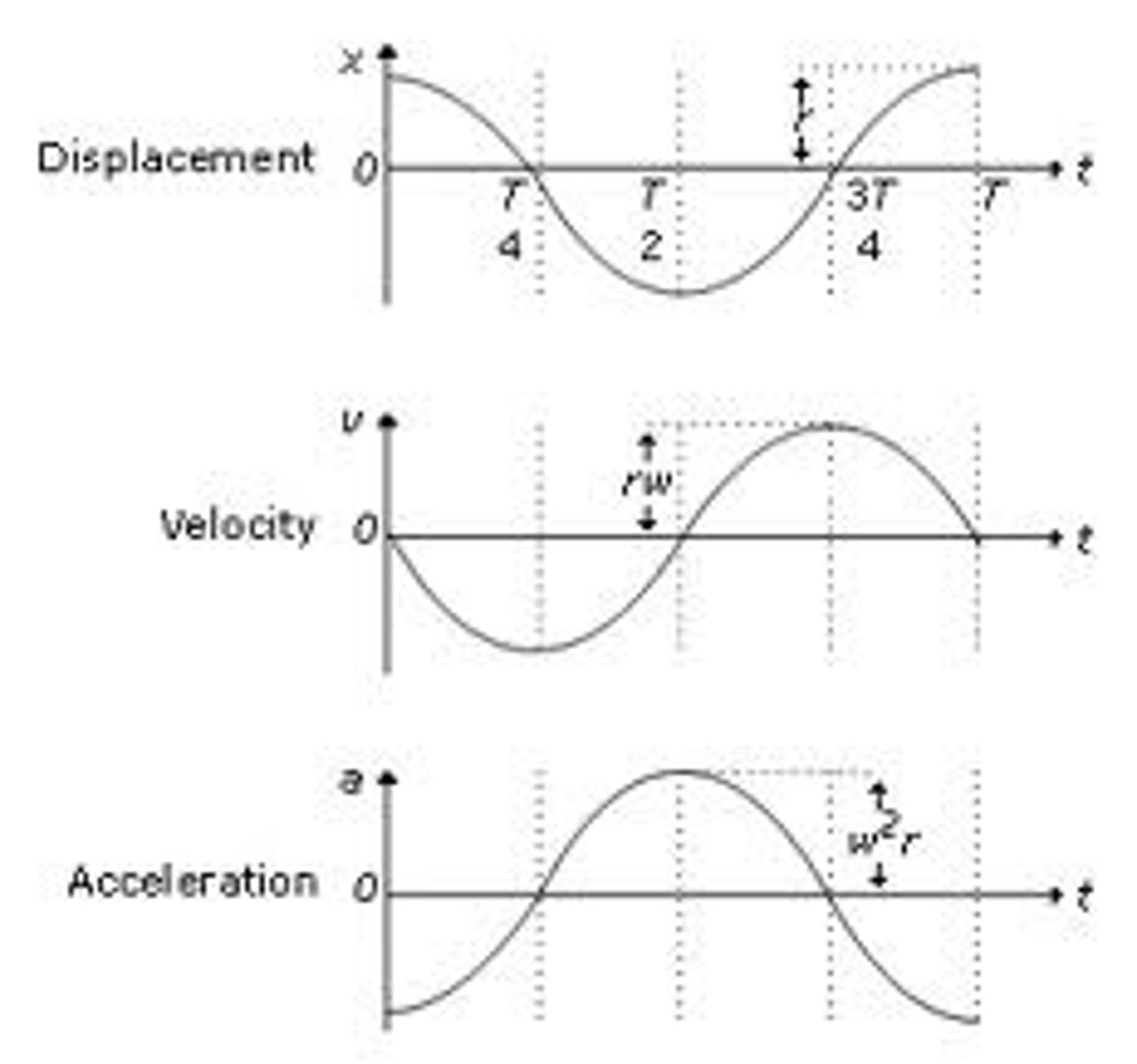
If the following graph shows displacement against time, what would the velocity-time graph and acceleration-time graphs look like?

What is the difference between free and forced oscillations?

When an object oscillates without any external forces being applied, it oscillates at its natural frequency. This is known as free oscillation. Forced oscillation occurs when a periodic driving force is applied to an object, which causes it to oscillate at a particular frequency.

How can time period be calculated for a mass-spring system and a pendulum respectively?

T = 2π√m/k

For a mass-spring system where m is mass/kg and k is the spring constant/Nm⁻¹

T = 2π√l/g

For a pendulum where l is the string length/m and g is the gravitational field strength /ms⁻²