Differential Equations Formulas to Know

Linear first order

General form for linear ODEs

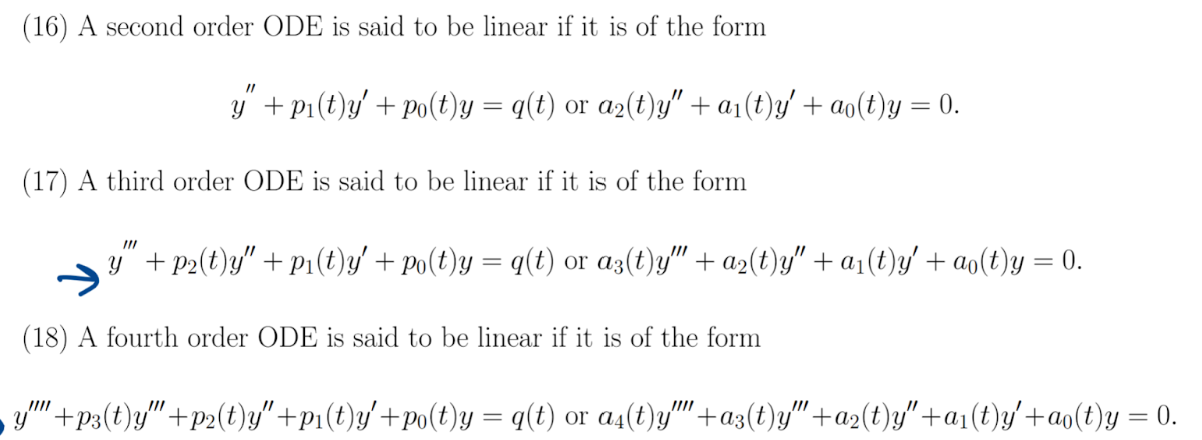
First order autonomous ODE

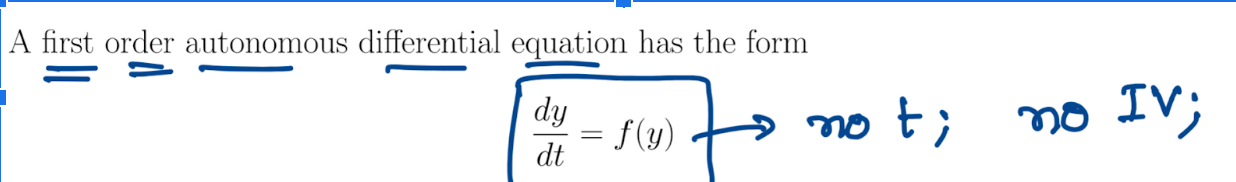
Separable form

Soln to homogenous first order linear

Homogenous ODE solving

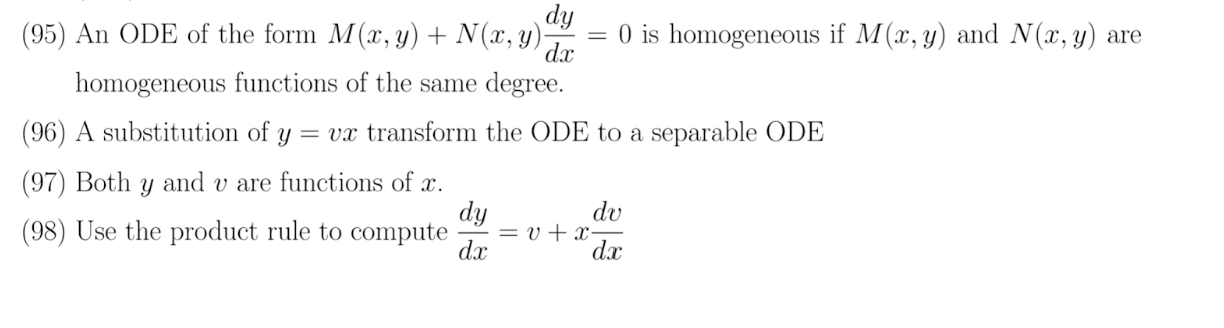
Bernoulli Equations

Solving Bernoulli Equations

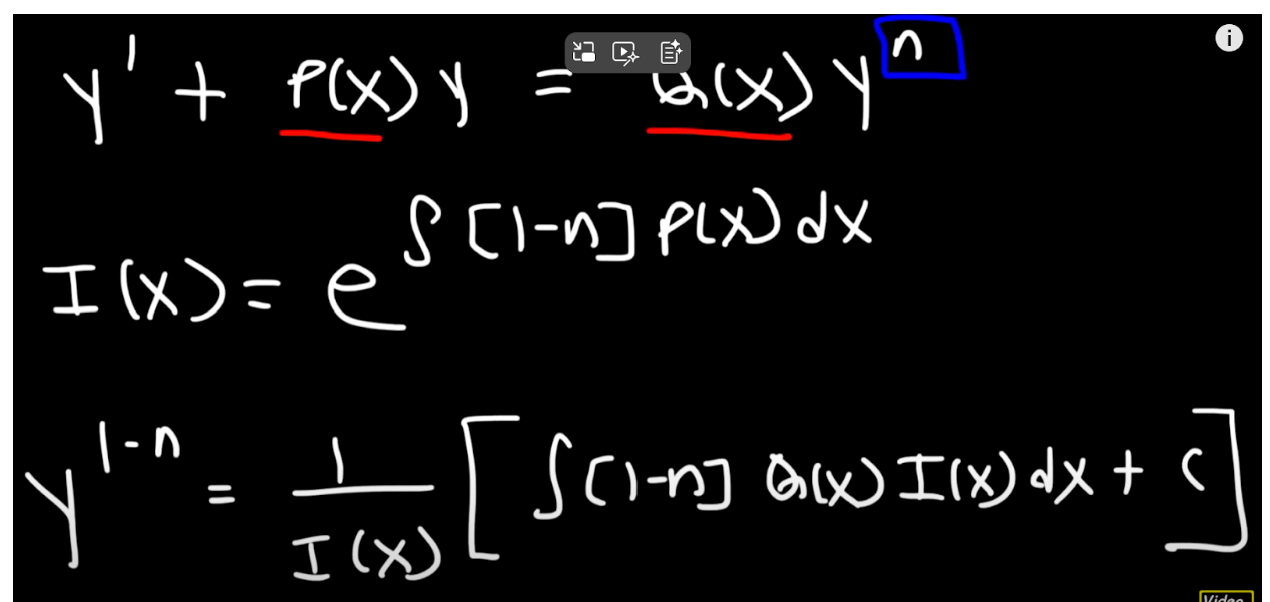
Population growth equation

What is the Wronskian?

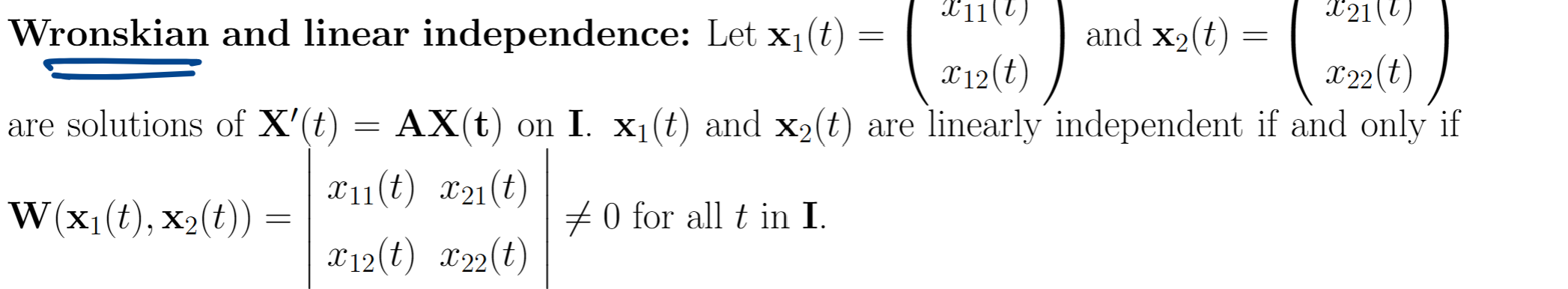
Fundamental solution set

If two vectors have a Wronskian that is not zero, they are linearly independent. Therefore, they form a basis for all solutions in the space.

Why is having a fundamental solution set for a differential equation space important?

• The general solution built from a fundamental set of solutions is like the "master formula" that covers all possible behaviors of the system.

• Once you have it, you can plug in constants c1,c2,…c_1, c_2, ​,c2​,… determined by initial conditions

• That’s what lets you go from the abstract math solution to the specific trajectory of the system in the real world.

If you don’t have a fundamental set, you’re missing part of the solution space, and there will be some initial conditions you simply can’t represent.

Process for solving x’ = Ax (for 2×2 matrices)

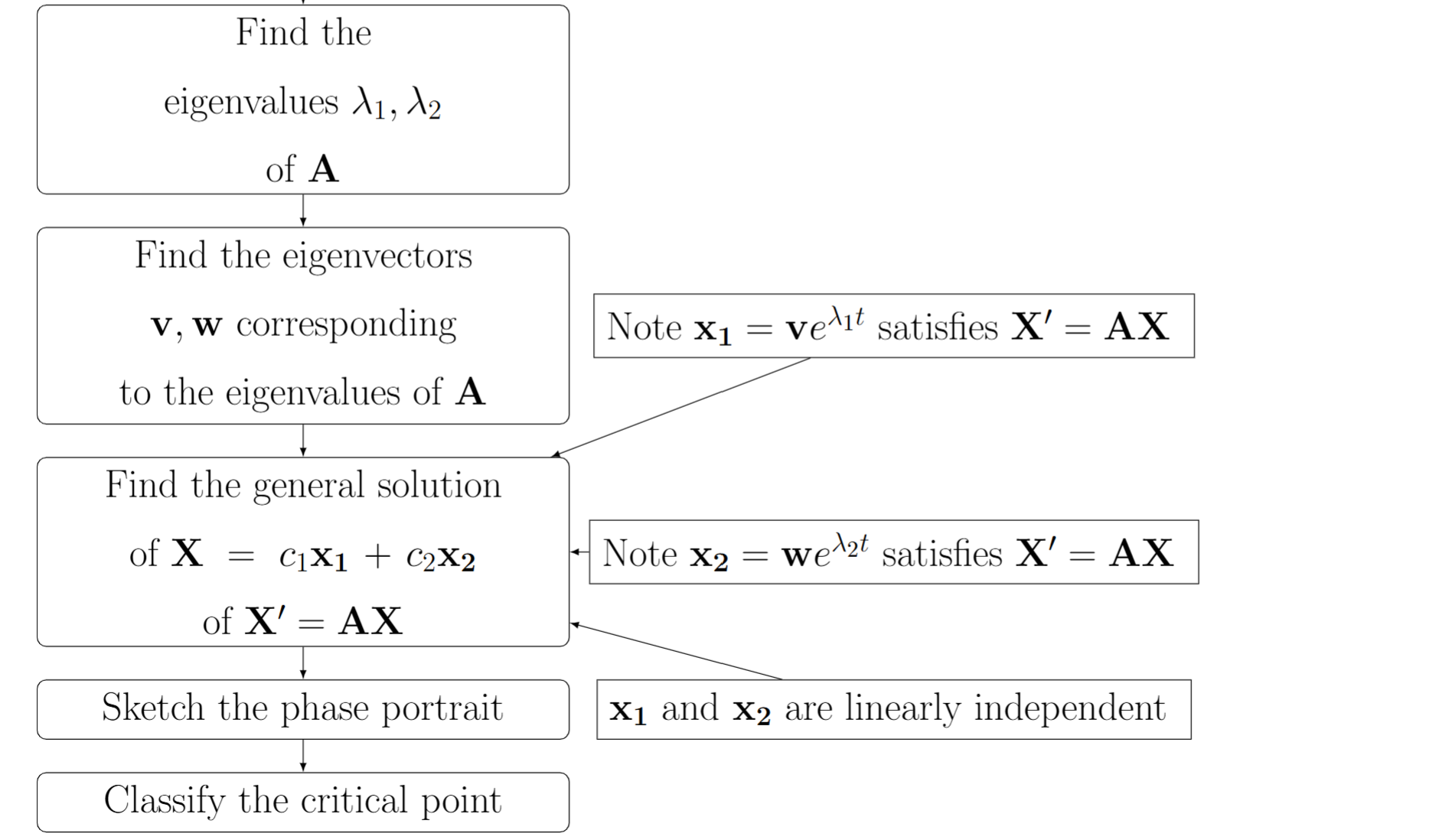
General solution to x’ = Ax

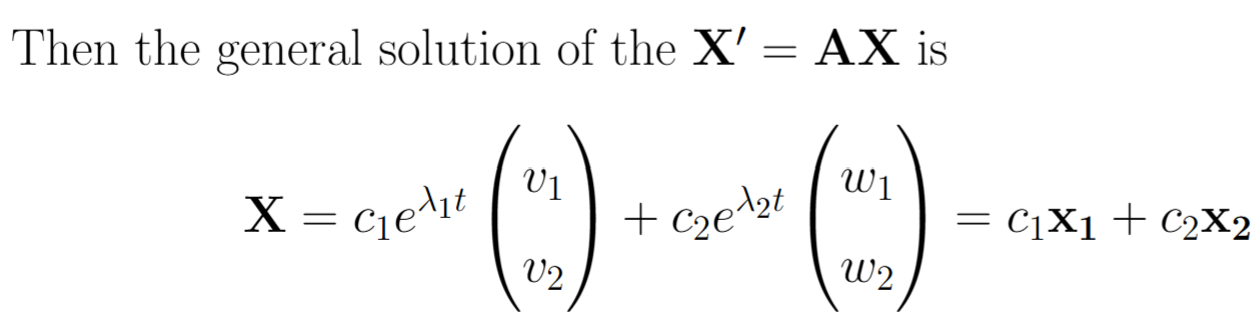
Phase portrait for two positive, distinct eigenvalues

Phase portrait for two negative, distinct eigenvalues

Phase portrait for two dif sign eigenvalues

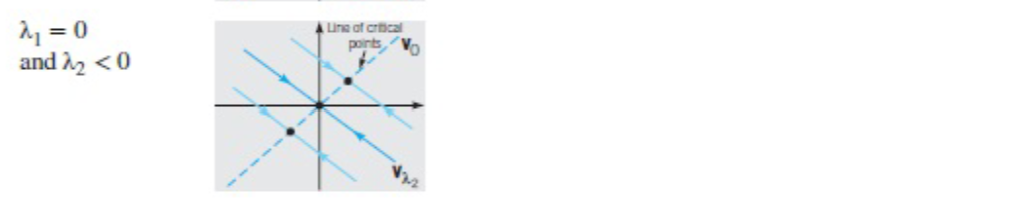
Phase potrait for lamda = 0 and positive lamda

Phase potrait for lamda = 0 and negative lamda

If an equilibrium is stable in a phase portrait…

All solns will “crash in“ on that point

In equilibrium is unstable in a phase portrait…

All solns will “run away“ from that pt

Why do phase portraits exhibit an exponential behavior?

Why does negative eigenvalues create a stable node for soln?

Saddle point, why?

Along negative eigenvalue, solution is pointing toward fixed point and along another solution is pointing away from fixed point

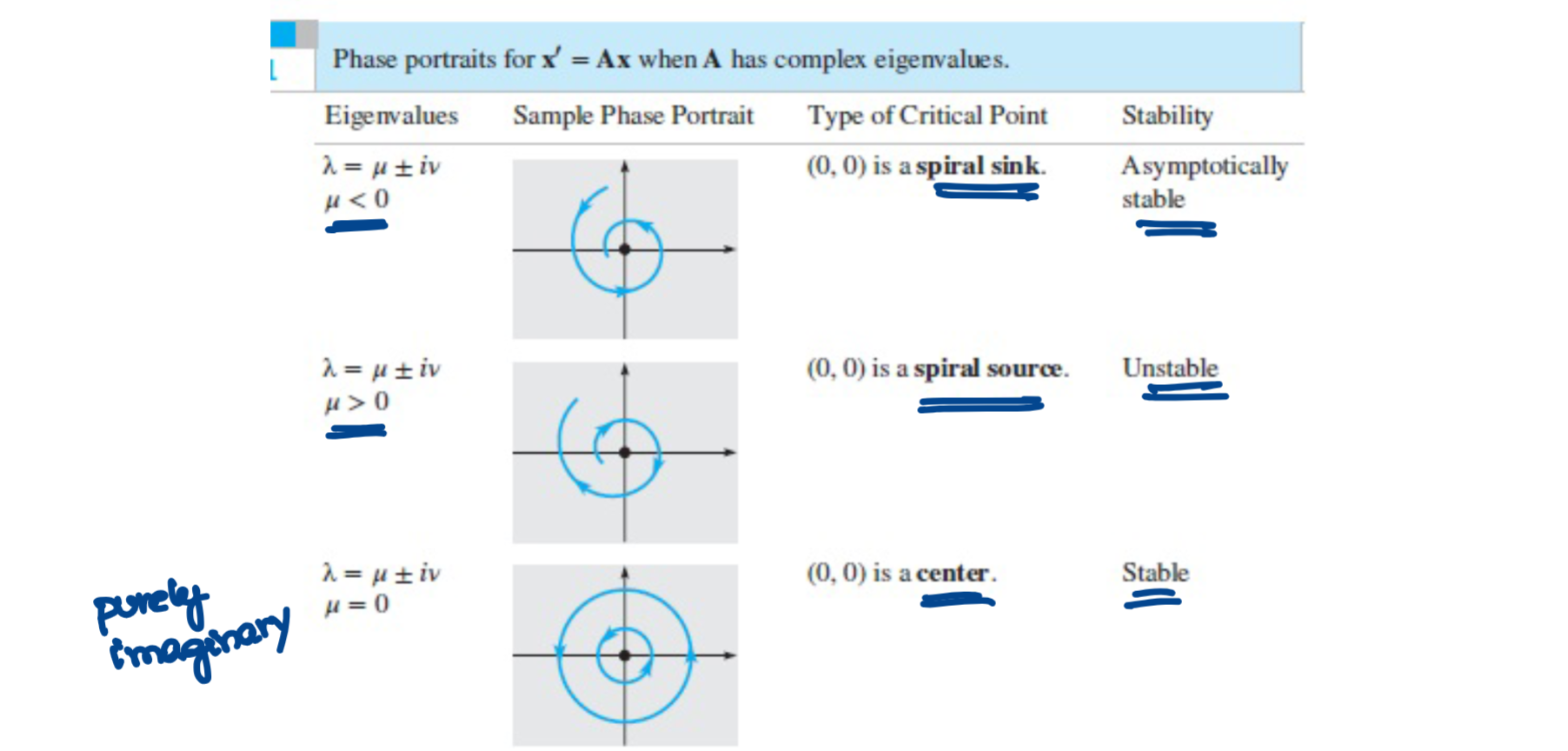
Complex eigenvalue, positive real component

Unstable spiral (away from origin)

Complex eigenvalue, negative real component

Stable spiral (toward origin)

General solution for complex eigenvalues

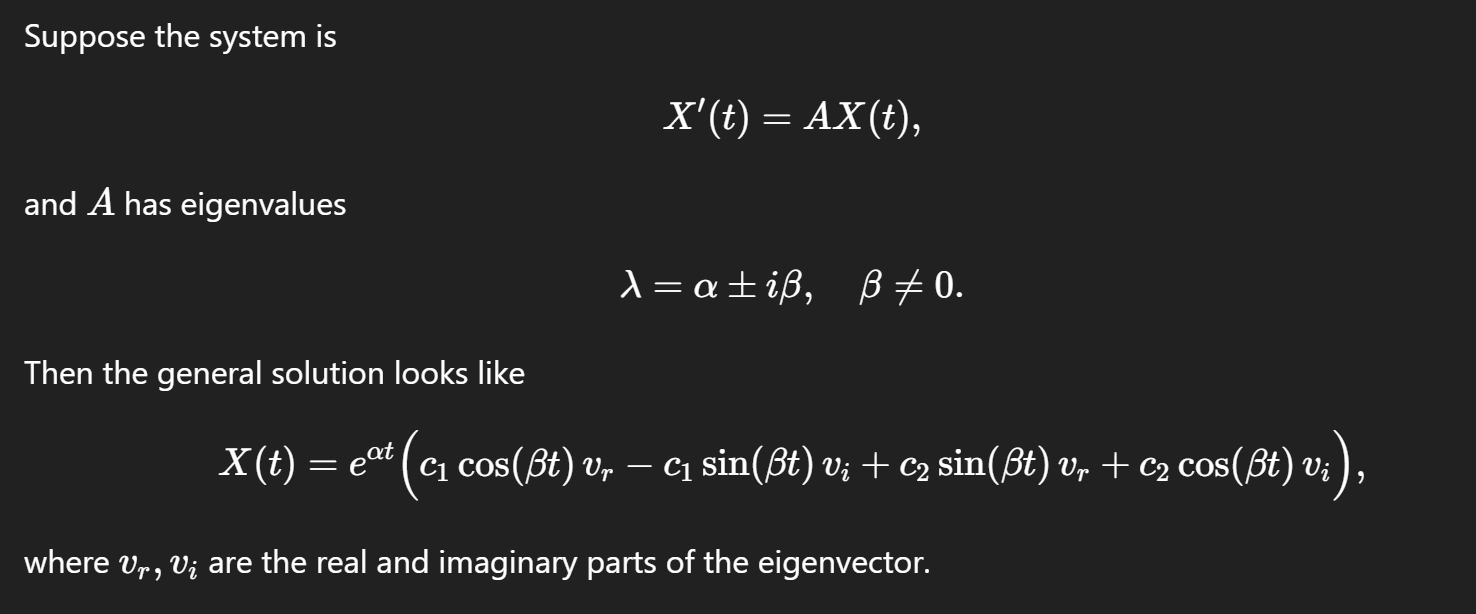
Why sin and cos with complex eigenvalues

For a 2×2 matrix, if the determinant is not 0, where is the critical point?

Just the origin. No other point where the derivative can equal zero

Why eigenvalues after finding critical point?

So you can see the behavior of this equilibrium point

Phase portrait of lineardly depedent vectors

Collapsed onto a lower dimension (like a line) because does not have a fundamental set for the full ___ dimmensions

why are there multiple lines running around in phase portraits

Initial value not yet specified: “"general solution”

Eigenspace of eigenvector in phase portrait

Just the line of the eigenvector associated with the eigenvalue

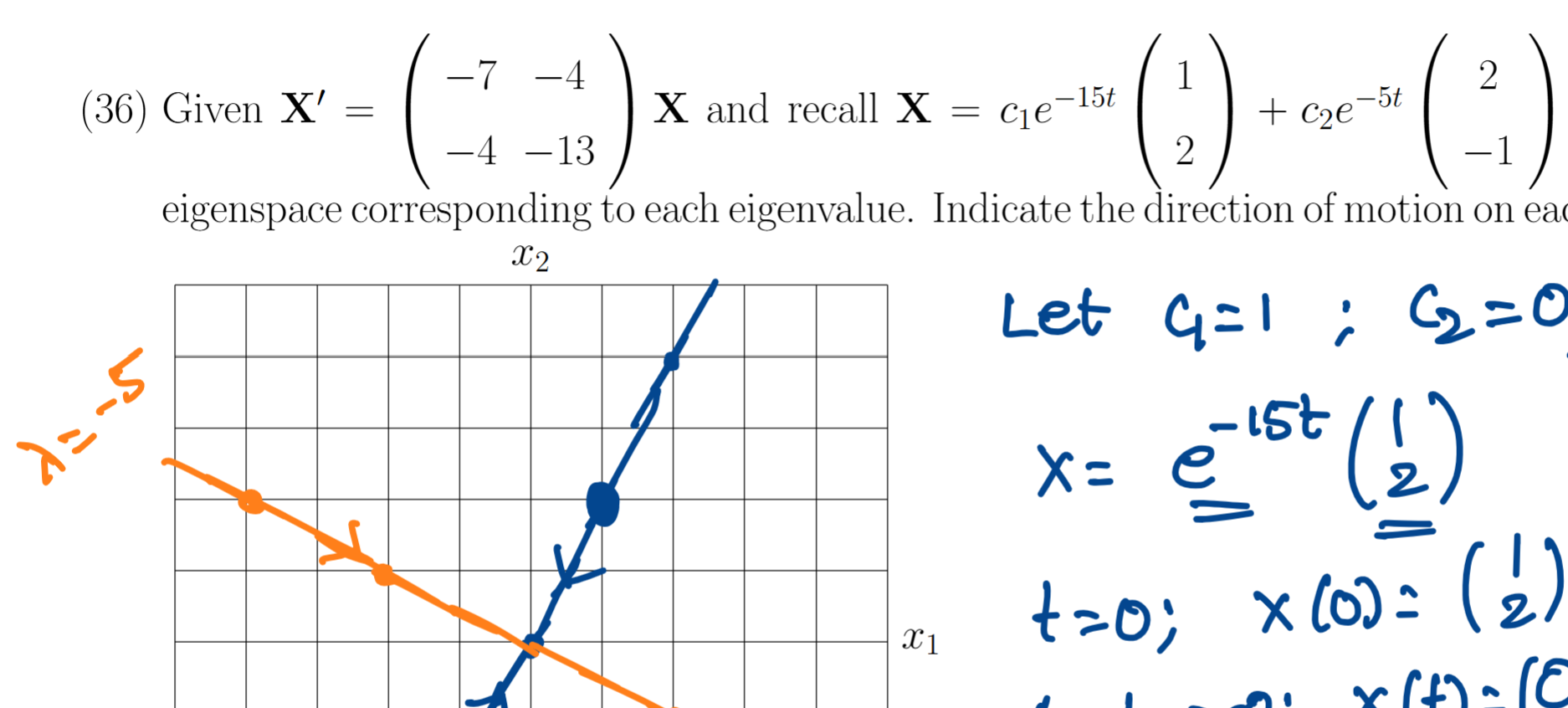
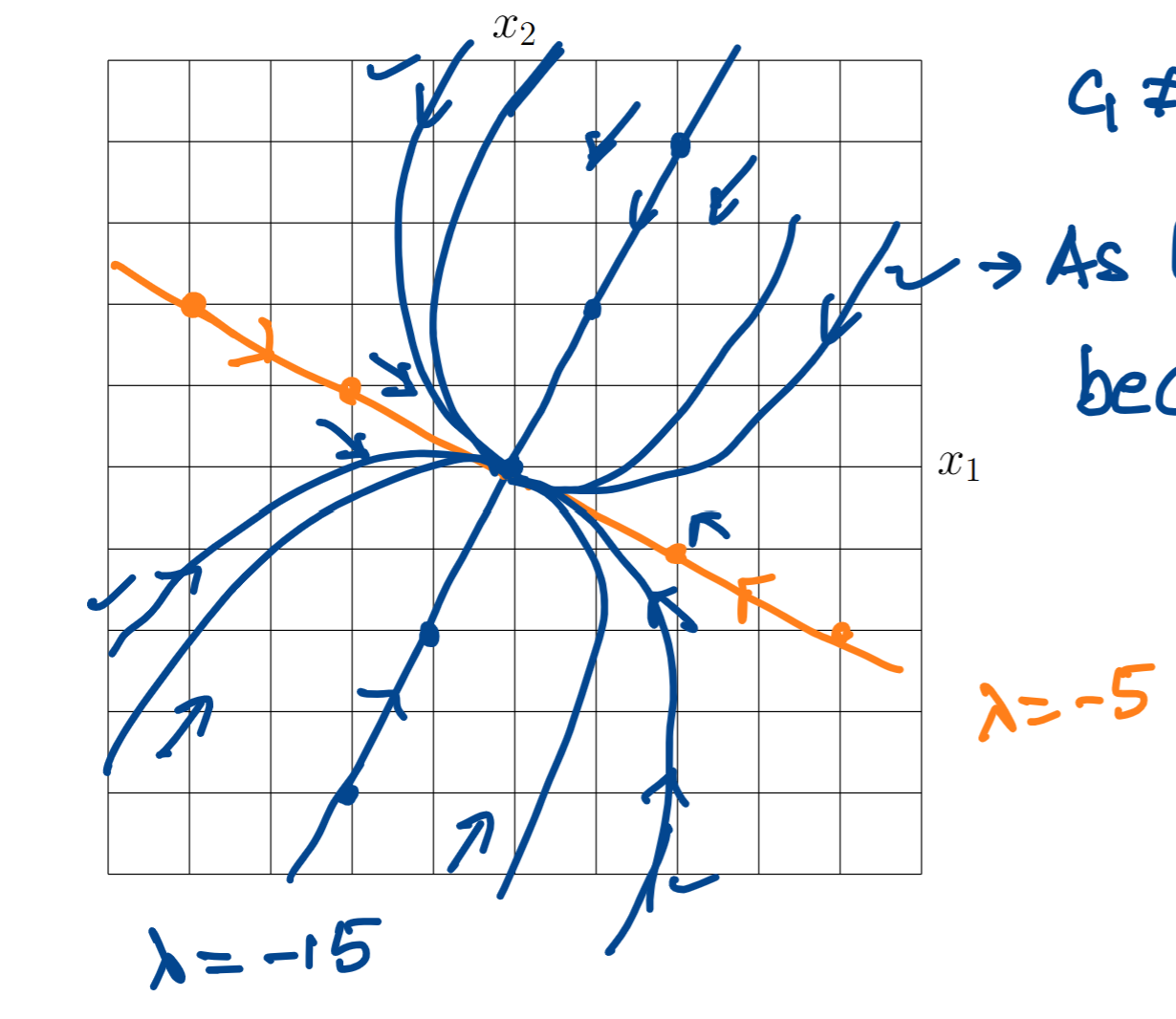
Why the bowl shape toward the bigger magnitude eigenvalue

Because exponent on e decays faster, when going the other way the tilt is more gradual

Phase portraits when one of the lamda = 0

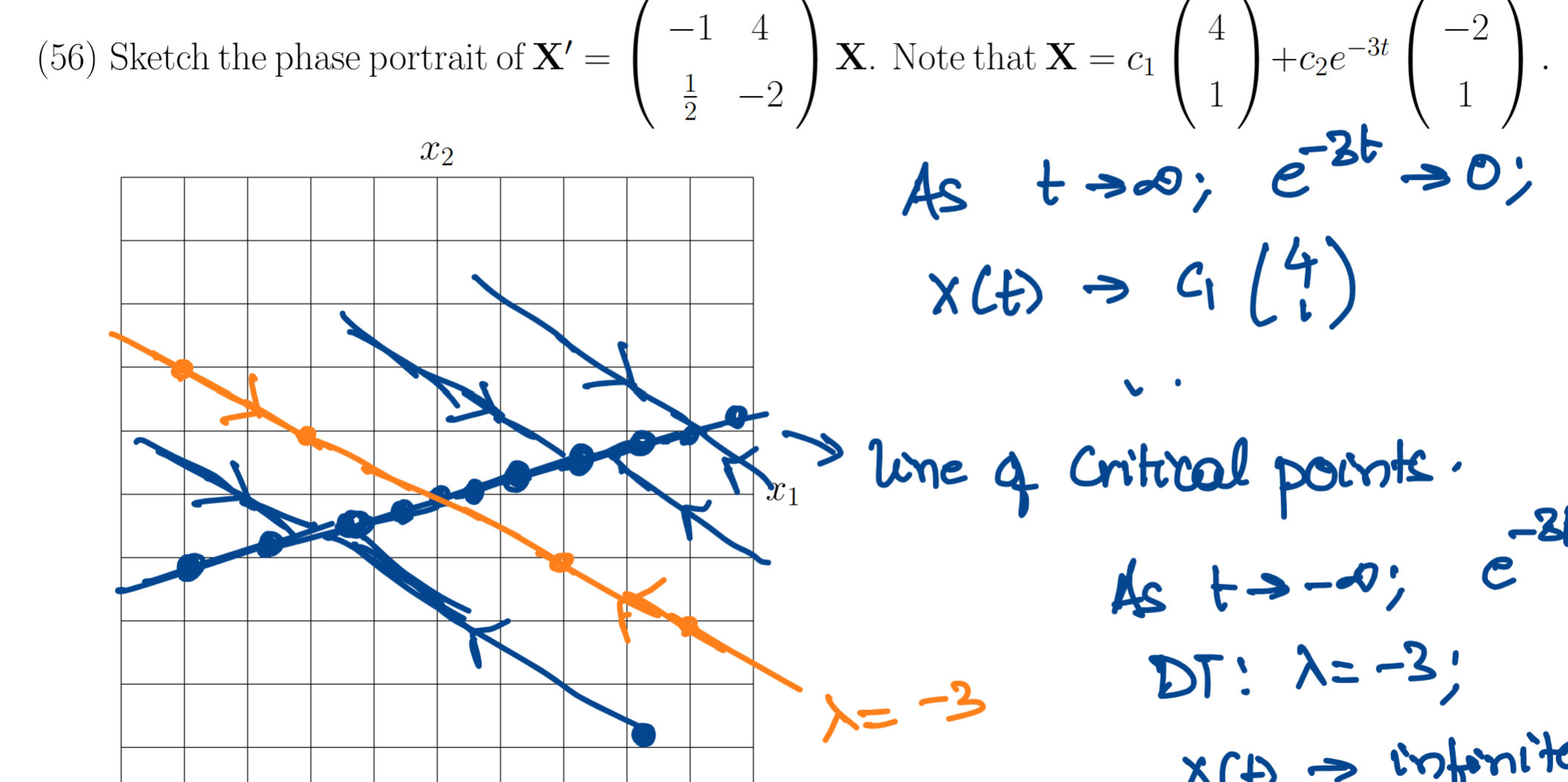
Complex eigenvalue general solution set

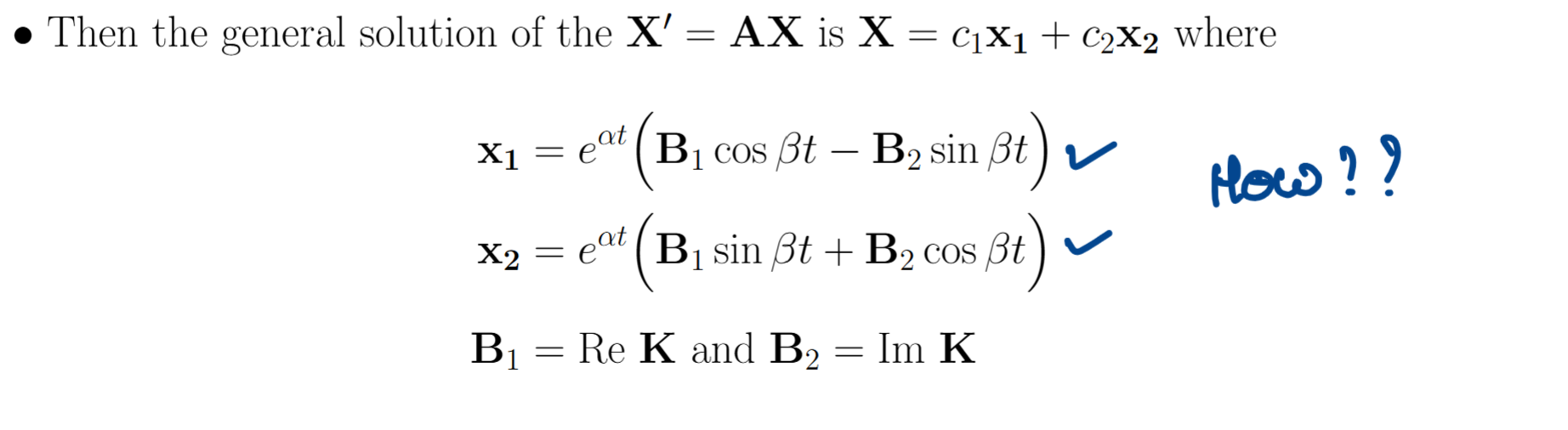
Are complex eigenvectors still the fundamental set of solutions to X’ = AX?

Hell yehhhh they are

Phase portraits for complex eigenvalues

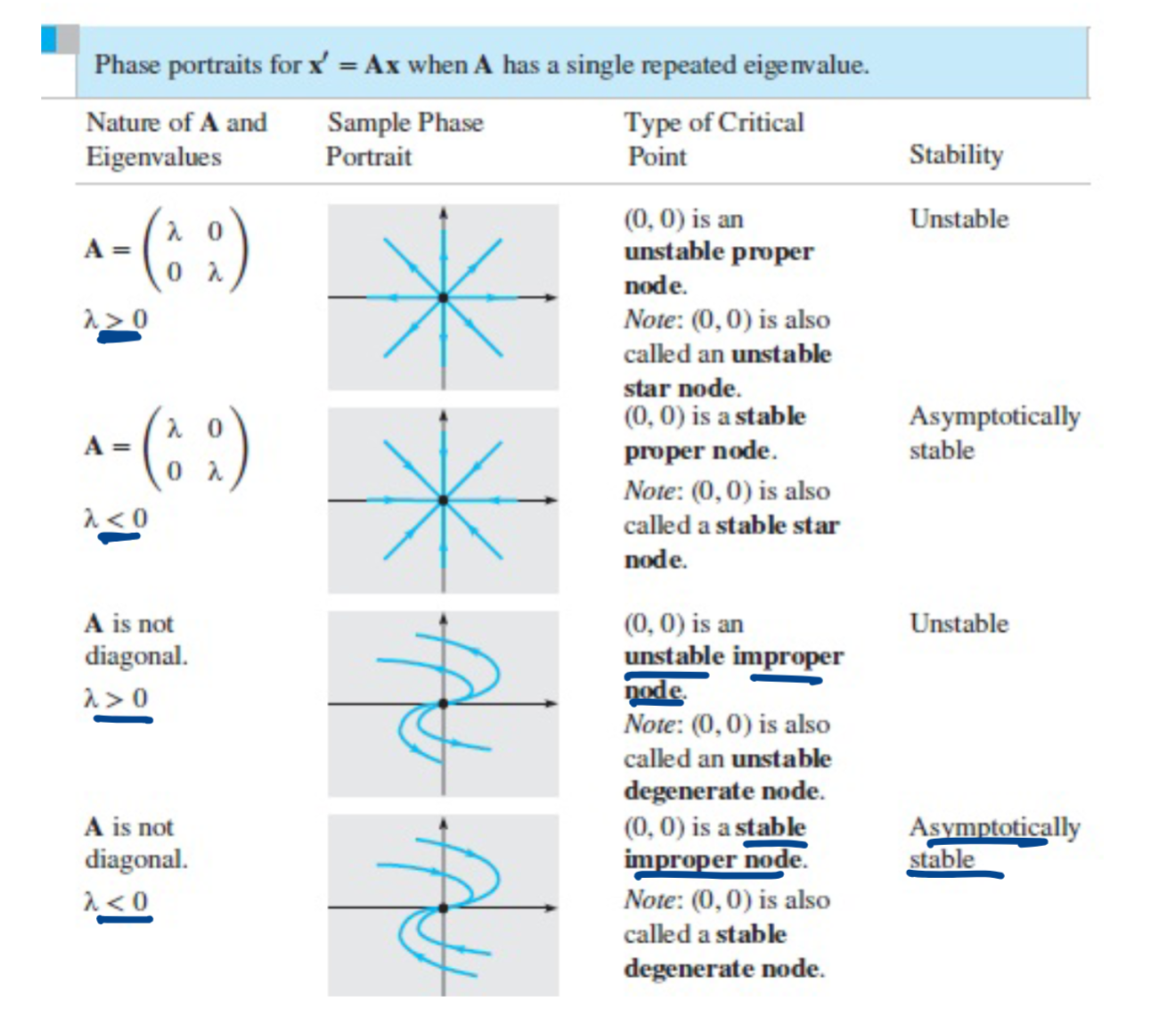
What is the origin called for repeating eigenvalues, two independent eigenvectors

A proper node or star point

Suppose that the matrix A has a repeated eigenvalue (ω) and only one independent eigen-
vector v. Then the origin is called an…

improper or degenerate node

Why does it matter if the soln to a diff eq is stable or not

Phase portraits when A has a single repeated eigenvalue

Difference between alg and geo multiplicities for eigenvalues

For a matrix A, an eigenvalue can have two “multiplicities”:

• Algebraic multiplicity (AM):
  How many times does the lamda appear in characteristic eq (It’s a purely algebraic count.) (if the factor for the eigenvector appears squared, cubed, etc)

• Geometric multiplicity (GM):
  Dimension of the eigenspace for lamda, i.e. how many linearly independent eigenvectors correspond to lamda

Defective matrix

Not enough eigenvectors to diagonalize it

Phase portrait: how to find direction of derivative?

Plug in 1 and 0 for the Cs, see the limit of the solution in that case

Why the weird swirl for double negative eigenvalues?

Because as t decays, the eigenvector component in the bigger vector is removed and it starts to follow the little guy

How to go about graphing the phase portraits without thinking about t

t scales the xs, and the xs determine where the portrait goes

How the professer writes that complex eigenvalue formula

Where B1 is the real component of the eigenvector and B2 is the imaginary component

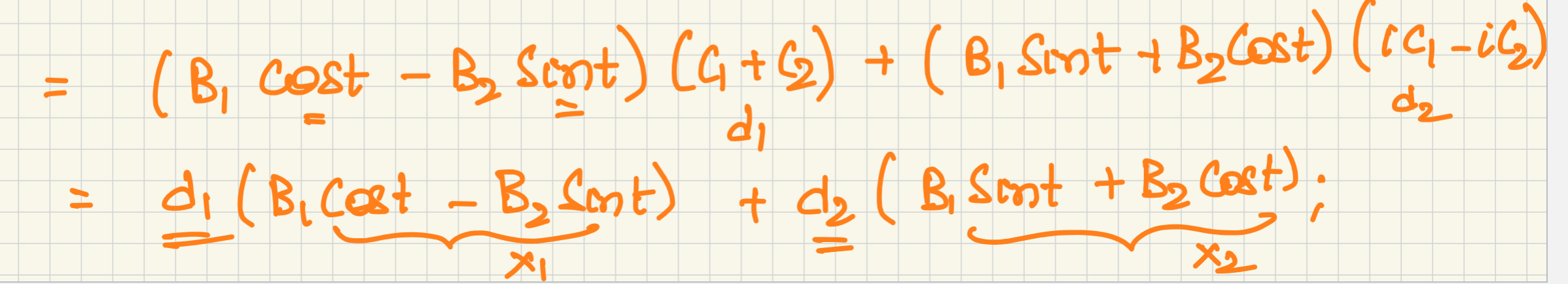
In phase portaits: output for overall x is a…

Vector. So it is dependent on both axises as an output

How is time represented in phase portraits?

In the directionality. The curve is just represented as the posibilities of both xs over the evolution of time

Superposition principle

Abels formula

Wronskian = Ce^integral of P(t)dt, where p(t) is the function in front of the first order term

How many solns does n order diff eq have

n (including trivial solution)

General solns to 2nd order ODE are in the form of…

Exponential functions

General solution to complex eigenvalues: b_im part is…

The COEFFICIENT on the complex part of the eigenvalue, not the actual i itself

Discriminant > 0

2 real and dif eigenvalues

2nd order diff eq with variable coefficients formula MEMORIZE!

After t = lnx substitution

Ables Formula

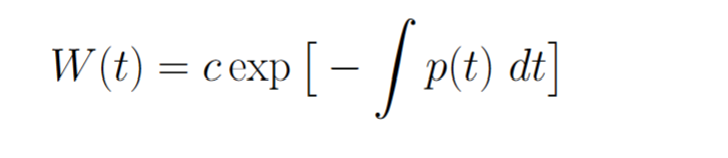
Steps for general soln second order ode homogenous

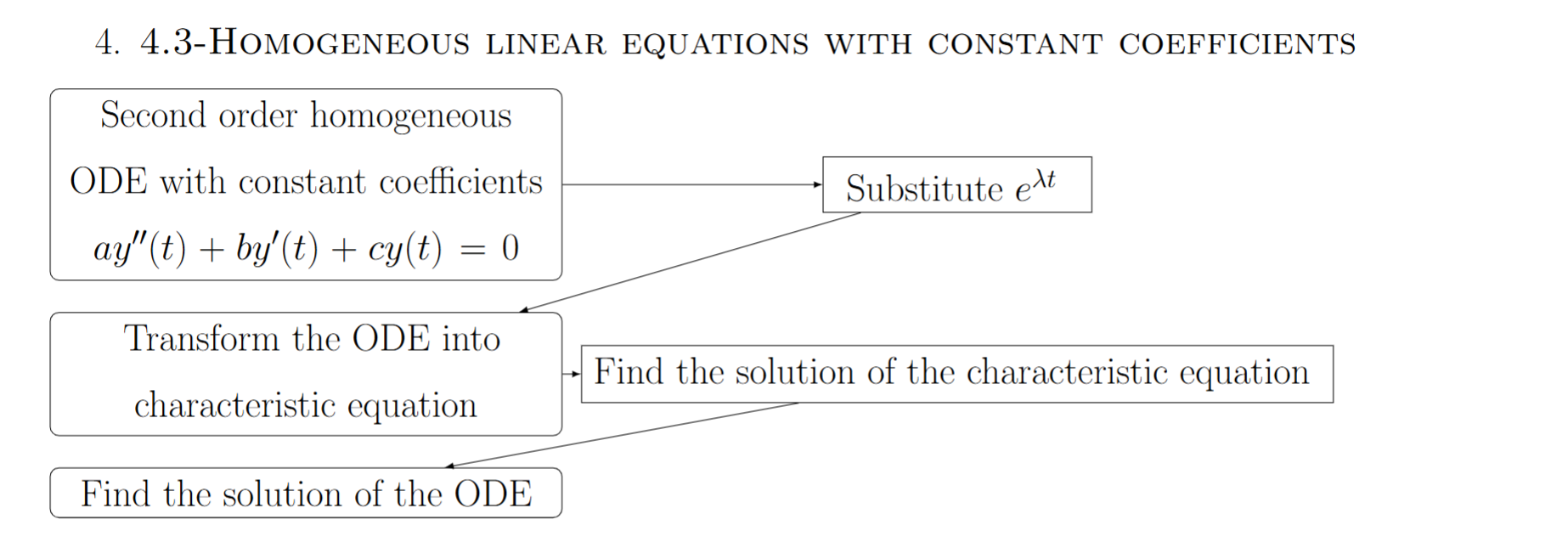
Characteristic equation without matrix

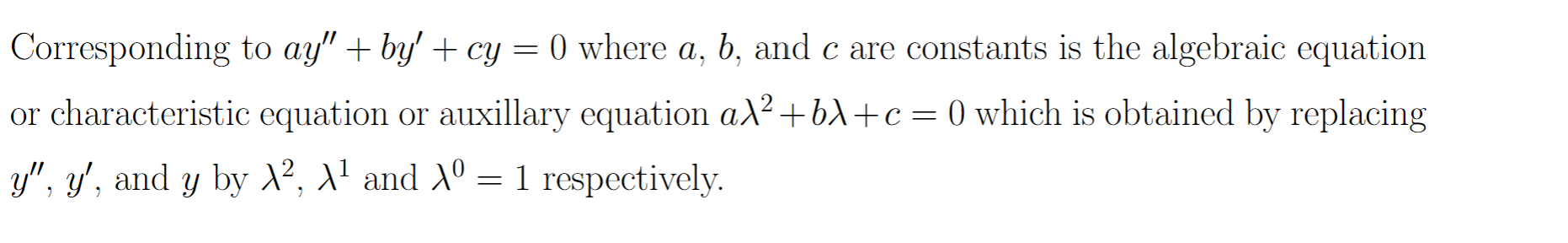
discriminant equals 0 solution to 2nd order ODE

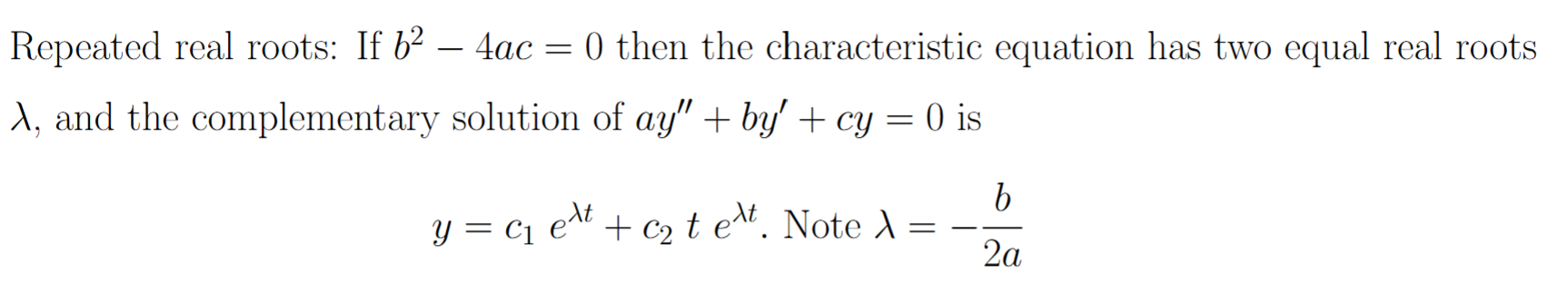
2nd order ODE discrim less than 0 

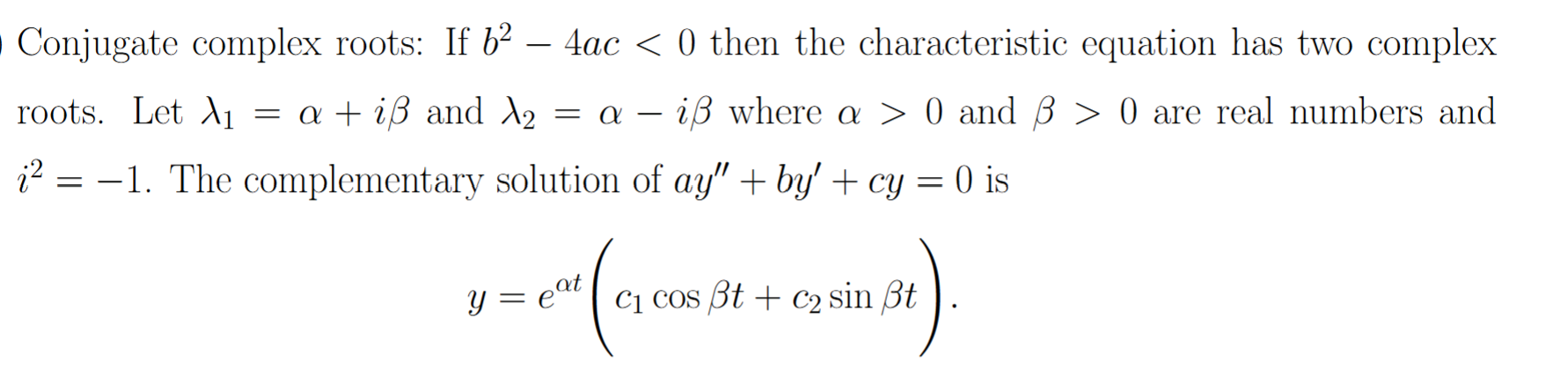
General solution for complex eigenvalues, where p is real component of eigenvector and q is imaginary part

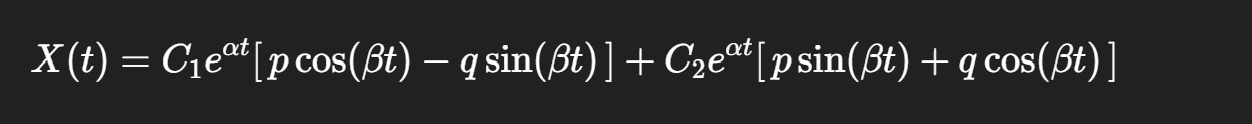
When plotting points of phase portrait: how to plot general solution?

Set one C equal to 1, the other equal to zero so you can see how each component affects the shape

Complex Eigenvalue Formulae split up

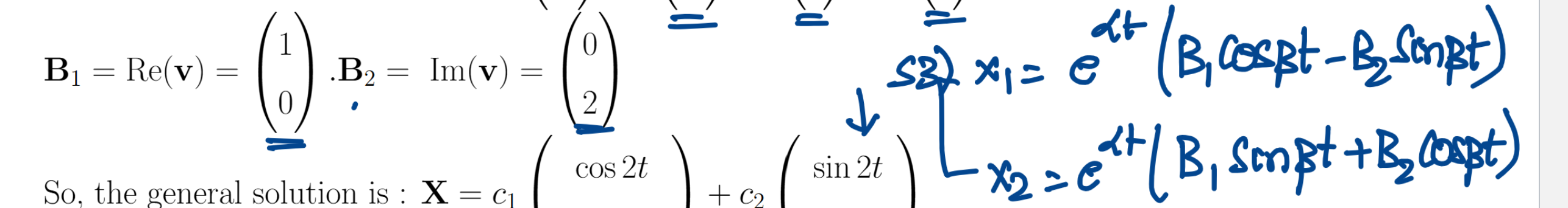
Way to find direction of derivative

Multiply A by X to get derivative

Generalized eigenvector formula (once you have the first, if you’'re looking at double eigenvalue with free variable)

Formula for repeated eigenvalue, incorporating generalized eigenvector (w) while v is the original eigenvector

General process - solving when A is defective and has a repeated eigenvector

Steps for solving defective A

why do improper node phase portraits look how they do

• Improper node case (repeated eigenvalue, only one eigenvector):

  • Only one eigenvector direction exists.

  • First solution: x1(t)=eωtvx_1(t) = e^{\omega t} vx1​(t)=eωtv (trajectories along vvv).

  • Second solution: x2(t)=eωt(tv+w)x_2(t) = e^{\omega t}(tv + w)x2​(t)=eωt(tv+w). Notice the extra ttt term.

• Effect of the ttt factor:

  • The eωte^{\omega t}eωt part makes solutions shrink toward or expand away from the origin (stable if ω<0\omega < 0ω<0, unstable if ω>0\omega > 0ω>0).

  • The extra tvt vtv part “pulls” trajectories gradually toward the eigenvector direction.

• Resulting geometry in the plane:

  • The only true straight-line trajectories are along the eigenvector.

  • All other trajectories curve toward that line as t→∞t\to\inftyt→∞ (if stable) or as they move away (if unstable).

  • That’s why the picture looks like a funnel or sheaf of curves bending into (or away from) one main direction.

phase portraits repeated eigenvalues

When solving for the generalized eigenvector, do not…

Row reduce! The expression on the left is set equal to the eigenvector, not zero

how to draw an improper node phase portrait

1. Draw eigenvector

2. Test (0, 1) and (1, 0). Plugging these in will give you derivative, which tells you where it points, and you trace that to the origin.

Once you get y for a shifted system…

Write general solution to regular Q, then substitute Y into the general solution expression, and solve for any initial values

Just want you to see general solution both with and without c

When have the spiraling complex to graph:

Just plug in points around it even if its not through the same curve