Lecture 4: Antagonists in Functional Assays

Antagonism

• A situation where adding two drugs into a system produces a lower response than would be expected in the drugs were added individually.

Simple Competitive Antagonists

• When the agonist binds response occurs; when the antagonist binds (to the same site as the agonist) no response is seen

Functional Antagonism

• Agonist binding results in a positive response; Agonist binding results in a negative response; responses from A and B cancel each other out

Non-Competitive Antagonists

• Agonist binds and response occurs; agonist and antagonist bind (to separate binding site) and no response occurs

Indirect Antagonism

• Drug acting on a target causes the release of a transmitter that acts on receptor 1 to release a transmitter to activate receptor 2; when an antagonist is bound no response is seen as it blocks the actions of drug 1

Competitive Antagonist

• Occurs when an antagonist binds to the same site as an agonist

• It is an important mechanism from a therapeutic perspective, with many drugs acting at receptors through this mechanism

Gaddum Eqaution

• Used to deal with competitive binding

• Binding of a drug (D) is measured in the presence of a competing ligand, I.

• Kd is the affinity of D,

• Ki is the affinity of I

• Bmax is the maximum binding the system can produce

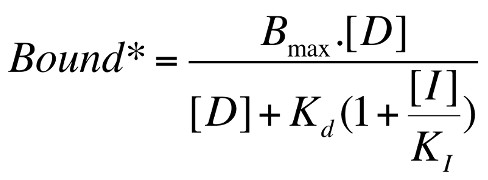
Gaddum Equation for Functional Measurements

• Change B for binding into E for effect, and swap Ki for EC50

•  [D] is the concentration of the agonist,

• [I] is the concentration of the competitive antagonist

• K_I is the equilbrium dissociation constant for the antagonist (i.e. the antagonist's K_d value).

Measurements From Inhibition Assays

• Use the Gaddum equation to study competition binding.

• A fixed concentration of radiolabeled ligand is displaced by varying concentrations of a competing ligand.

• This gives an IC₅₀: concentration of competitor that displaces 50% of the labelled ligand.

• IC₅₀ depends on:

  • The concentration [D] and affinity (Kᴅ) of the radioligand.

• The Cheng-Prusoff equation converts IC₅₀ to Kᵢ (true affinity of the competitor)

Calculation of IC50

1. Normalise data to the control response (% of control).

2. Plot log(inhibitor) vs response and fit data using a 3-parameter inhibition equation (e.g., in Prism).

3. This yields an IC₅₀ (e.g., 2 nM).

4. Use a modified Cheng-Prusoff equation for functional assays:

   Ki=IC501+[D]EC50Ki​=1+EC50​[D]​IC50​​

Limitations of Method Used to Calculate IC50

• Assumes competitive antagonism.

• May not be valid with agonists showing cooperativity.

• Assumes EC₅₀ ≈ Kᴅ, which may not always hold.

Difficulties in Applying Cheng Prusoff Equation

• Assumes EC₅₀ = Kᴅ, which is rarely true in practice.

• Assumes non-cooperative binding of the agonist.

• Only valid for competitive antagonism—does not confirm that antagonism is competitive.

• A more accurate method for functional data is Schild analysis, which specifically analyzes competitive antagonists.

Characeteristics of Competitive Antagonism

• No change in Emax (maximum response remains the same).

• Parallel rightward shift in the concentration-response curve.

• Apparent increase in EC₅₀, now called EC₅₀* in the presence of an antagonist.

• EC₅₀* increases in direct proportion to antagonist concentration [I].

• This behaviour is described using the Gaddum equation.

Schild equation

• CR=1+[I]Ki

  where CR = concentration ratio = EC50*/EC50

• Derived by rearranging the Gaddum equation.

• CR removes agonist-related variables (like EC₅₀ vs Kᴅ differences).

• Makes analysis more reliable—agonist variability cancels out.

• Developed by Heinz Otto Schild.

Rearranged Schilds Equation

• Log(CR-1) = log[I]-LogK1

• CR=1+([I]/Ki); CR-1=[I]/Ki.

  • Now take logs: when taking logs, division becomes subtraction, so: log(CR-1) = log[i]-log Ki

• This form of the equation allows for Log(CR-1) to be plotted against log {i{ and gives a linera graph with a slop of 1 and the y-axis intercept equal to -logkI

What Does Schilds Plot Reveal About Antagonism

• Schild plot: log(CR − 1) vs log[Antagonist].

• A straight line with slope = 1 suggests competitive antagonism.

• If the line is not straight or the slope ≠ 1, the antagonism is not competitive.

• Caution: Some non-competitive antagonists can also produce a slope ≈ 1 — additional tests may be needed.

How Does the Schild Plot Provide Information About Antagonist Potency

• Y-axis intercept of the Schild plot = log(Kᵢ) → gives antagonist affinity.

  • From log(Kᵢ), calculate Kᵢ (dissociation constant).

• X-axis intercept = when log(CR − 1) = 0, i.e. CR = 2, meaning the antagonist has doubled the apparent EC₅₀.

  • intercept gives a point of antagonist potency (where [I] causes a 2-fold shift in EC₅₀).

  • antagonist concentration at this point = measure of potency.

  • This value is expressed as a negative log concentration, called pA₂.

  • pA₂ = −log[antagonist] that gives CR = 2.

• Plot must be linear for the interpretation to be valid.

pA2

• "The negative logarithm to base 10 of the molar concentration of an antagonist that makes it necessary to double the concentration of the agonist needed to elicit the original submaximal response obtained in the absence of antagonist"

EC50

• a "sub-maximal concentration" - pA₂ in considered as the apparent EC₅₀ value doubling

Relationship Between pA2 and Ki

• For a perfect competitive antagonist, the log K_i value can be obtained either from the x or y intercepts:

  • x intercept (y = 0)

  • 0 = log[I]-logKi

  • logKi = log [I]

  • y intercept (x=0)

  • log (CR-1) = -logKi

• Therefore, if we have competitive antagonism, pA₂ = -log K_i. Note, however, that this is not the definition of pA₂.

F-Test

• Compares two models:

  1. Fixed slope = 1 (y = x + c)

  2. Variable slope (y = mx + c)

• Tests whether the more complex (variable slope) model fits significantly better.

• If p < 0.05 → variable slope improves fit → not competitive antagonism.

• If p > 0.05 → no significant improvement → use simpler model (slope = 1) → competitive antagonism likely.

• Helps confirm the mechanism of antagonism

How Do 95% confidence intervals help in examining the slope in Schild plot analysis?

• 95% CI: Range of values where you can be 95% certain that the true slope lies'/ 5% chance that the true slope lies outside this range

• If the 95% CI includes 1 (e.g. 0.7 to 1.1), competitive antagonism cannot be ruled out.

• If the 95% CI does not include 1 (e.g. 0.7 to 0.9), competitive antagonism can be rejected with <5% chance of being true.

• Helps determine if the data supports competitive antagonism or another mechanism.

Importance of pA2

• High values indicates an antagonist of high potency and can indicate high specific of the antagonism

  • e.g., atropine blocks ACh receptors with low potency at histamine receptors

• Similar values across different tissues suggest similar receptors in those tissues, better than comparing EC50 values, which can be affected by spare receptors.

• Identical values for different agonists suggest they act on the same receptor, helping confirm receptor specificity.