Handout 3: Expected value, variance, standard deiviation

Week 3

What is a random variable?

A way to denote that what happens is up to chance

• Discrete (finite number of outcomes)

• Continuous (infinite number of outcomes)

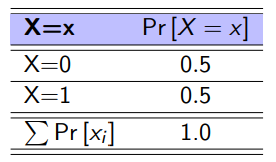
What is the probability model?

Consists of:

1. The possibilities (the values that a random variable could take on)

2. The probabilities of each occurring

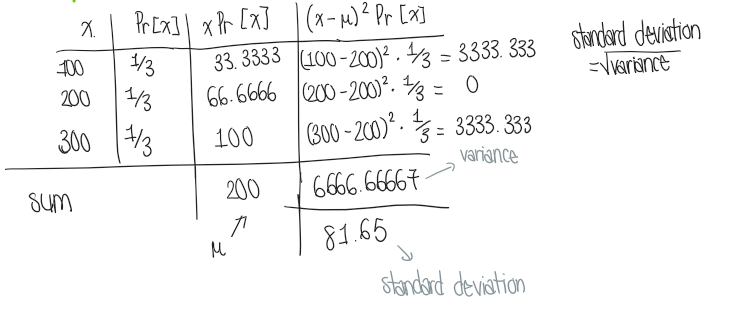
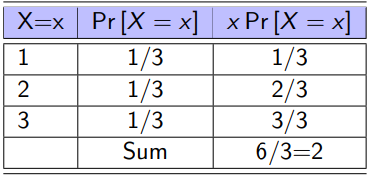
What is expected value E[X]?

The typical result

In a table, the expected values mean nothing individually, but mean something when added up

• Possibilities x Probabilities

What is variance?

The measure of spread/risk → how much variation in outcome is expected

• always positive

• = ( x - expected value)² x Pr(x)

• Variance = Standard deviation²

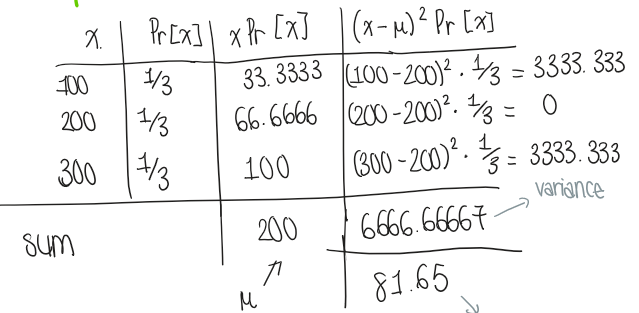
What is standard deviation?

shows how spread out or clustered the data points are

• Standard deviation = √variance