Geometry Final Study Guide - Sophomore Year

TOPIC 5.1 CLASSIFYING TRIANGLES

TOPIC 5.1 CLASSIFYING TRIANGLES

Triangles are classified by…

angles and sides

we name a triangle with the…

angle first and the sides second

Classifying by angles

Classifying by angles

Acute Triangle

3 acute angles

all angles measure <90 degrees

Equiangular Triangle

3 congruent angles

all angles have equal measure

Obtuse Triangle

1 obtuse angle

one angle measures >90 degrees

Right Triangle

1 right angle

one angle measure 90 degrees

Classifying by sides

Classifying by sides

Equilateral Triangle

3 congruent sides

all sides have equal measure

Isosceles Triangle

2 congruent sides

at least 2 sides have equal measure

Scalene triangle

0 congruent sides

no sides have equal measure

Proving triangle interior angles = 180

Proving triangle interior angles = 180

angles A, B, and C add up to…

180 degrees

<A + <B + <C = 180 degrees

Finding missing interior angles

Finding missing interior angles

example 1

70 + 35 + a = 180

70 + 35 = 105

180 - 105 = 75

a = 75

Acute Scalene

example 2

117 + 17 + a = 180

117 + 17 = 134

180 - 134 = 46

a = 46

Obtuse Scalene

see special example in notebook

35 + 35 + 40 = 110

35 + 110 + 5b = 180

145 + 5b = 180

-145 on both sides

5b = 35

divided by 5 on both sides

b = 7

Exterior Angles Theorem

Exterior Angles Theorem

the exterior angle of a triangle is…

always equal to the sum of the two opposite interior angles of a triangle

<d = <a + <c

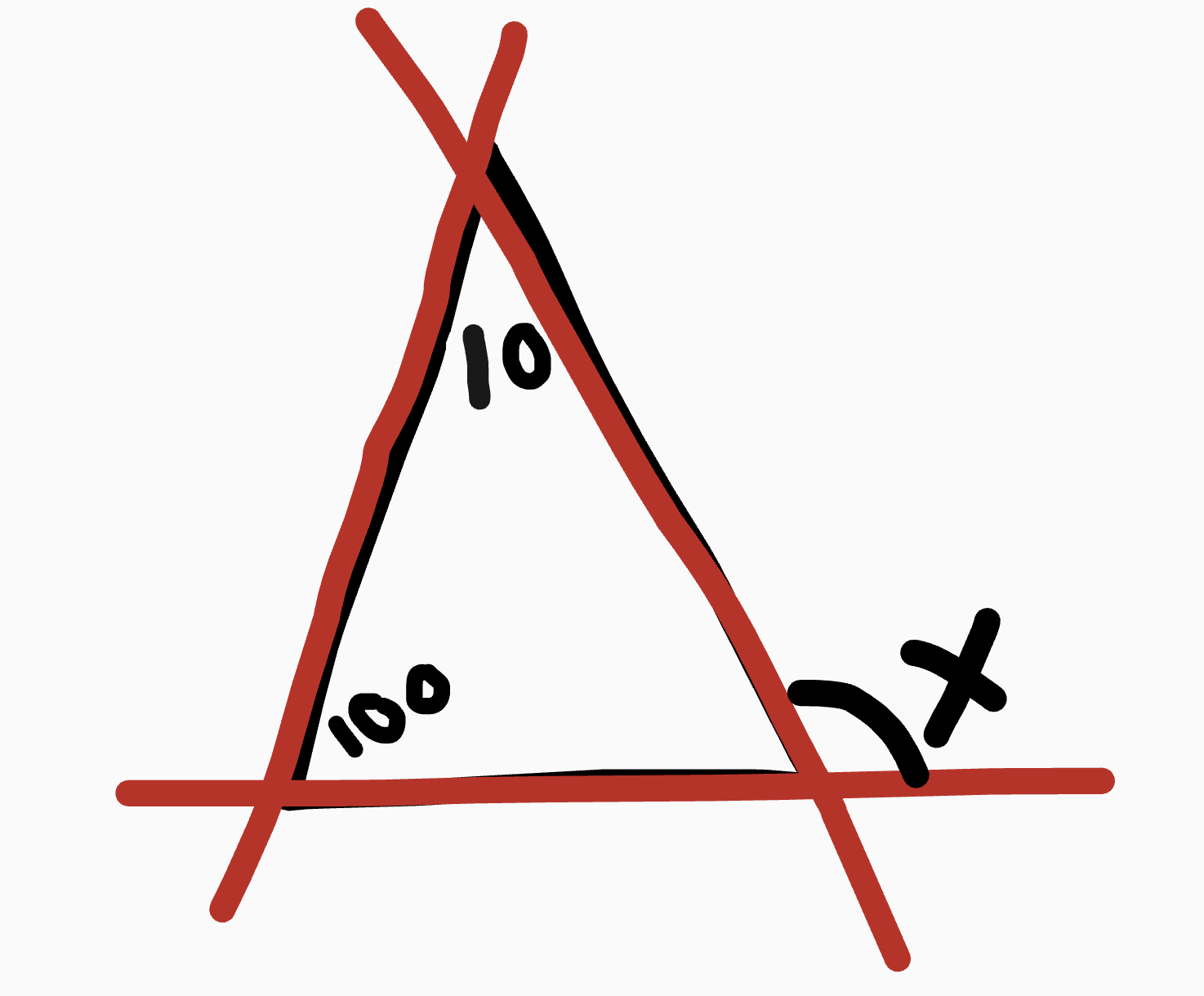
Finding missing exterior angles

Finding missing exterior angles

example

x = 110

TOPIC 5.2

TOPIC 5.2

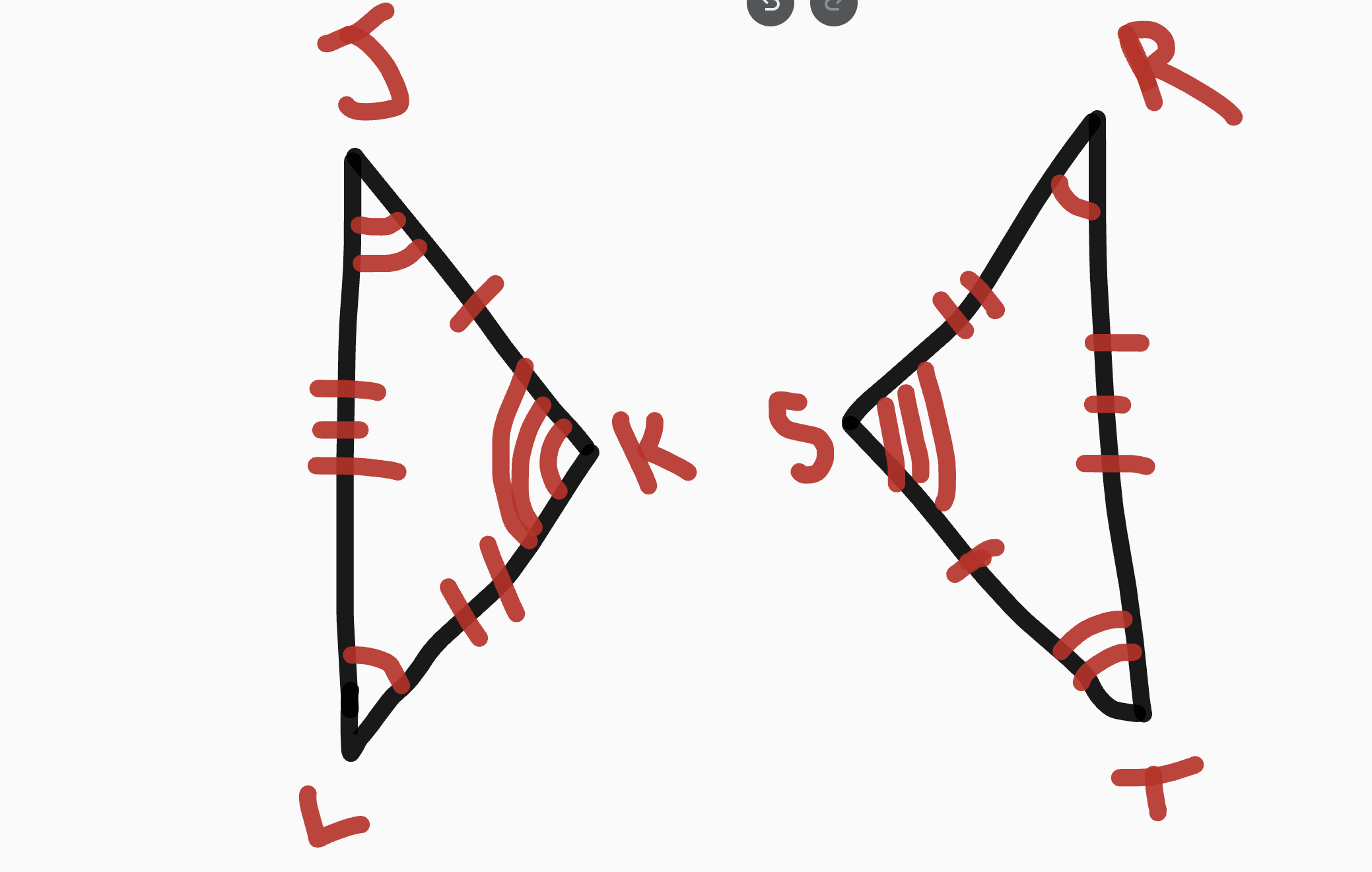
Identifying Corresponding Parts

Identifying Corresponding Parts

< L =

<J =

<K =

Side JK =

Side KL =

Side LJ =

<R

<T

<S

Side TS

Side SR

Side RT

to show congruency, the sign is and equal sign with a squiggle on top of it

to show congruence in sides, put a line over the top of the letters of the sides

Corresponding Parts and Congruence Statements

Corresponding Parts and Congruence Statements

triangle ABC is congruent to triangle XYZ

Topic 5.3

Topic 5.3

How can triangles be congruent?

Triangles can be proven congruent by SSS, ASA, SAS, AAS and HL- never AAA or SSA

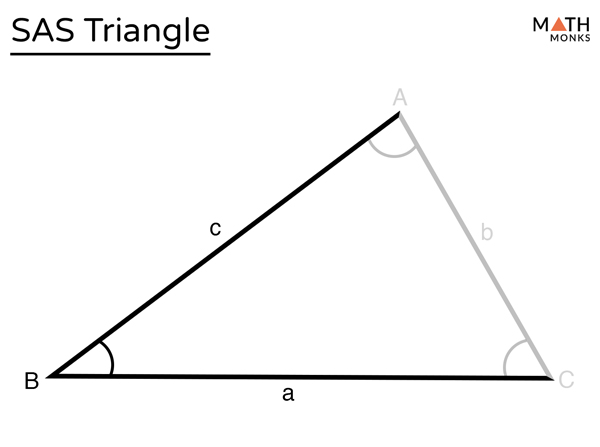
SAS - Side Angle Side

Two sides and the included angle are congruent

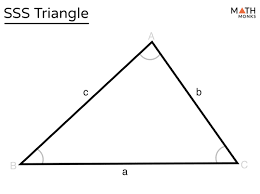
SSS - Side Side Side

all 3 sides are congruent

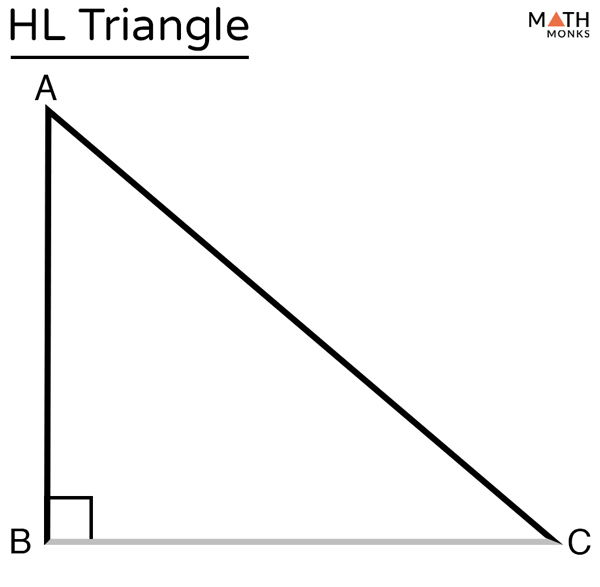
HL (right triangles only) - Hypotenuse- Leg

The Hypotenuse and one of the legs are congruent

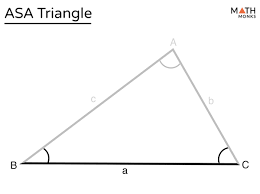
ASA - Angle Side Angle

Two angles and the included side are congruent

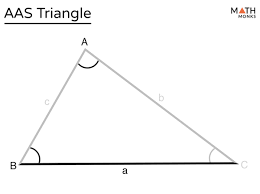
AAS - angle angle side

2 angles and a non-included side are congruent

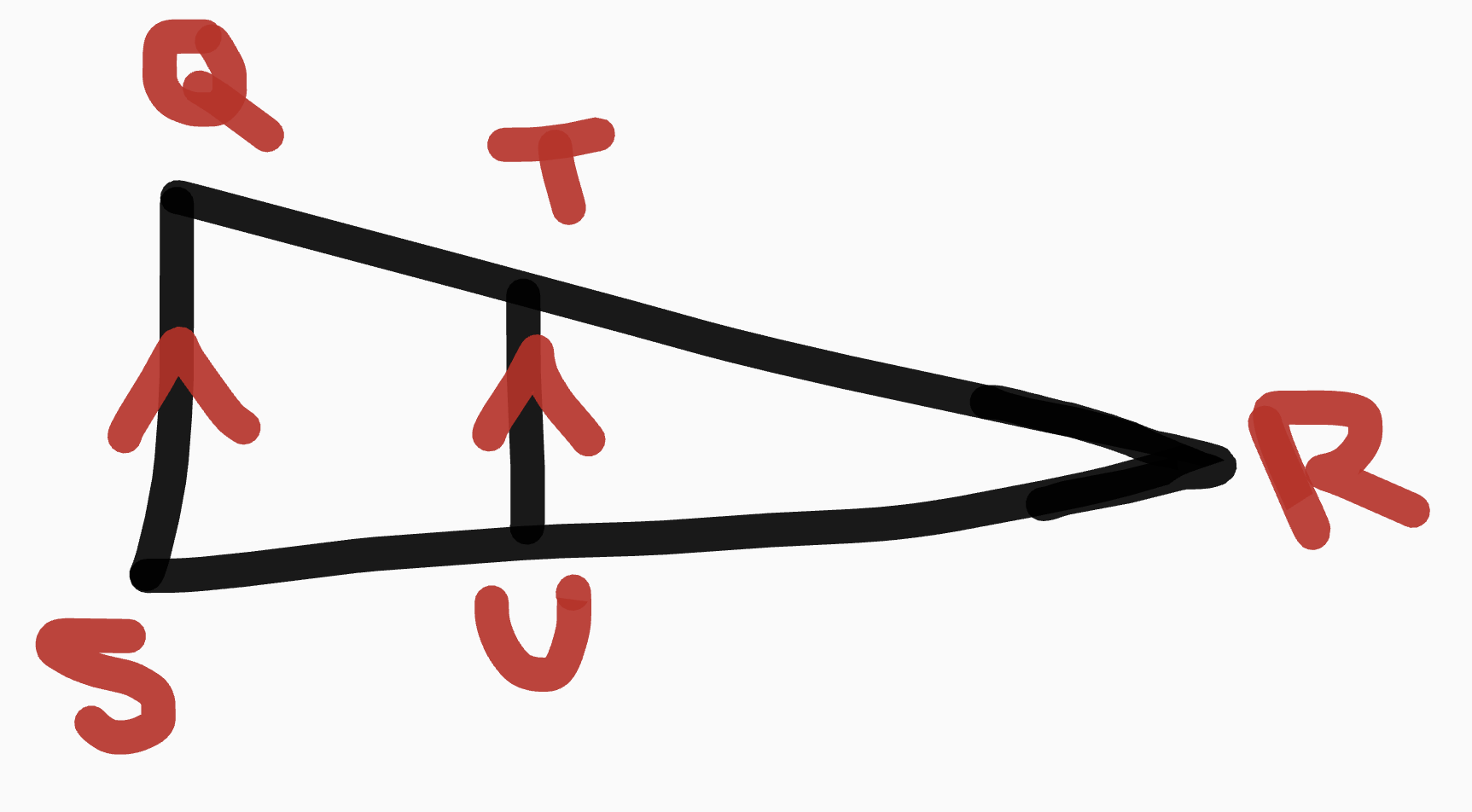
Side-Side-Side Congruence

if 3 sides of a triangle are congruent, then the triangles are congruent

Topic 6.4 - Triangle Midsegment Theorem

Topic 6.4 - Triangle Midsegment Theorem

Definition of a midsegment

the line segment that extends between the midpoints of any 2 sides of a triangle

To find the base of a triangle…

multiply the midsegment by 2

to find the midsegment of a triangle…

divided the base by 2

Solving side length…

each piece of side length is congruent

• If you are given the whole length, divide by 2

• If you are given 1 piece, the 2 parts are equal

Topic 8.4 - Proportions in triangles

Topic 8.4 - Proportions in triangles

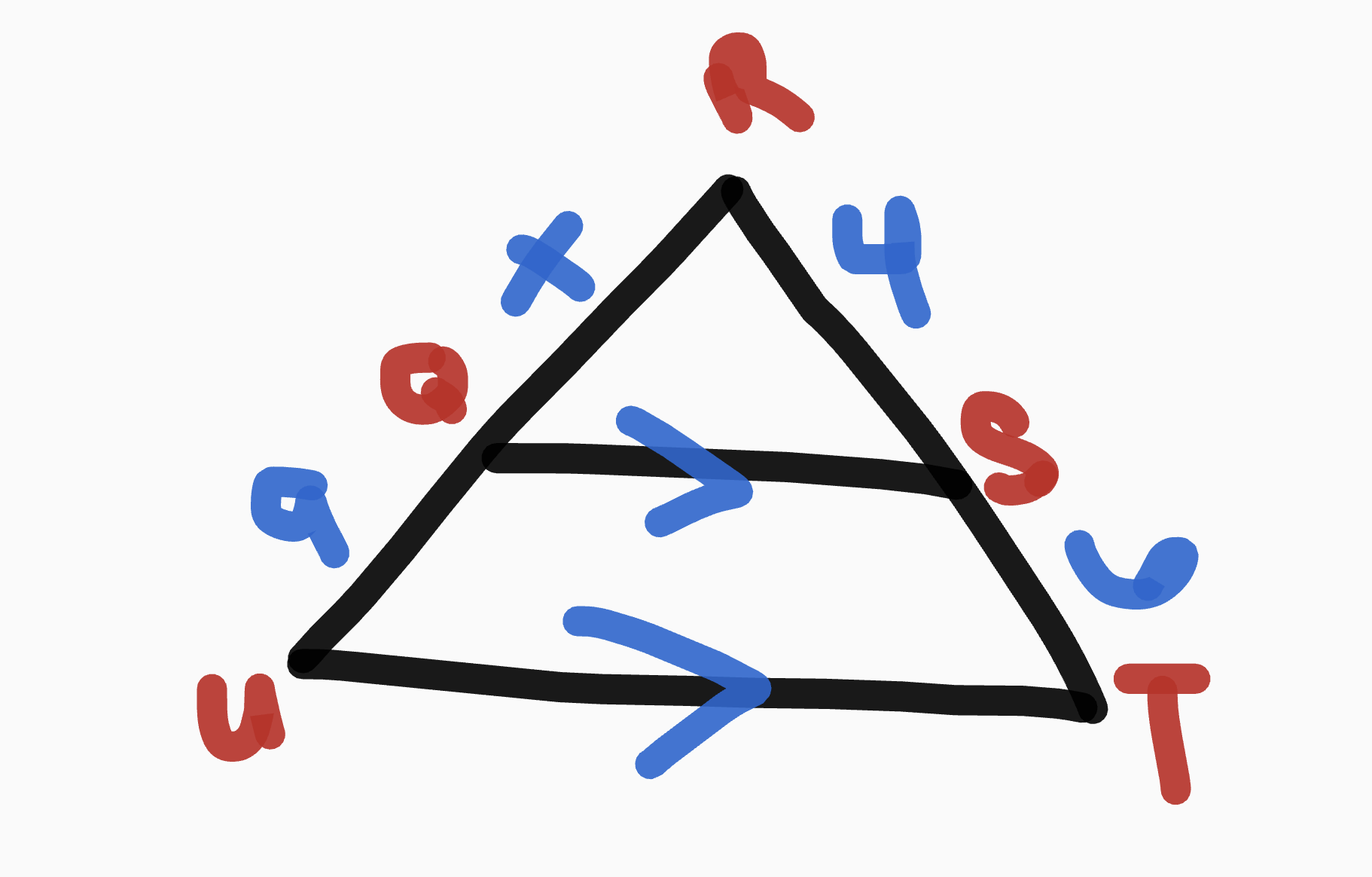
Triangle Proportionality Theorem

AKA: The Side Splitter

If a line is parallel to one side of the triangle and intersects the 2 other sides, then the sides are split proportionally

example 1

If TU is parallel to QS, then RT/TQ = RU/US

example 2

4/6 = x/9

x = 6

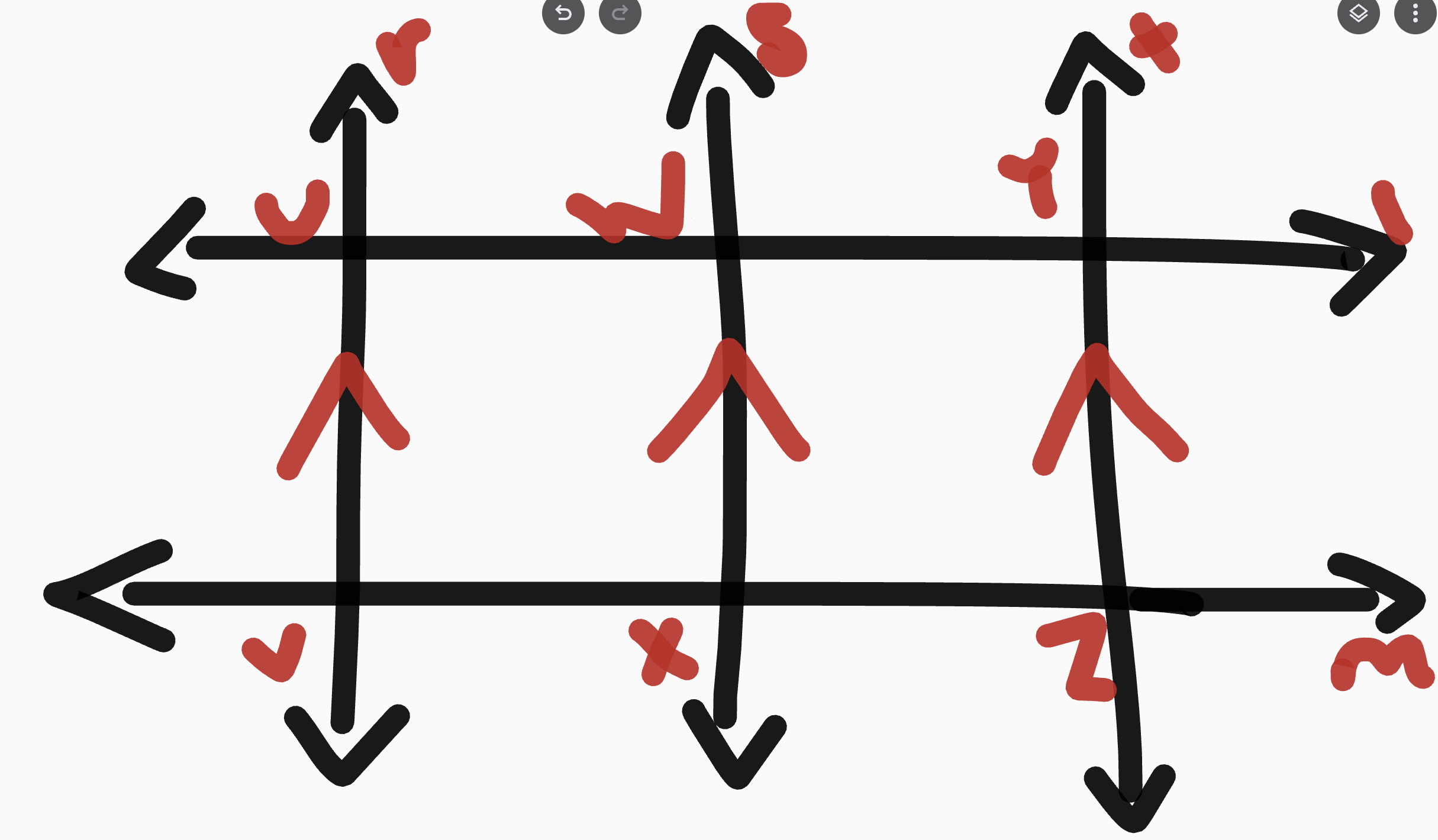
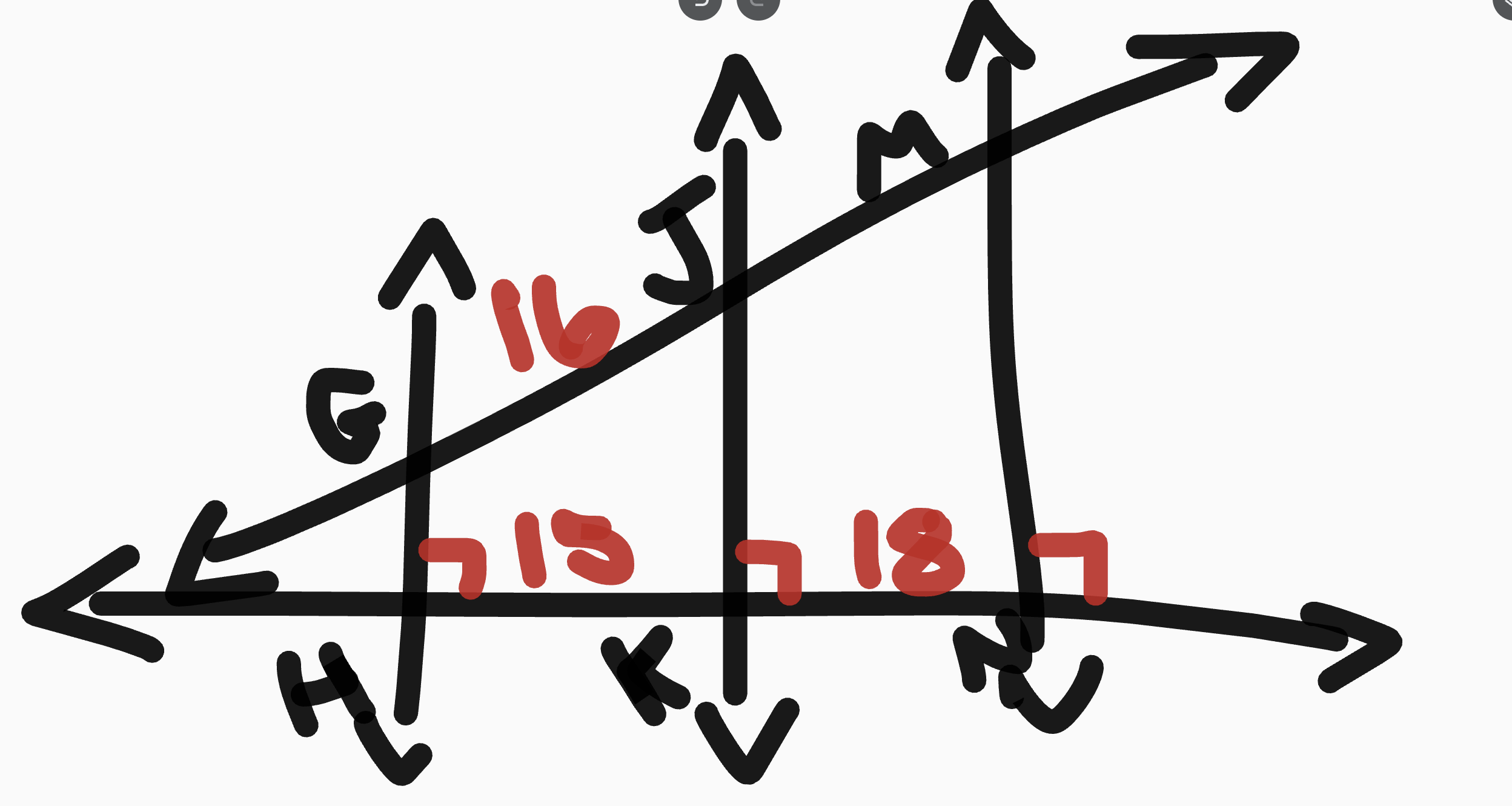
Three Parallel lines Theorem

If 3 parallel lines intersect 2 transversals, then they divide the transversals proportionally

example 1

UW/WY = VX/XZ

example 2

16/x = 15/18

x = 19.2

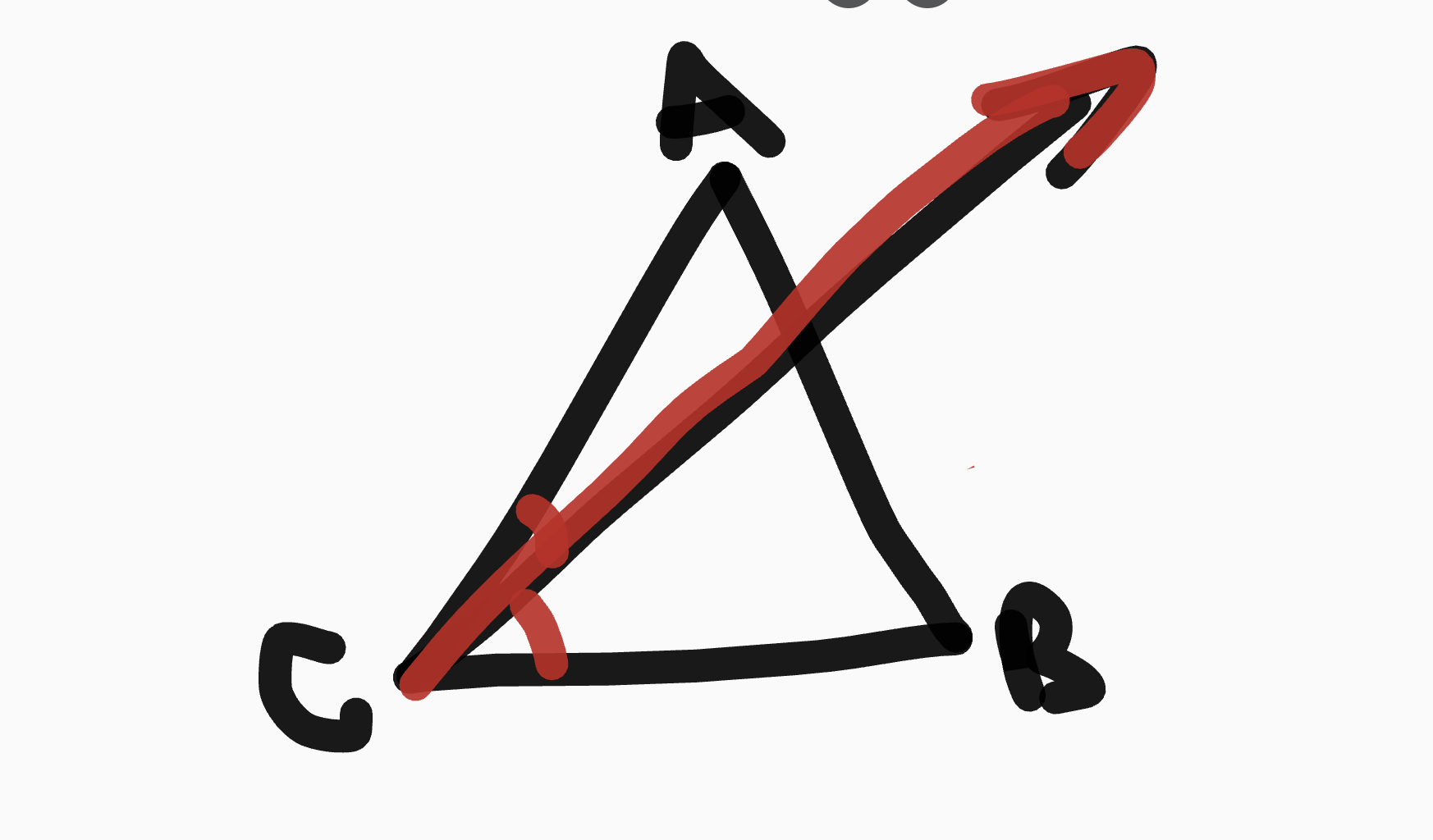
Triangle Angle Bisector Theorem

If a segment (ray, line) bisects an angle of a triangle, then it divides the opposite side into lengths that are proportional to the other 2 sides

example 1

AD/DB = CA/CB

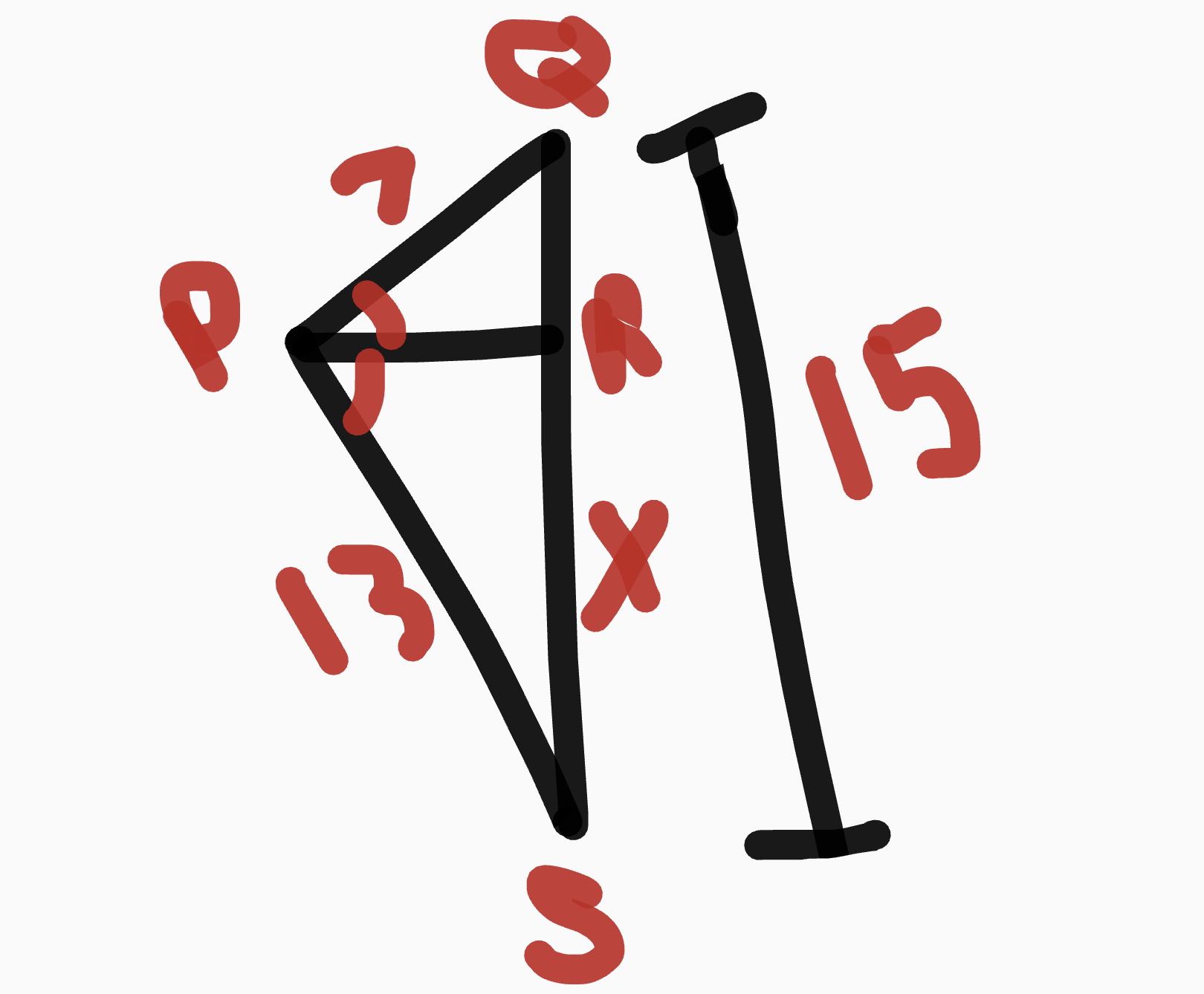
example 2

15 - x/x = 7/13

x = 9.75 or 9.8

TOPIC 9.1 - The Pythagorean Theorem

TOPIC 9.1 - The Pythagorean Theorem

Vocab

Leg

Hypotenuse

Pythagorean Theorem

leg

one of the 2 short sides of a triangle

ex: sides A and B

Hypotenuse

the largest side of a right triangle the side across from the 90 degree angle

ex: side C

Pythagorean Theorem

When all 3 sides are all perfect whole numbers

ex:

3 × 4 × 5

6 × 8 × 10

Steps for Pythagorean Theorem:

1) Label sides a,b,c

2) Write formula a² + b² = c²

3) substitute a,b, and c

4) solve each equation

Topic 9.2 - Special Right Triangles

Topic 9.2 - Special Right Triangles

Special Right Triangle Rules

45-45-90

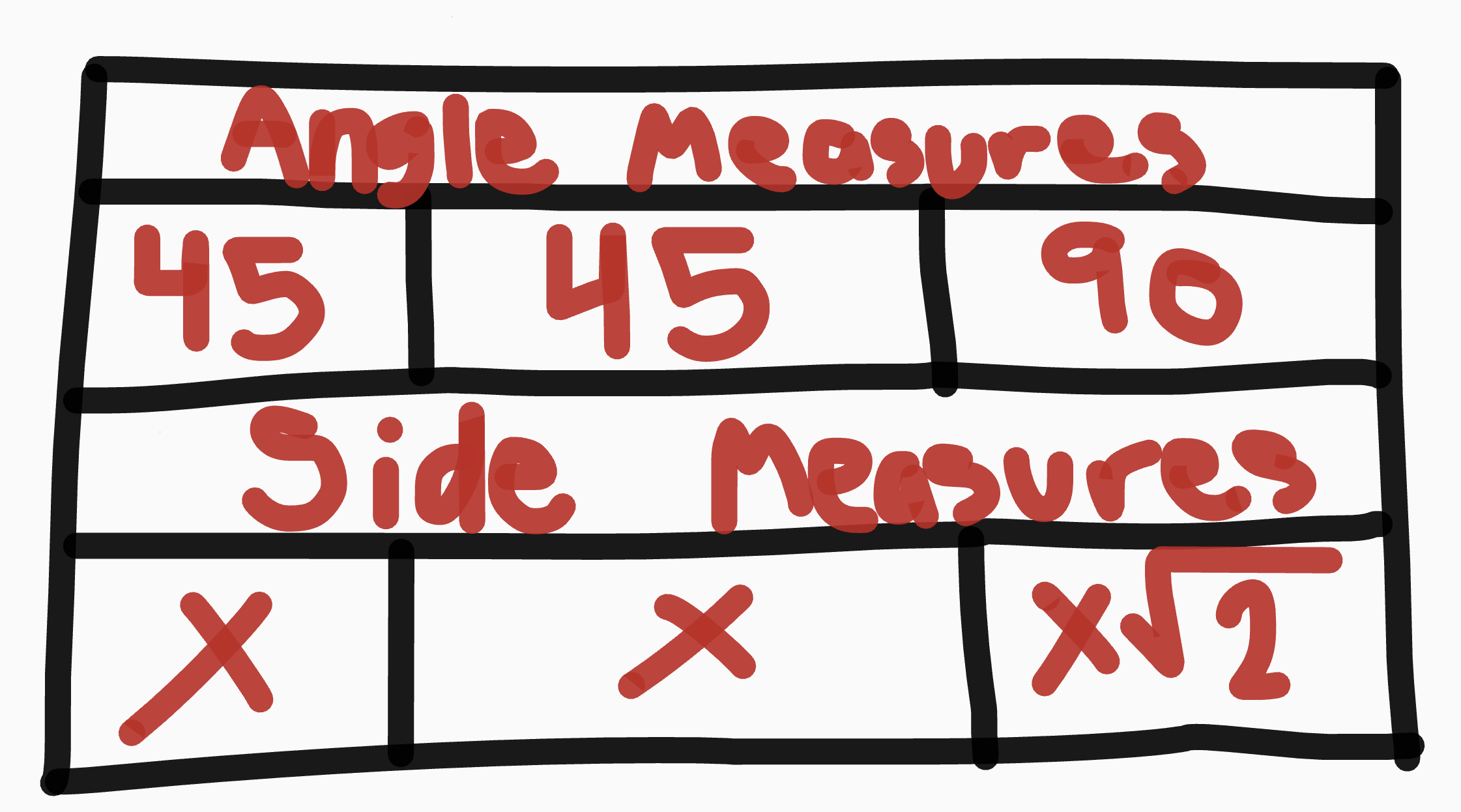
½ of a square

Right Isosceles triangle

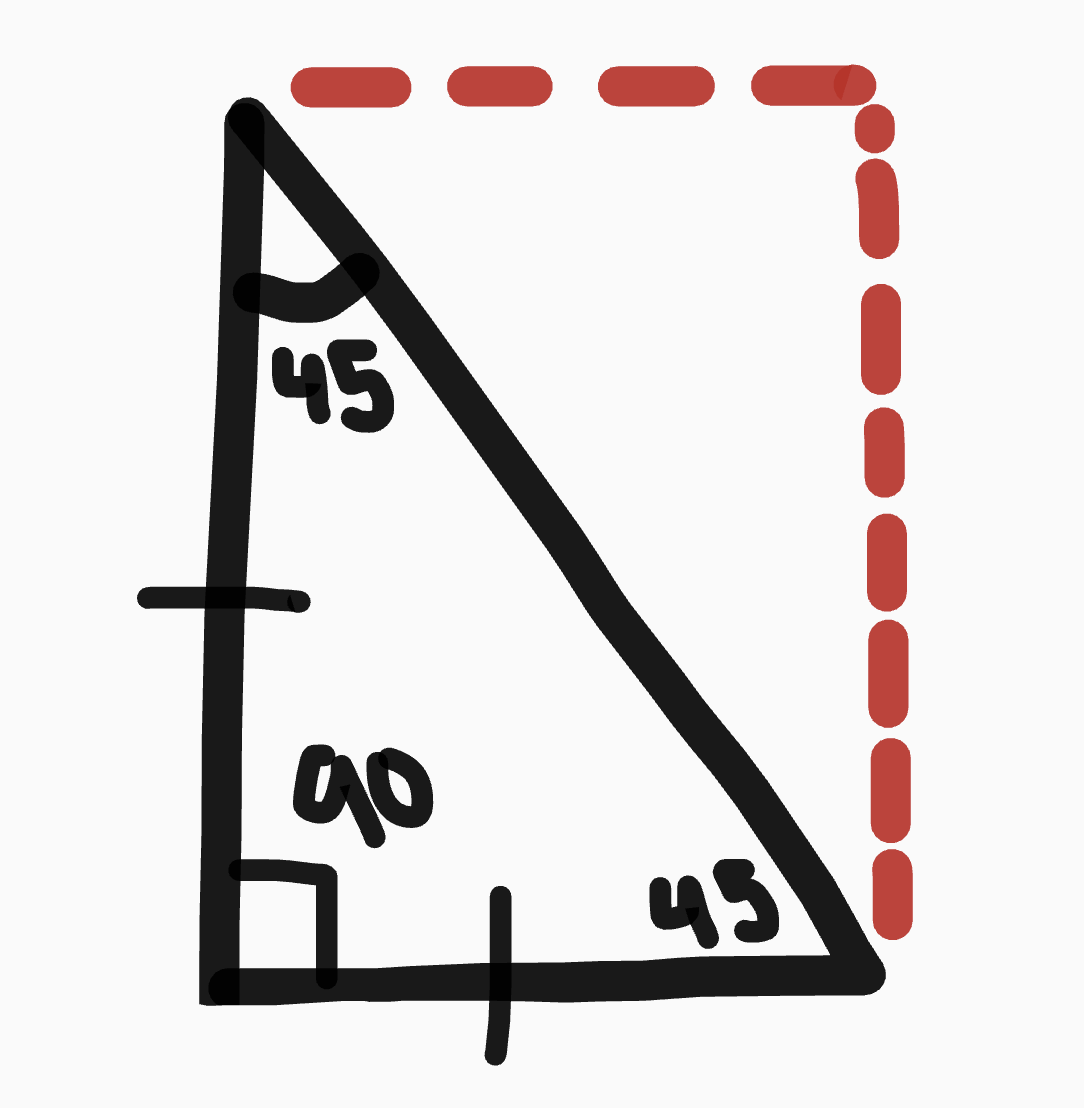
Special Right Triangle

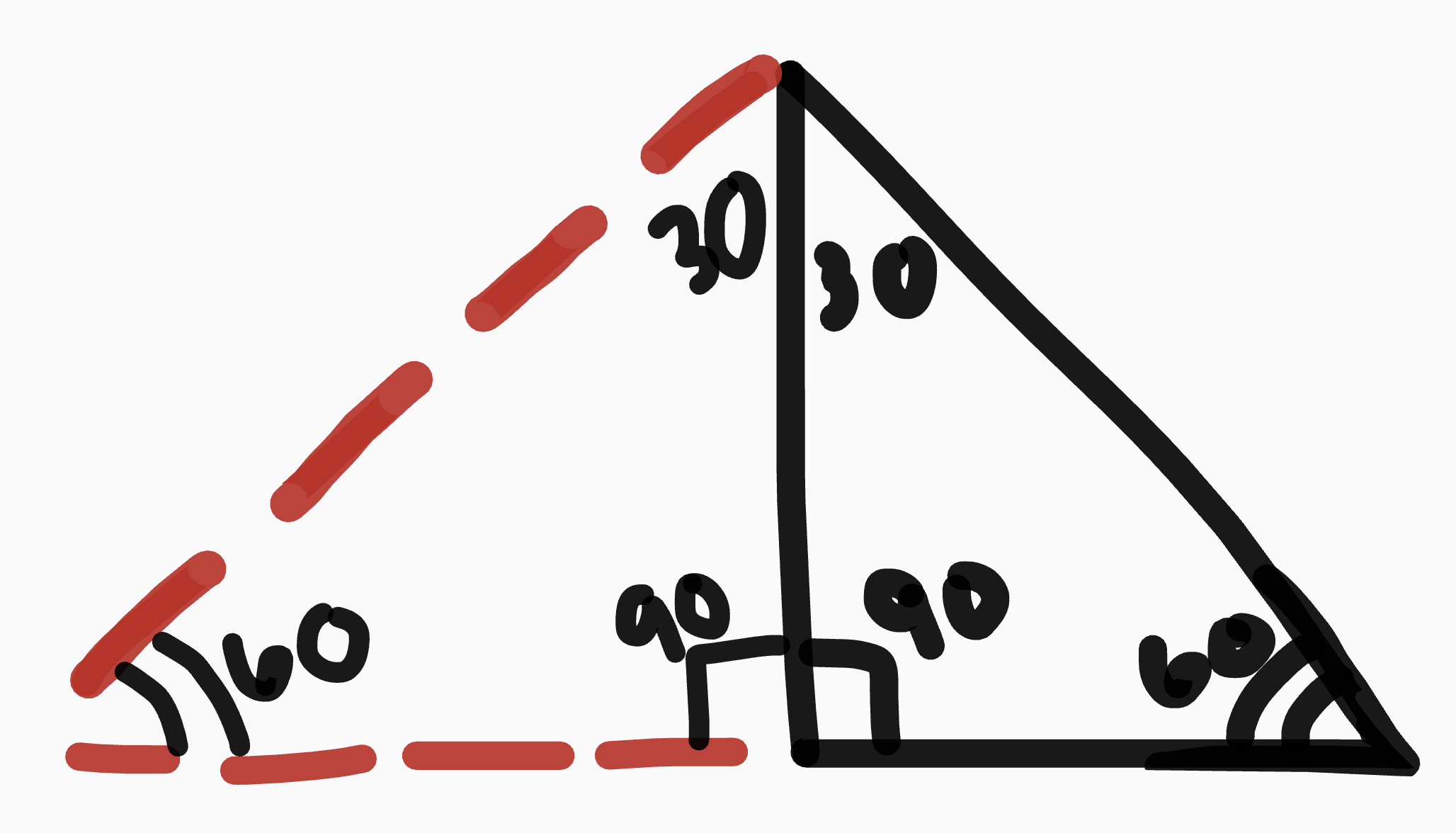
30-60-90

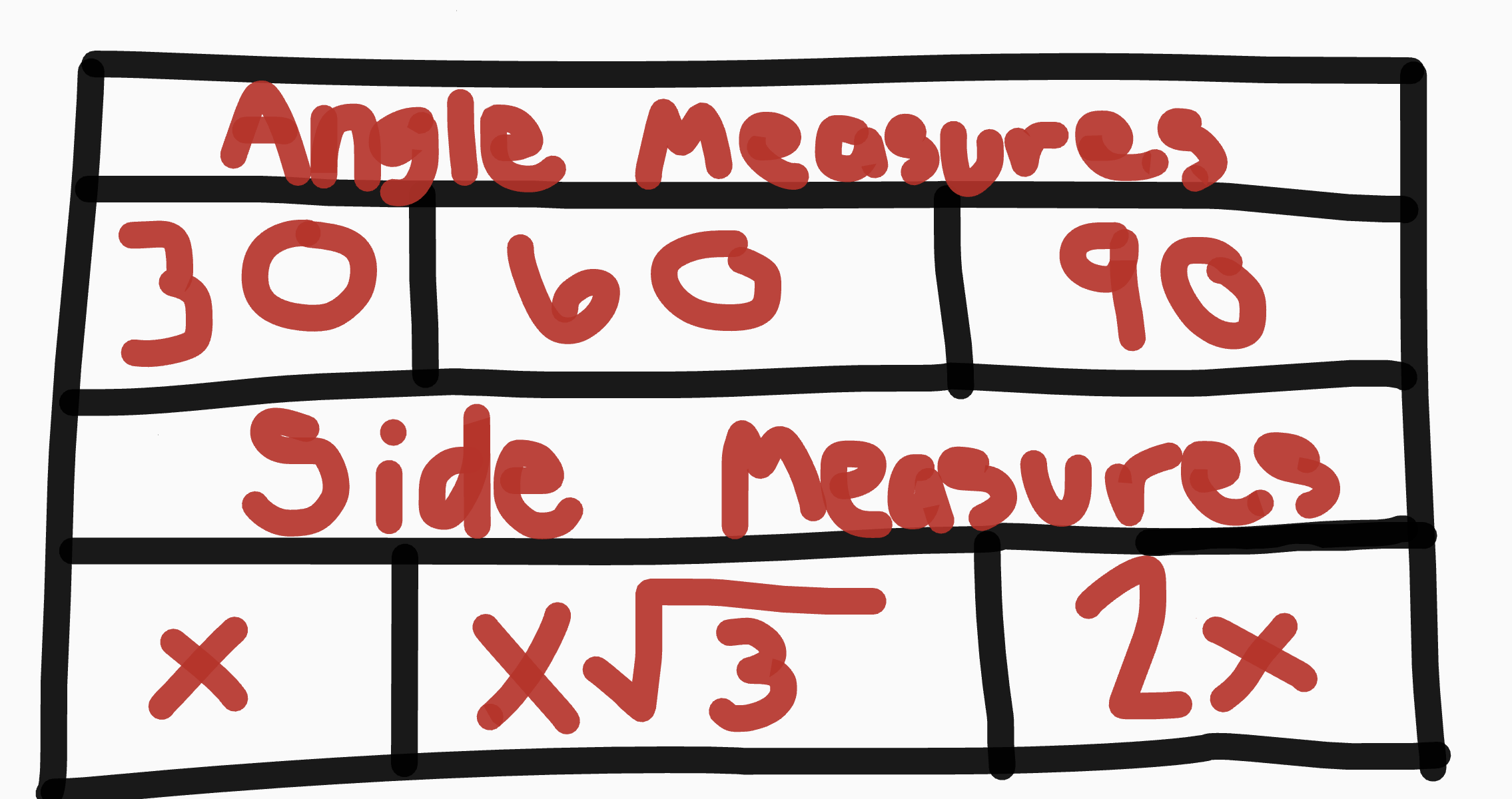
½ of an equilateral triangle

short side ½ hypotenuse

right scalene triangle

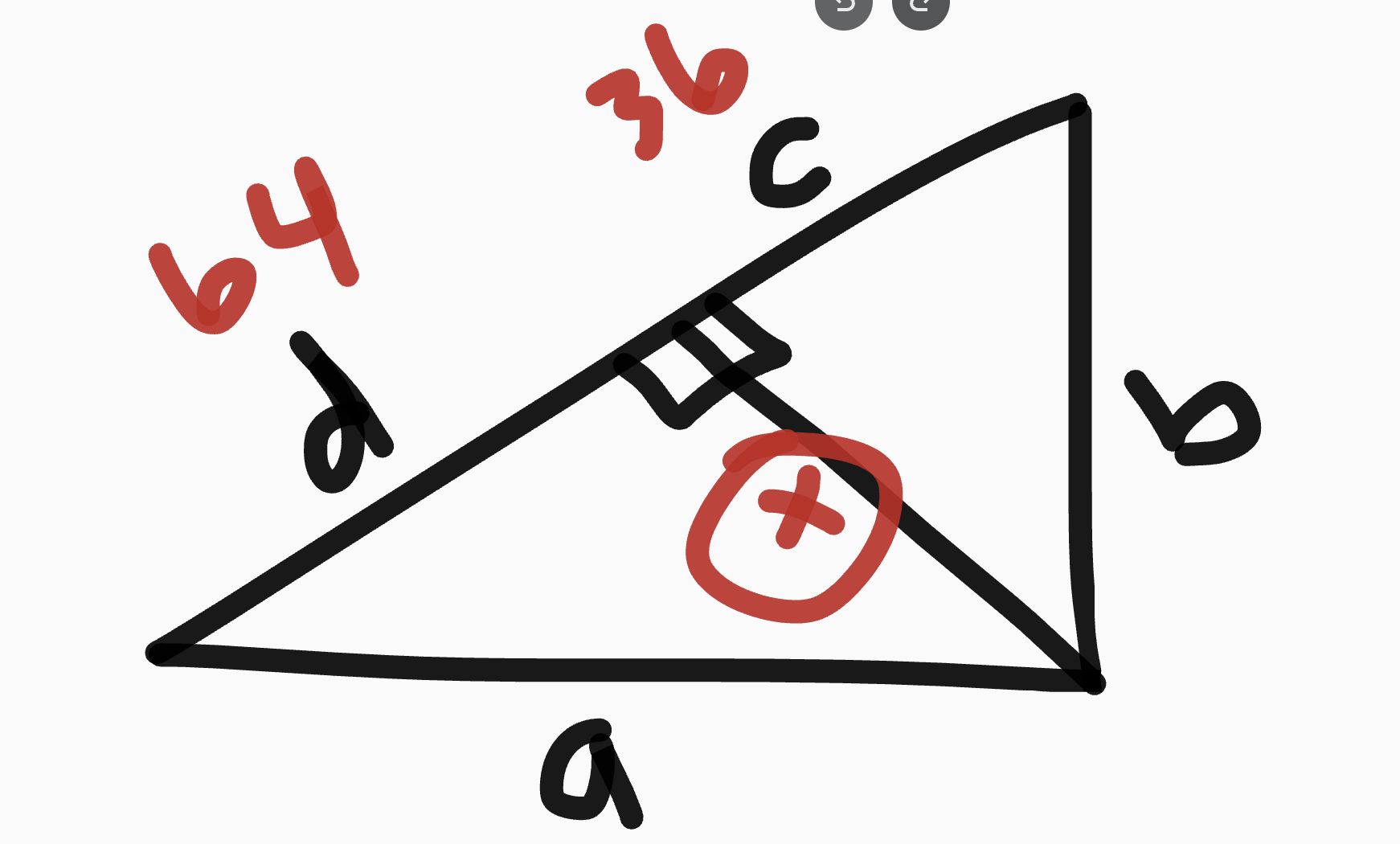
Right Triangles Similarity - solve for missing sides

c = 36

d = 64

x/64 = 36/x

cross multiply

x² = 2304

x = 48

TRIG RATIOS

TRIG RATIOS

SIN, COS, TAN

When to use SIN

when you know the H but want to know the O

When you know the O and H but want an angle

When to use COS

When you know H but want to know A

When you know A and H but want to know an angle

When to use TAN

When you know A but want to know O

When you know O and A but want an angle

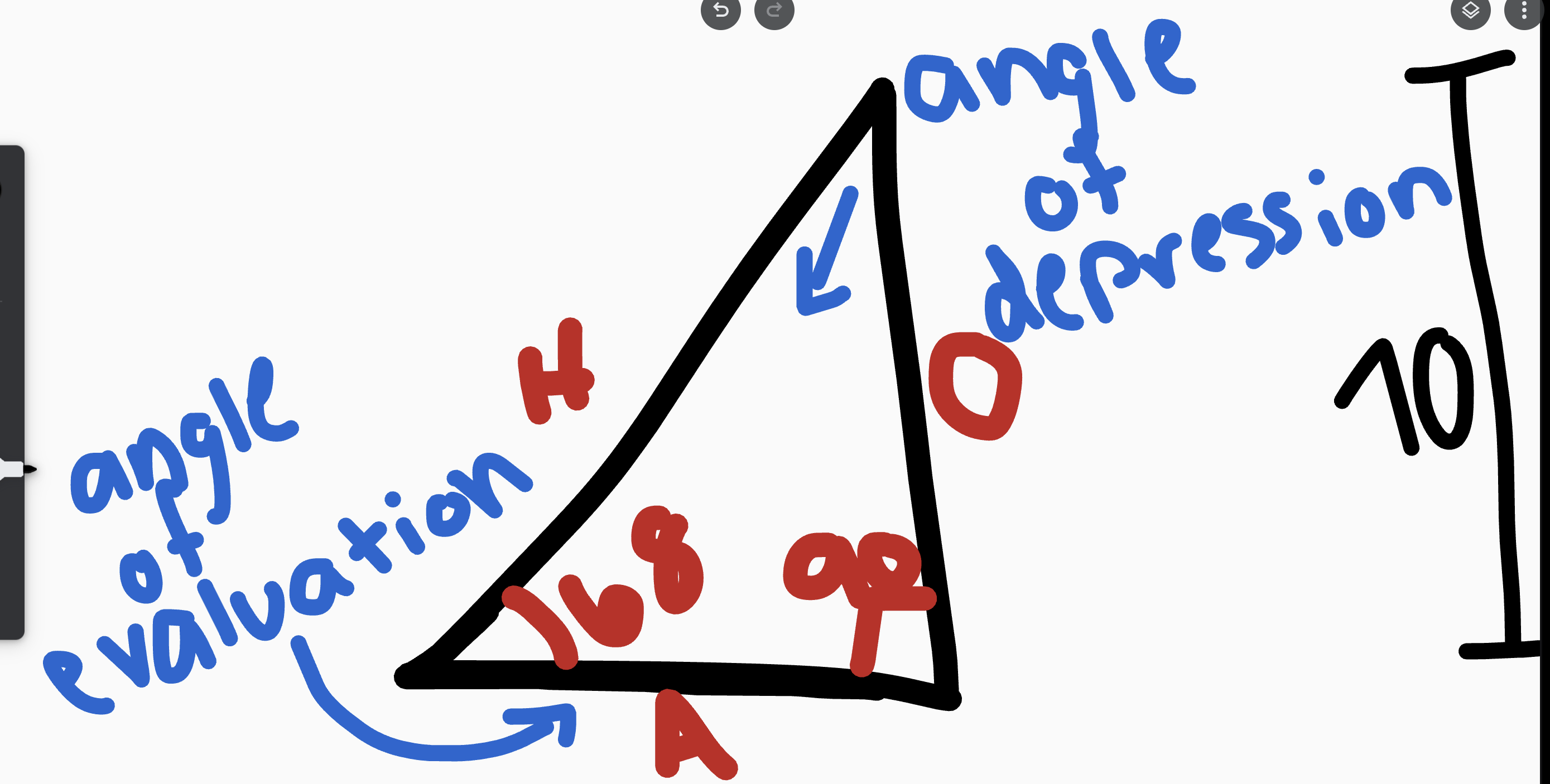
Triangle Vocab

(Hypotenuse, adjacent, opposite)

hypotenuse is across from the 90 degree angle

Adjacent is next to theta (the reference angle)

Opposite is across from reference angle

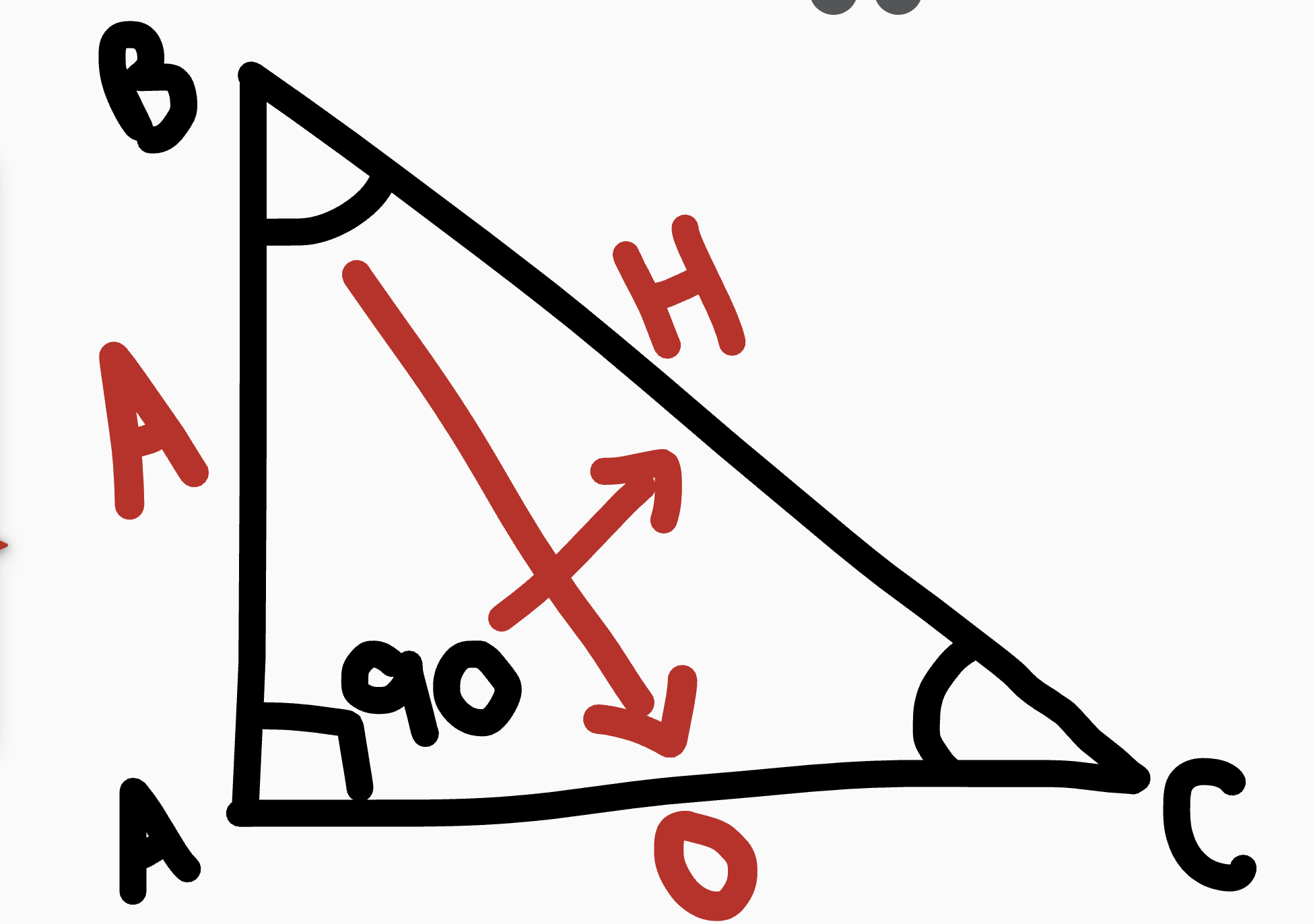
Steps to Finding Missing Sides

1) Identify the reference angle

2) Identify the given sides

3) Set up your equation

4) solve

example

reference angle = 68

given sides:

Opposite = 70

Hypotenuse = w

Sin 68/1 = 70/w

0.9272x = 70

divide 0.9272 on both sides

w = 75.5