F9 Regression

Deskriptiv statistik 5HP

Vad är regression?

En metod att sammanfatta riktade samband

Regression är en metod för att anpassa en matematisk modell som sammanfattar sambandet mellan variabler. Till skillnad från korrelation som bara mäter styrkan, kan regression bestämma hur en linje som beskriver sambandet ser ut.⁠⁠

Vad är en förklarande variabel (x-variabel)?

En variabel som (delvis) kan förklara värdet på en annan variabel

Vad är en responsvariabel (y-variabel)?

En variabel som kan förklaras av (beror av) en annan variabel

När används regression?

Regression används vid analys av riktade samband, när en variabel kan påverka en annan.⁠

Hur bestäms riktningen i ett samband?

Man avgör vilken variabel som påverkar och vilken som blir påverkad. Exempel: längd påverkar vikt för 19-åriga pojkar, körsträcka påverkar pris för begagnade bilar.⁠⁠​

Vilken variabel och vilken blir påverkad när vi studerar längd och vikt för 19-åriga pojkar?

Längden påverkar vikten

Vilken variabel påverkar och vilken blir påverkad när vi studerar pris och körsträcka för begagnade bilar?

Körsträckan påverkar priset

Vilken variabel påverkar och vilken blir påverkad när vi studerar försäljning och antal expediter i ett varuhus?

Det är inte tydligt vilket som påverkar vad

Vad är enkel linjär regression?

Enkel linjär regression innebär att man först bestämmer riktningen i sambandet och sedan anpassar en rät linje som bäst beskriver punktsvärmen i spridningsdiagrammet, genom att bestämma linjens placering och lutning.⁠⁠​

Terminologi i regression

x-variabel: Den förklarande (oberoende) variabeln som antas påverka y-variabeln⁠⁠​

y-variabel: Responsvariabeln (beroende variabeln) som antas bli påverkad av x-variabeln⁠⁠​

Enkel linjär regression: Används när vi har en förklarande variabel⁠⁠​

Multipel linjär regression: Används när vi har flera förklarande variabler⁠⁠

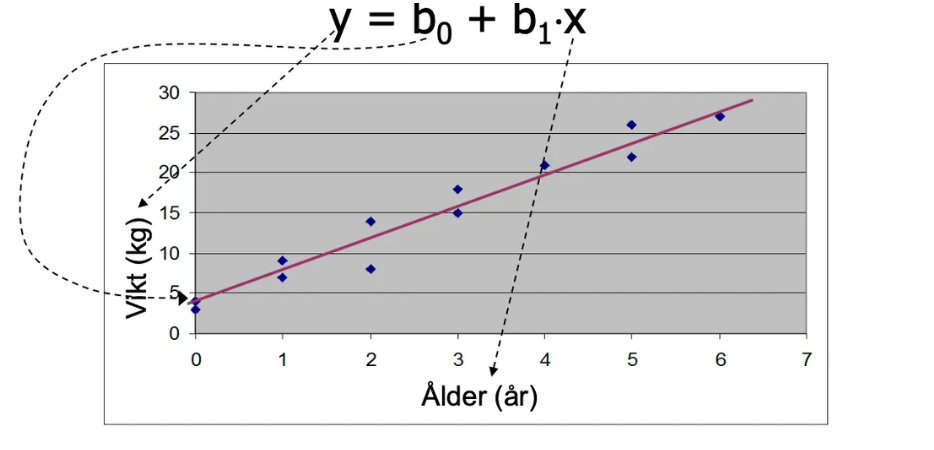
Matematisk beskrivning av en rät linje

Formel: y = b₀ + b₁x⁠⁠​

b₀ (intercept): Beskriver var linjen korsar y-axeln, värdet på y när x=0⁠⁠​

b₁ (riktningskoefficient): Beskriver linjens lutning - hur mycket y ändras när x ökar med 1 enhet⁠

Residual i regression

Definition: Det vertikala (lodräta) avståndet mellan en datapunkt och regressionslinjen⁠⁠​ (Avståndet mellan ett individuellt värde och den räta linjen i y-led)

Matematiskt uttryck: eᵢ = yᵢ - (b₀ + b₁xᵢ)⁠⁠​

Användning: Hjälper oss att mäta hur bra regressionslinjen passar till datapunkterna⁠⁠​

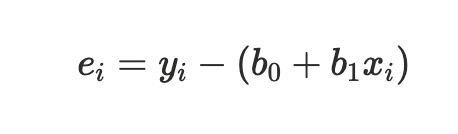
Vad är minsta-kvadrat-metoden inom linjär regression och hur används den?

Minsta-kvadrat-metoden används för att hitta den "bästa" regressionslinjen genom att minimera summan av alla kvadrerade residualer (avstånd) mellan observerade punkter och linjen.

Metoden ger följande formler för regressionskoefficienterna: (bild)
där b₀ är interceptet och b₁ är riktningskoefficienten i ekvationen ŷ = b₀ + b₁x⁠⁠​

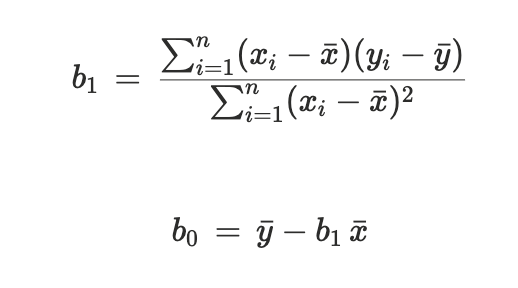
Exempel på Linjär Regression: Längd och Lungkapacitet

Regressionssamband mellan längd och lungkapacitet (FEV) med följande data:

Korrelation: 0,87⁠⁠​

Regressionsekvation: ŷ = -6,088 + 0,056·Längd⁠⁠​

Tolkning: För varje cm ökning i längd ökar lungkapaciteten med i genomsnitt 0,056 liter⁠⁠​

Alternativt: För varje dm längre, ökar lungkapaciteten med 0,56 liter⁠⁠​

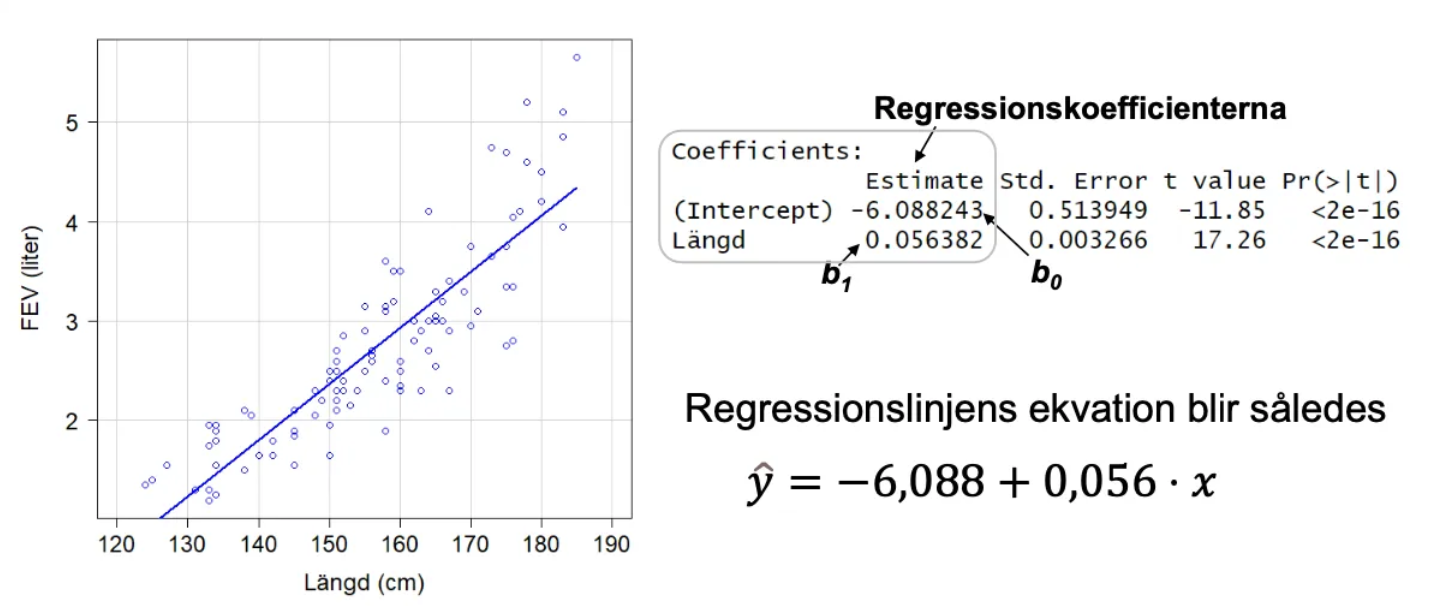
Är det här ett riktat samband? I vilken riktning i så fall, vilken variabel är den förklarande och vilken är responsvariabeln?

Längd är den förklarande variabeln och FEV är responsvariabeln

Varför lägger vi till en hatt ovanför y i regressionslinjens formel? För att visa att…

det är en skattning av genomsnittligt y med hjälp av regressionslinjen

Viktiga punkter om Regressionsanalys

Riktad samband: x = Längd (förklarande), y = FEV (respons)⁠⁠​

Interceptet (-6,088) är matematiskt korrekt men saknar praktisk tolkning eftersom längd=0 är utanför dataområdet⁠⁠​

Regressionslinjen passar bara inom spannet av befintliga data (ca 120+ cm)⁠⁠​

ŷ representerar en skattning av y-värdet, inte det faktiska värdet⁠⁠​

Vad är extrapolering?

Extrapolering är att dra slutsatser om värden utanför spannet av befintliga värden i ett stickprov. Sådana slutsatser är ofta felaktiga och bör undvikas.⁠⁠​

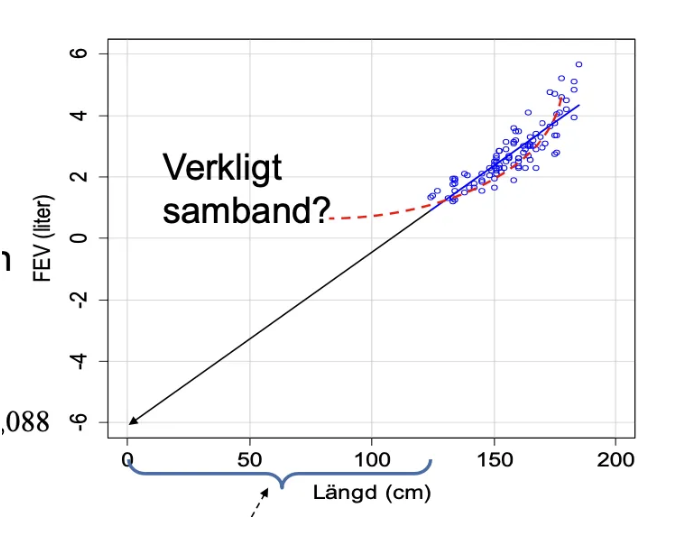
Extrapolering och interceptet

När x=0 ligger långt utanför befintliga värden i stickprovet, eller om x-variabeln inte kan anta värdet 0, kan interceptet (b₀) inte tolkas på ett meningsfullt sätt.⁠⁠​

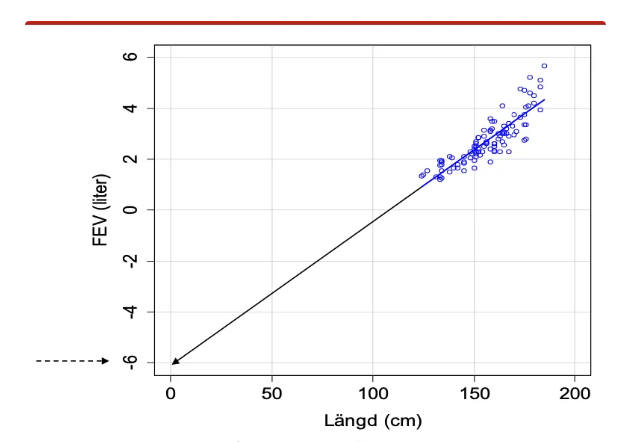
Regressionslinjen och extrapolering

Man bör inte anta att regressionslinjen kan sträckas ut utanför befintlig data. Interceptet visar endast var linjen skär y-axeln och påverkas inte av om den punkten har en relevant tolkning eller ej.⁠⁠​

Tolkning av regressionslinjen

Regressionslinjen ger genomsnittliga värden på y-variabeln för olika värden på x-variabeln⁠⁠.

Riktningskoefficienten b₁ (lutningen) visar hur mycket y-variabeln ändras i genomsnitt när x-variabeln ökar en enhet⁠⁠.

(Hur mycket Y förändras när X ökar en enhet)

Interceptet b₀ är medelvärdet för y-variabeln då x=0. Om 0 ligger långt ifrån stickprovets x-värden eller x inte kan anta värdet 0, kan interceptet inte tolkas⁠⁠.

((Genomsnittligt värde på Y när X är 0)

Begränsningar och syfte med regressionsanalys

Regression analyserar samband men kan inte fastställa kausalitet (orsak-verkan)⁠⁠.

En förändring i x-variabeln kan inte enbart utifrån regressionsanalys sägas orsaka en förändring i y-variabeln⁠⁠.

För att hävda kausala samband krävs andra vetenskapliga metoder⁠⁠.

Syftet med regressionsanalys

Undersöka hur sambandet mellan x och y ser ut i stickprovet (deskriptivt syfte)⁠⁠​

Uttala sig om hur sambandet ser ut i populationen med hjälp av statistisk inferens⁠⁠​

Prediktera värdet på y när vi känner till x (uppskattning när direkt observation saknas)

Stickprov vs population

Stickprovet används för att få information om populationen⁠⁠​

Regressionsanalys kan använda information i X-variabeln för att förbättra skattningen av medelvärdet för Y⁠

Regressionsmodellen

I populationen: y = β₀ + β₁x + ε (där ε är slumptermen)⁠⁠​

I stickprovet: ŷ = b₀ + b₁x (skattad modell)⁠⁠

Tolkning av riktningskoefficienten

Riktningskoefficienten (b₁) visar hur mycket populationsmedelvärdet för y påverkas av olika värden på x⁠⁠​

Prediktion med regressionsmodell

Exempel: ŷ = -6,088 + 0,056 · x där x är längd och y är lungkapacitet⁠⁠​

För x = 150 cm: ŷ = -6,088 + 0,056 · 150 = 2,312 liter⁠⁠​

För x = 140 cm: ŷ = -6,088 + 0,056 · 140 = 1,752 liter⁠⁠​

För x = 160 cm: ŷ = -6,088 + 0,056 · 160 = 2,872 liter⁠⁠​

Korrelationskoefficienten

Korrelationskoefficienten är ett mått på sambandets styrka⁠⁠. Den fungerar bra som relativt mått vid jämförelse av olika samband⁠⁠, men är svårare att tolka i absoluta termer⁠⁠.

Determinationskoefficienten

Determinationskoefficienten (R²) är besläktad med korrelationskoefficienten och anger hur stor del av variationen i responsvariabeln som kan förklaras av regressionsmodellen⁠⁠. Vid enkel linjär regression är R² = r² (kvadraten på korrelationskoefficienten).

Modell utan förklarande variabel

En regressionsmodell utan förklarande variabel (ŷ = b₀) ger en skattning där b₀ blir stickprovsmedelvärdet för y⁠⁠. En sådan modell saknar lutning och predikterar samma värde för alla observationer⁠⁠.

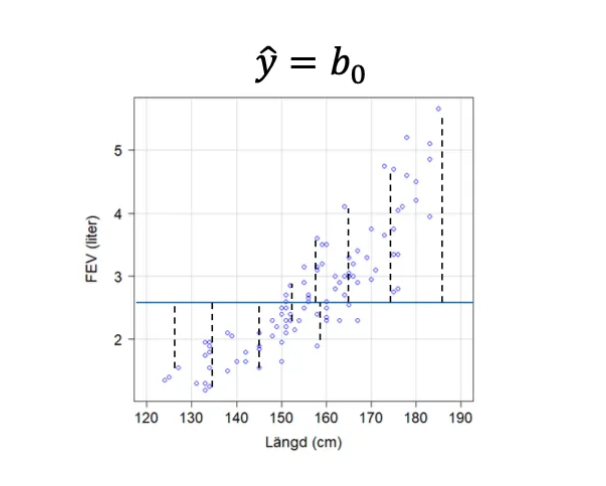
Förklarad variation

En modell med en relevant förklarande variabel har mindre spridning kring regressionslinjen och förklarar därmed en större del av variationen i responsvariabeln⁠⁠. Om 100% av variationen skulle förklaras av modellen skulle alla datapunkter ligga exakt på regressionslinjen⁠⁠.

Vad är determinationskoefficienten?

R² anger hur stor del av variationen i responsvariabeln (y) som regressionsmodellen lyckas förklara⁠⁠​

Värdet ligger mellan 0 och 1 (eller 0-100%)⁠⁠​

Vid enkel linjär regression sammanfaller R² med kvadraten på korrelationskoefficienten (r² = R²)⁠⁠​

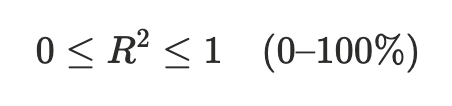
Tolkning av R²

Exempel: Om R² = 0,75 (75%) betyder det att 75% av variationen i responsvariabeln kan förklaras av den förklarande variabeln⁠⁠​

Det finns inga fasta tumregler för vad som är ett "bra" R²-värde⁠⁠​

I naturvetenskapliga sammanhang kan R² vara nära 1, medan i samhällsvetenskapliga sammanhang är det vanligt med värden under 0,5⁠⁠​

Även relativt låga värden (t.ex. 20%) kan vara värdefulla beroende på sammanhanget⁠⁠​

Regression med binär x-variabel

När en kategorisk variabel används i regression måste den kodas om till en binär dummyvariabel (0 eller 1). Tolkning av koefficienterna:

b₀ (intercept): Genomsnittligt y-värde för referenskategorin (x=0)⁠⁠​

b₁ (riktningskoefficient): Skillnaden i y mellan kategorierna (x=1 jämfört med x=0)⁠⁠​

Exempel: I pingvinmodellen ŷ = 4545,68 - 683,41 · Kön(hona) visar att honor väger i genomsnitt 683,41 g mindre än hanar, och hanar väger i genomsnitt 4545,68 g.⁠⁠​

Dummyvariabel

En dummyvariabel kan användas på samma sätt som en vanlig numerisk variabel i regressionsmodellen.

Hur tolkas riktningskoefficienten (b₁) när x är binär?

Riktningskoefficienten (b₁) är en skattning av hur mycket y-variabeln skiljer sig för den kategori som kodats till 1 jämfört med den kategori som kodats till 0.⁠⁠

Hur tolkas interceptet (b₀) när x är binär?

Interceptet (b₀) är en skattning av medelvärdet för y-variabeln för den kategori som kodats till x = 0.⁠⁠

Vad är Multipel linjär regression

Regression med fler förklarande variabler (x-variabler) i modellen.⁠⁠

ŷ = b₀ + b₁x₁ + b₂x₂⁠⁠

b₁ och b₂ tolkas som marginella förändringar

b₁ visar hur mycket y förändras när x₁ ökar en enhet (när x₂ hålls konstant)

b₂ visar hur mycket y förändras när x₂ ökar en enhet (när x₁ hålls konstant)⁠⁠

Interceptet (b₀): Värdet på y när alla x-variabler är noll⁠⁠​

R²: Mått på hur stor andel av variationen i y som kan förklaras av modellen.⁠⁠​

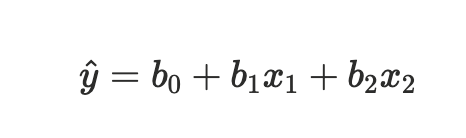
Hur tolkas b1 och b2 i en multipel linjär regressionsmodell?

Hur mycket Y förändras när X1 eller X2 ökar en enhet, givet att den andra X-variabeln hålls konstant

Att jämföra R² mellan olika modeller

R² blir alltid större när vi lägger till fler förklarande variabler, vilket inte automatiskt betyder att modellen blir bättre⁠⁠.

För att jämföra modeller med olika antal förklarande variabler bör vi använda adjusted R-squared som ökar med ökad R² men minskar med antalet förklarande variabler⁠⁠.

Adjusted R-squared visar hur stor andel av variationen i responsvariabeln som kan förklaras, justerat för antalet förklarande variabler i modellen⁠⁠.

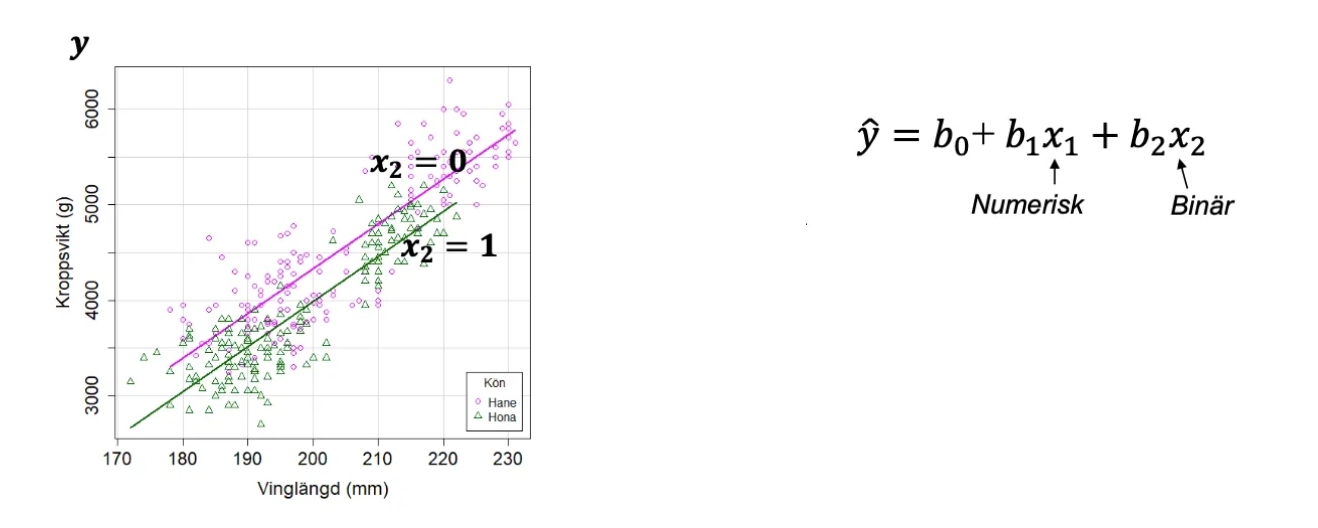
Visualisering av modell med binär variabel (Vad förväntar du dig att b1/b2 ska ha för tecken? Dvs förväntar du dig att sambandet mellan vinglängd och kroppsvikt ska vara positivt eller negativt?)

När en av x-variablerna är binär kan den skattade regressionsmodellen ritas som två parallella linjer i ett spridningsdiagram, en för varje kategori⁠⁠.

b₁ är lutningen på linjen (samma för båda linjerna)⁠⁠.

b₂ är avståndet i höjdled (y-led) mellan de två linjerna⁠⁠.

Positivt b1, Negativt b2

Multipel linjär regressionsmodell med två numeriska variabler

Formel: ŷ = b₀ + b₁x₁ + b₂x₂

Exempel: ŷᵏʳᵒᵖᵖˢᵛⁱᵏᵗ = -5737 + 48 · Vinglängd + 6 · Näbblängd⁠⁠​

Tolkning av koefficienter

b₁: Hur mycket y förändras när x₁ ökar en enhet och x₂ hålls konstant

b₂: Hur mycket y förändras när x₂ ökar en enhet och x₁ hålls konstant⁠⁠​

Exempel: Kroppsvikten ökar med 48g per mm vinglängd när näbblängd hålls konstant

Jämförelse av modeller

Använd adjusted R² för att jämföra modeller med olika antal förklarande variabler⁠⁠​

Exempel: Modell med vinglängd + näbblängd (R²ₐₗ = 0,759) vs. enbart vinglängd (R²ₐₗ = 0,758)

Slutsats: Ibland ger fler variabler inte mycket bättre förklaringsgrad

⁠⁠​

Är den multipla modellen med vinglängd och näbblängd som förklarande variabler bättre på att förklara kroppsvikten än den enkla modellen med vinglängd som ensam förklarande variabel?

Det är i princip ingen skillnad i förklaringsgrad mellan de två modellerna