Calculus 2 Section 8: Integration Techniques and Improper Integrals

Sorry, this will only help if you already have a solid understanding of the concepts!

The integral of a product…. (8.2)

is NOT equal to the product of its integrals

Formula for Basic Integration by parts (8.2)

∫udv = uv - ∫vdu

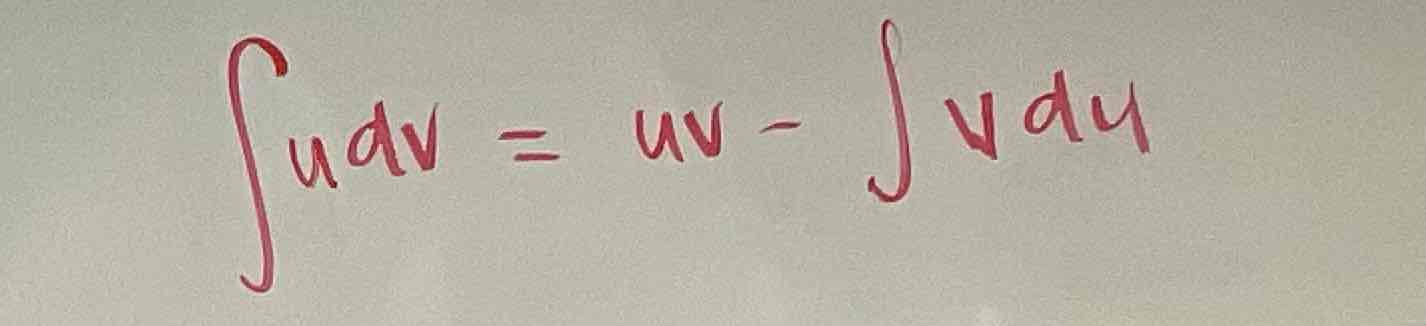
What is the rule for selecting u and dv during integration by parts (8.2)

Let u = the simpler derivative

Let dv = something you can integrate

(8.2)

∫csc(x) dx

∫csc(x)cot(x) dx

d/dx csc(x)

1. ∫csc(x) dx = -ln|csc(x)+cot(x)| + C

2. ∫csc(x)cot(x) dx = -csc(x) + C

3. d/dx csc(x) dx = -(csc(x)cot(x)) x¹

When do you use Tabular Integration? (8.2)

Useful when there is a power of x multiplied by a function with known integrals.

E.g. ∫x²cos(x) dx

What are the steps for tabular integration? (8.2)

use [∫x²cos(x) dx] as an example

hint (7 steps)

1. Set up three columns: label them signs, Us, DVs.

2. Under signs make repeating + and - signs.

3. Let X = U , let function = dv

4. Repeatedly differentiate Us (X) until 0

5. Repeatedly integrate DVs (the function) until lined with 0

6. Eliminate: First function, Last sign, the 0

7. Read across

When to use circular integration by parts? (8.2)

Used specifically for the form: (* = x)

[ ∫e²*sin(bx) dx ] or [ ∫e²*cos(bx) dx ]

Steps for Circular Integration by Parts (8.2)

use [ e²*sin(x) dx ] as an example

1. Keep the left hand integral (meaning left of the equal sign).

2. Integrate by parts twice

3. simplify (should end up with function similar to the left hand side).

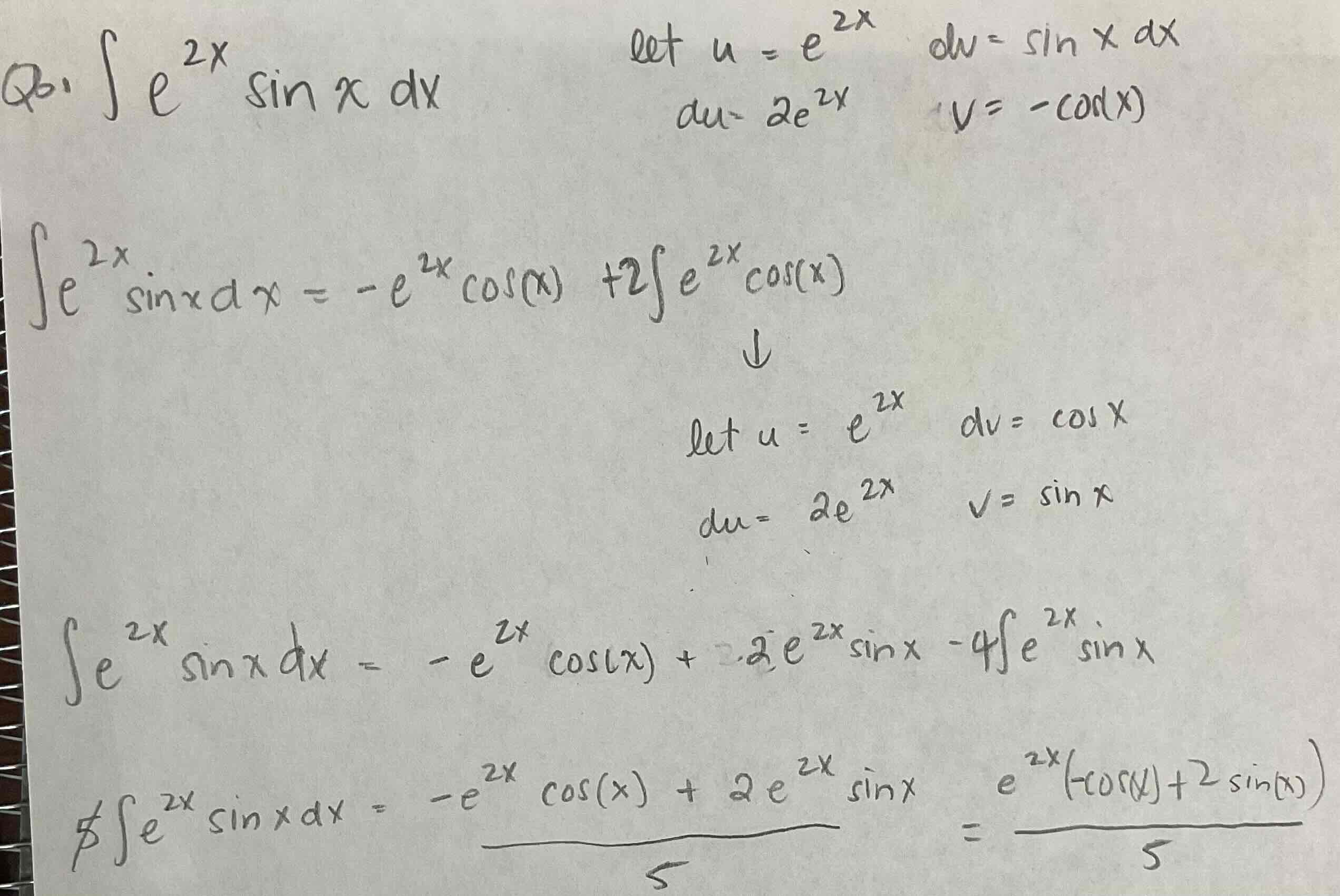
Rule for ln (or logs) when integrating by parts? (8.2)

Always let ln = u (we don’t have a method for integrating ln at this level in calculus)

(8.2) The three arc integrals/derivatives

arctan

arcsin

arcsec

18, 19, and 20 from image

What three substitution relationships are used the form [ ∫sin*(x)cos*(x) dx ] let * = numbers (8.3)

1. Pythag

2. Power reducing for sin²x

3. Power reducing for cos²x

What is the guideline when sine is odd and positive? (8.3)

1. Save one sine factor for du

2. covert the rest to cosine

3. Expand and then integrate (usually u-sub)

What is the guideline when cosine is odd and positive? (8.3)

1. Save one cosine factor for du.

2. Convert the rest to sines.

3. Expand and then integrate.

What is the guideline when the powers of both are even and nonnegative? (8.3)

Make repeated use of p-reducing formulas to make odd. Then follow Cosine (odd and positive) guideline.

What three relationships are used for integrating powers of secant and tangent [∫sec*xtan*x dx]

tangent identity

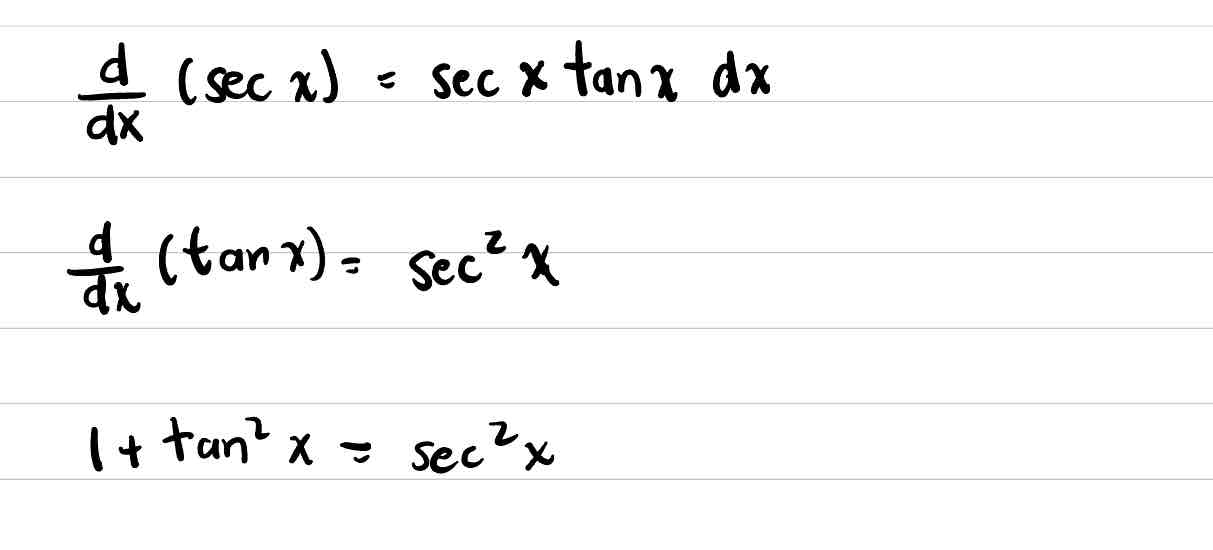
What is the guideline for when sec is odd and positive?

1. Save one secant squared for du

2. concert rest to tangents

3. expand and integrate

What is the guideline for when tangent is odd and positive? (8.3)

1. Save one secant-tangent factor for du

2. covert the rest to secants

3. expand and then integrate

Guideline when there are no secants, and the power of tangent is even and positive?

1. Convert a tangent squared factor to a secant squared factor.

2. Expand and then repeat if necessary

When there are only secants and the power is odd and positive? (8.3)

Use integration by parts

Guideline for when all guidelines fail?

Convert all to sines and cosines

What is trigonometric substitution used for? (8.4)

To eliminate radicals in the integrand

Explain the “Constant - Function” identity

1. For integrals containing √a²-u²

2. letting u = asinδ

3. then √a²-u² = acosδ

Explain the “Constant + Function” identity

1. For integrals containing √a²+u²

2. letting u = atanδ

3. then √a²+u² = asecδ

Explain the “Function - Constant” identity

1. For integrals containing √u²-a²

2. letting u = asecδ

3. then √u²-a² = atanδ

How do you complete there square to factor a quadratic equation? Using x²-6x+5 as an example

1. Half the coefficient of x

2. Square it

3. add then minus it

4. Factor with added number, simplify the other two

(x-3)² -9+5

When do we use partial fraction decomposition? (8.5)

When the denominator of an integrand is factorable or can be completed (and would other wise be solved by trigonometric substitution), decomposition may be preferable.

Name the 4 cases of partial decomposition and describe each (8.5)

Case 1: Distinct Linear Factors

Numerators will all be constants, None of the exponents repeat

Case 2: Repeated Linear factors

Numerator will still all be constant, denominators repeat to sum to power…

Case 3: Irreducible Quadratic Factor

Numerator will be Bx + c, denom will be irreducible quadratic

PLUS

One linear

Case 4: Repeated Quadratic

Numerator will be Bx + C, denominators repeat to sum to power

State the formula for trapezoidal numerical integration (8.6)

State the formula for Parabolic Numeric Integration (Simpson’s Rule) (8.6)

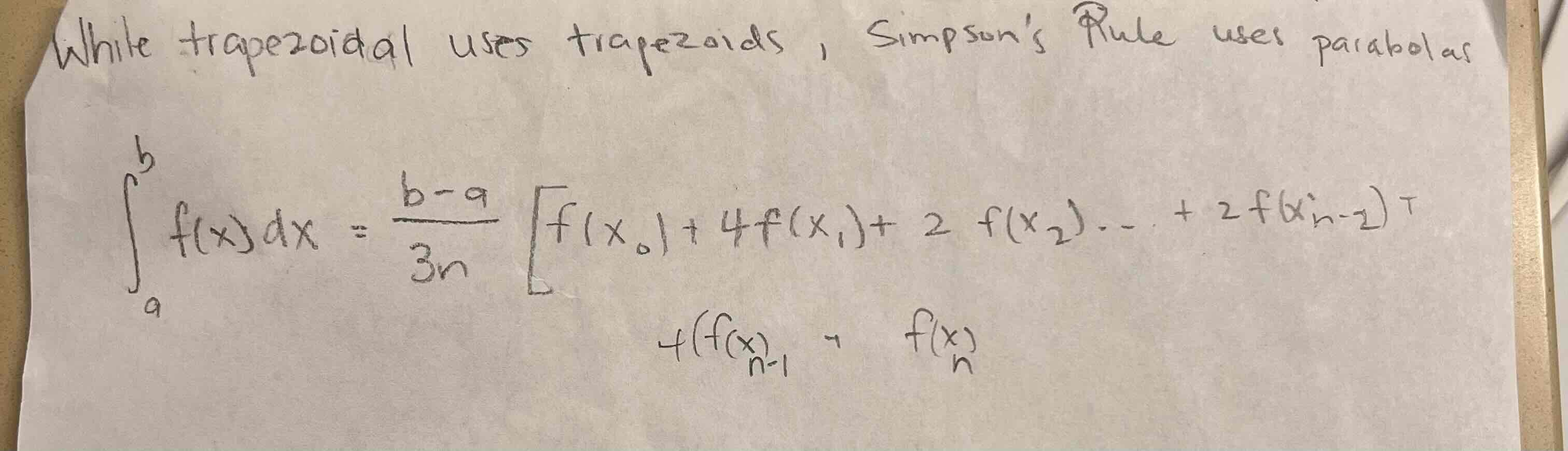
What must we do when the numerator is SAME or larger power than the denominator in partial decomposition?

Long division. ALWAYS

In what two (general) occasions does an improper integral occur?

1. When one of the limits of integration is ∞ or -∞

2. When the integrand has an internal discontinuity