Basics of Complex Numbers & Imaginary Numbers ! ⭐

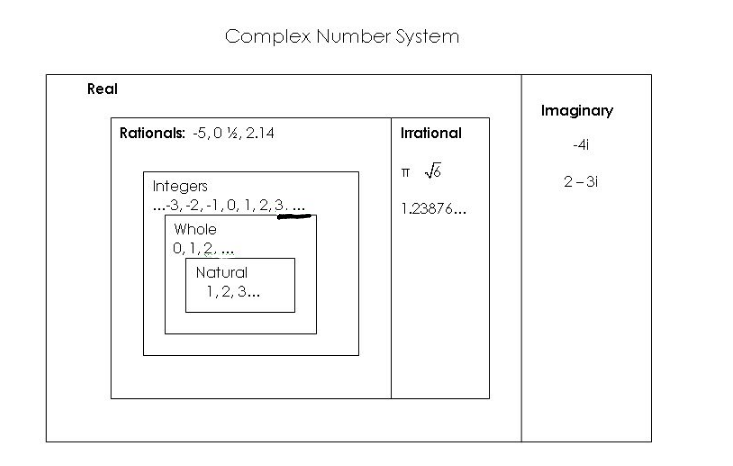
what is the complex number system?

• imaginary numbers and real numbers make the complex number system

what is an imaginary number?

• i = a number whose square is -1

• written form: a + bi

  • b does not equal 0

  • 4 + 3i , -5 + 9i

• when squaring = √-9 = ± 3i , √144 ± 12i

  • all these work because √-1 = i , i² is -1 , every negative number can be -a, can be broken by -1a

what is the pattern of imaginary numbers?

• it repeats itself every 4th number

• these are your REMINDERS

  ex: reminder of 7 is equal to -i

what determines the answer in imaginary number?

• the reminders

• i taken to a power that is a multiple of 4 is always 1

  • when dividing the exponent by 4 the remainder will determine what your answer is

  • i^4(#) will always be 1 if it is a multiple of 4

reminder of 1

i

how would we solve i99

• the closest mutliple of 4 that’s close to 99 is 96

  • i96

• now there is a reminder of 3

  • i3

• the answer is now: -i

how would we solve i7321?

• change the answer to something that can be divisible by 4

  • 7320

  • we know can be divided by 4

    • because any thousand is divisible by 4 any hundred is divisible by 4 and 20 is divisible by 4

• i ^7320 • i^1

  • since there is a reminder of 1 the answer is i

  • according to the chart