Week 3 – Mathematics as a Language

Bachelor of Science in Medical Technology (1st Year): MATHEMATICS IN MODERN WORLD

• a system of conventional spoken, manual (signed), or written symbols by means of which human beings, as members of a social group and participants in its culture, express themselves.

Language

Language itself is: (3)

1. Precise

2. Concise

3. Powerful

• It can make very fine distinctions among set of symbols.

Precise

• It can briefly express long sentences

Concise

• It gives upon expressing complex thoughts

Powerful

“and” is equivalent to

Plus (+)

“is” may have

different meaning

ones used for counting

“Cardinal numbers”

ones used for telling positions

“Ordinal numbers”

used only as a name to identify something

“Nominal numbers”

Addition Key Words (+)

1. Increased by

2. More than

3. Combined, together

4. Total of

5. Sum, plus

6. Added to

7. Comparatives (Greater than, etc)

Subtraction Key Words (-)

1. Decreased by

2. Minus, less

3. difference between/of

4. less than, fewer than

5. left, left over, after

6. save (Old fashioned term)

7. Comparatives (Smaller than, etc)

Multiplication Key Words (.) (x) ()

1. Of

2. Times, multiplied by

3. Product of

4. Increased/decreased by a factor of (this last type can involve addition or subtraction and multiplication)

5. Twice, triple, etc.

6. Each (They got three each, etc.)

Division Key Words (a/b) (a:b) (÷)

1. Per, a

2. Out of

3. Ratio of, quotient of

4. Percent (Divide by 100)

5. Equal pieces, split average

Equals Key Words (=)

1. Is, are, was, were, will be

2. gives, yields

3. sold for, cost

For the set of natural numbers

• N

• Ex: N= {x/x = 1,2,3, 4...}

For the set of integers

• Z or I

• Ex: Z or I = {x/x = 1, -1,1,2, -2,3, -3,}

For the set of all positive integers

• Z⁺ or I⁺

For the set of all rational numbers

• Q

• Ex: Q = {x/x ∈ I or x = a/b, where b≠0}

For the set of all positive rational numbers

Q⁺

For the set of irrational numbers

• P

• Ex: P = {x/x ∉ Q}

For the set of all real numbers

• R

• R = {x/x ∈ Q or P}

• Students can connect one number with one object then count them with understanding.

One-to-one Correspondence

• Tells how many things are in a set.

• When counting a set of objects, the last word in the counting sequence names the quantity for that set.

Cardinality

• A set S having all its elements as sets is called _____

• For example:

  S = { {1, 2}, {2, 4}, {3, 5, 7} }

Set of sets

• Two finite sets A and B are equivalent if their cardinal number is same, i.e., n(A) = n(B).

Equivalent sets

• Two sets A and B are said to be equal if every element of A is a member of B, and every element of B is a member of A.

Equal sets

Any set of ordered pairs

Relation

• A type of relation where there is exactly one output for every input.

• For every x there is exactly one y.

Function

• serves as a set of rules that govern the structure and presentation of mathematical proofs.

• It allows us to determine the validity of arguments in and out of mathematics.

• A proposition is a statement that is, by itself,

  either true or false. They can be expressed in

  symbols P, Q, R, or p, q, r.

Logic

means single idea statement

Simple

conveys two or more ideas

Compound

is a statement that is either true or false, but not both.

Proposition

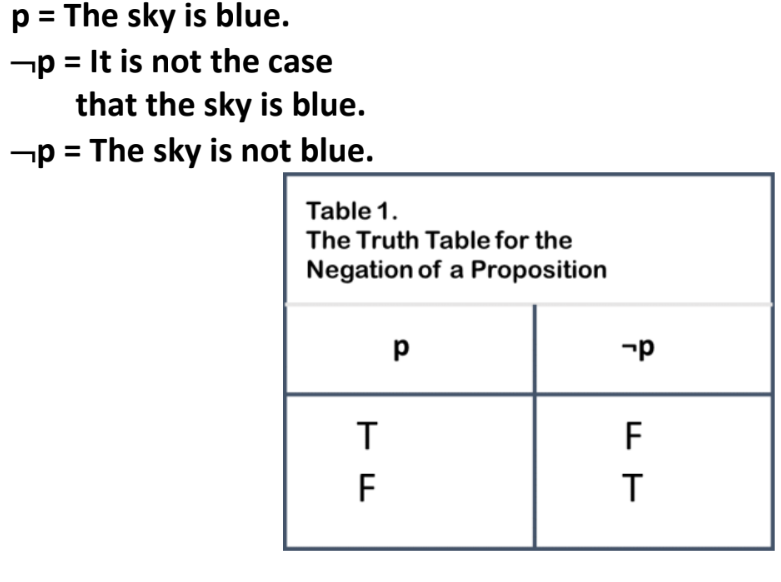
• Let p be a proposition. The statement “It is not the case that p” is also a proposition, called the _______, or ¬p (read “not p”)

Negation of p

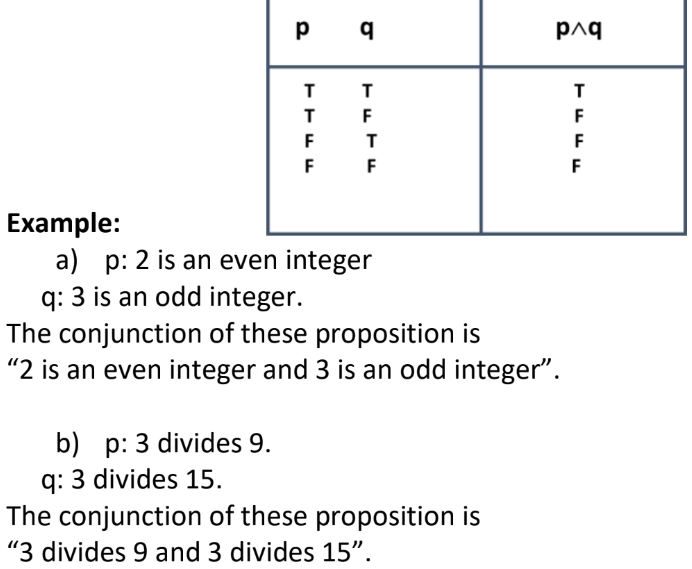
• Let p and q be propositions. The proposition “p and q,” denoted by pq is true when both p and q are true and is false otherwise.

Conjunction of p and q

• Let p and q be propositions. The proposition “p or q,” denoted by pq, is the proposition that is false when p and q are both false and true otherwise.

Disjunction of p and q

• Let p and q be propositions. The implication p→q is the proposition that is false when p is true and q is false, and true otherwise. In this implication p is called the hypothesis (or antecedent or premise) and q is called the conclusion (or consequence).

Implication p→q