Macro - Topic D : The long run

SR vs MR vs LR

SR - business cycles

MR - Revert to norm

• These are dominated by shocks & policy

LR - K accumulates + tech change dominates

Very LR - tech change dominates even more

Neoclassical growth model (with tech progress) assumptions

Assume L augmenting tech progress - As tech improves it makes L more productive

Constant RtS

Diminishing returns to inputs (K / AN)

State of technology

A

Output per unit of effective L

Y / AN = F (1/AN * K , 1) → y_AN = f(K_AN)

Savings and MPC

S = 1 - MPC

I, S and Output → k_AN

I = S = sY

I / AN = sY/AN

I / AN = sy_AN

i_AN = sf(K_AN)

Inflow of K per effective L (+∆k_AN)

i_AN = sf(K_AN)

Output per effective L graph

K, AN increase over time

A, N growth exogenous - but constant

K growth endogenous

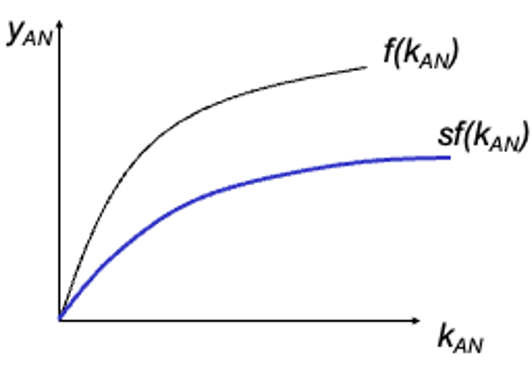
Effective L

AN

Growth rate of effective Labour

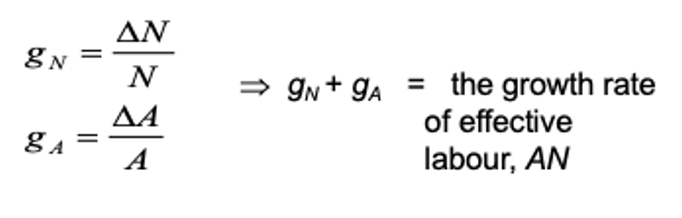
Investment needed to maintain a constant level of K per unit of effective worker

(δ + g_N + g_A) k_AN

Every time period some tech wears out (at a constant rate)

Outflow of capital per effective worker (-∆k_AN)

d_AN = (δ + g_N + g_A) k_AN

Dynamics of capital

Blue line = inflows & Green line = outflows

In equilibrium K/AN ratio constant → If not at equilibrium it will converge

Model shows us countries have different per capita incomes due to varying savings rates

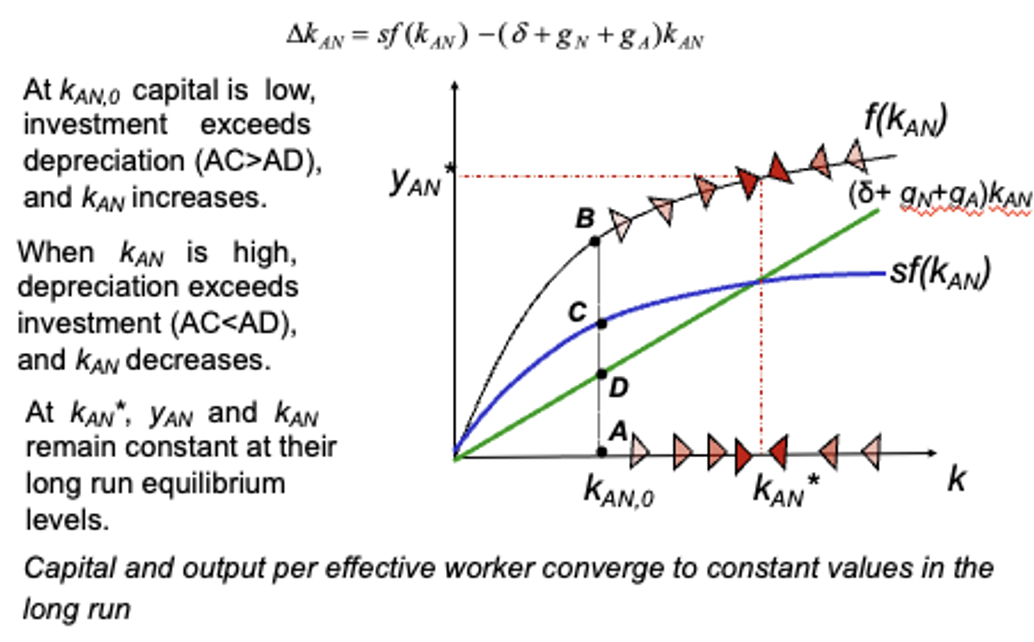
K & Y per worker in steady state

They both grow at the rate of tech progress (g_a)

y_AN = Y/AN = y/A → g_^yAN = g_y - g_a

In steady state g_^y*_AN = 0 → g_y = g_a

What affects the steady state?

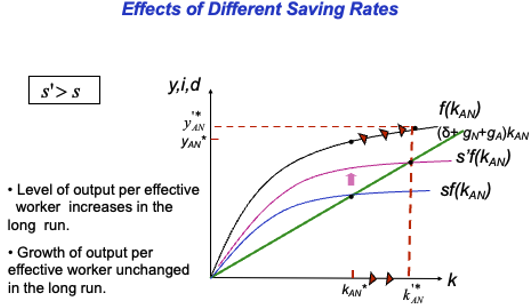
Savings rate increase

Growth rate of tech progress (g_a) changes

Savings rate increase

s’ > s → K inflows increase → K/AN (k_AN) increase → line shifts

Level of output per effective worker increases in LR → higher growth until economy reaches new steady state (same growth rate)

Growth of output per effective worker unchanged in LR

Crowding in

Increased government spending or investment leads to greater private sector investment → I increases

• due to spare capacity + confidence boost + complementary public I

In LR this increases Y

Growth rate of tech change / progress changes (g_A)

SS shocks cause this

g_a > g’_a → Outflows of K slow → K/AN rise → gradient shallower

Level of output per effective worker increases in LR → higher growth unti; economy reaches new steady state (same growth rate)

Growth of output per effective worker unchanged in LR

Growth of output per worker falls

Limitations of LR model

• Model doesn’t explain what are the determinants of the technological progress (g_a exogenous)

• Doesn’t explain lack of convergence in poorest economies

• Suggests that differences in per capita income are due to differences in K.

  • In practice H & A important

• Productivity is absent from model

Determinant of tech progress

R&D spending

What does spending on R&D depend on

• The fertility of the research process

• The appropriability of research results

The fertility of the research process

how spending on R&D translates into new ideas and new products

The appropriability of research results

the extent to which firms benefit from the results of their own R&D