yr2- gravitational fields
1/19
There's no tags or description
Looks like no tags are added yet.
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
20 Terms
Relationship between a test mass and a main body mass
The gravitational field of the main body mass is much larger than the test mass, this is immeasurable to the main body mass.
What do gravitational field lines represent?
what do they look like acting on a main body mass?
They represent the direction of the force acting on the test mass due to the main body mass, the closer they are, the stronger they are
They are radial and converge when we move closer to the earths core and diverging when we move away from the core.
Field lines properties?
they are uniform and parallel if we were to imagine them on a flat surface as we can say that the density of the volume of the mass is constant throughout
they are always perpendicular to the surface
Constant of proportionality?
6.67 × 10-11
Newtons law of gravitation?
The idea that the force of attraction is directly proportional to the product of the two masses and inversely proportional to the square of the distance between them
F = GMm/r2
Gravitational field strength?
Force acting upon every unit of of mass
g = f/m
Can also be defined by the potential gradient where g = -delta V /delta r
derive an equation for g using the definition of g
g= f/m while f=GMm/r2 therefore if we divide GMm/r2 by m , we get g = GM/r2
how does g vary while on earth?
g at the centre= 0, g on the surface=9.81
Gravitational potential?
The work done per unit mass to move an object from infinity to a point in a gravitational field. It is defined as V = work done/ mass
Can also be defined as V= - GM/r
Equipotential surface?
The point at which 0 work is done to overcome the force of attraction
They follow the shape of the object
They are perpendicular to the field lines
The work done to move an object each time is the same if we have 100J as mass is constant.
This consistency allows us to move the object with the same energy but increasing the distance it moves each time
Follows the potential gradient where the negative sign can symbolise the work being applied to overcome the force of attraction
Orbital speed?
Well if centripetal f=mv2/r and gravitational f=GMm/r2 then mv2/r=GMm/r2, so v2= GM/r , v = (GM/r)1/2
Orbital kinetic energy?
This only applies when objects are at a distance r away from the earth not at the SURFACE of the earth.
1/2m ((GM/r)1/2)2 = GMm/2r
Potential energy?
Ep/m = -GM/r so Ep= -GMm/r
Total energy?
Orbital kinetic energy+potential energy
GMm/2r +(-GMm/r)
GMm/2r-2GMm/2r= -GMm/2r
Launching a satellite from the surface of the earth?
we need a linear kinetic energy to launch it into the atmosphere. this must be equal to the gravitational potential energy, orbital potential and the orbital kinetic energy.
1/2mv2=-GMm/r+(-GMm/R)+GMm/2r
orbital ke is half of the gpe
escape velocity?
speed needed to escape the gravitational field
here there will be no orbital kinetic as we are at the surface of the earth
the gravitational potential is 0 as we are at the surface of the earth
therefore 1/2mv2=0-(-GMm/R)
escape velocity = v = (2GM/R)1/2
What does the negative truly represent in the -GM/r?
The negative represents that we have to do work to pull a mass away from the earths force of attraction however no work is required to pull the mass towards the earth due to a natural force of attraction due to the main body mass, the earth
Kepler’s Third law-equation
T²=(4 pi²/GM)r³
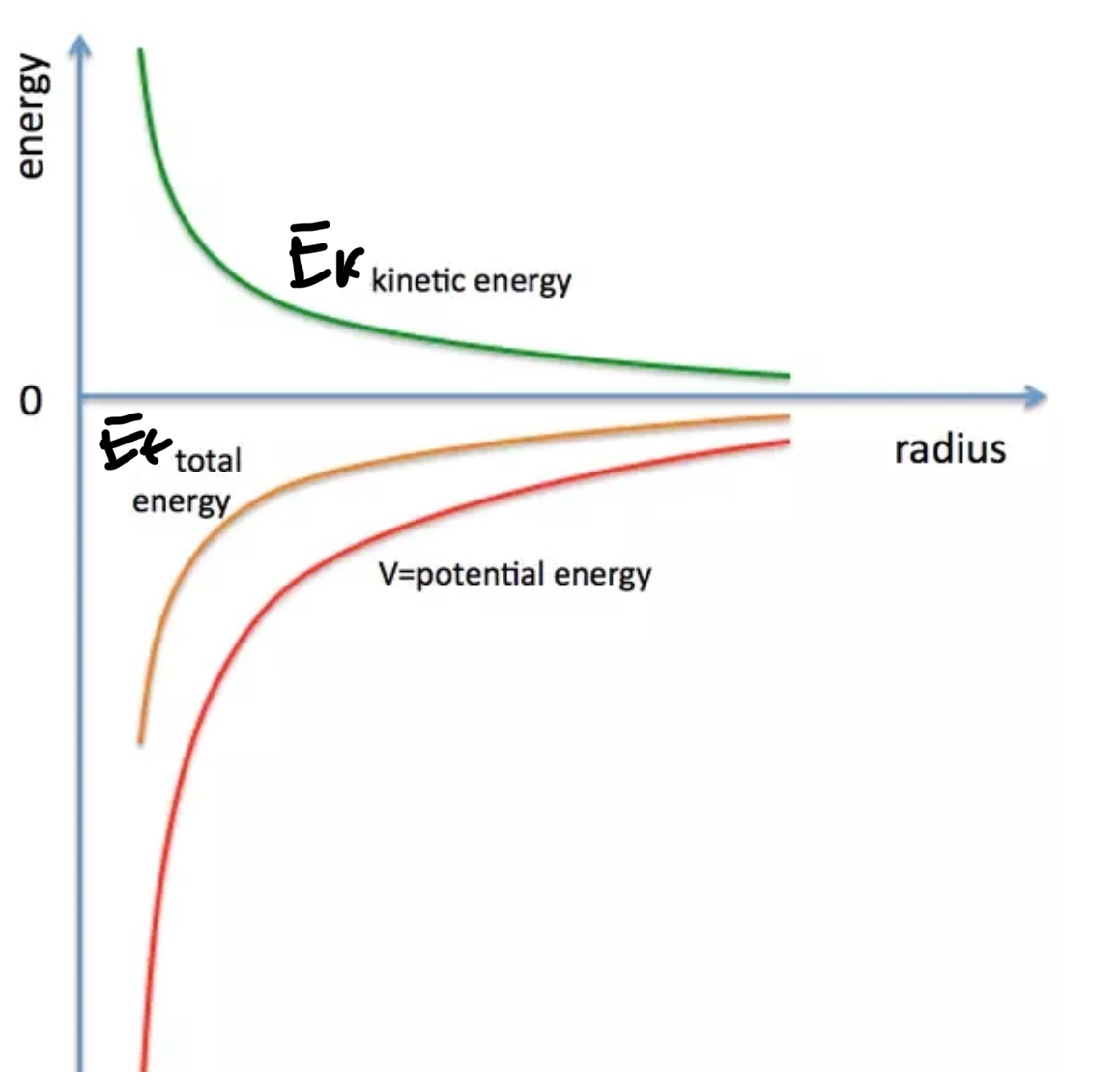
Gravitational energy graph
Orbital kinetic energy = GMm/2r : follows a positive inverse square law
Potential energy = -GMm/r : follows a negative inverse square law
Total energy = -GMm/2r : follows a negative inverse square law
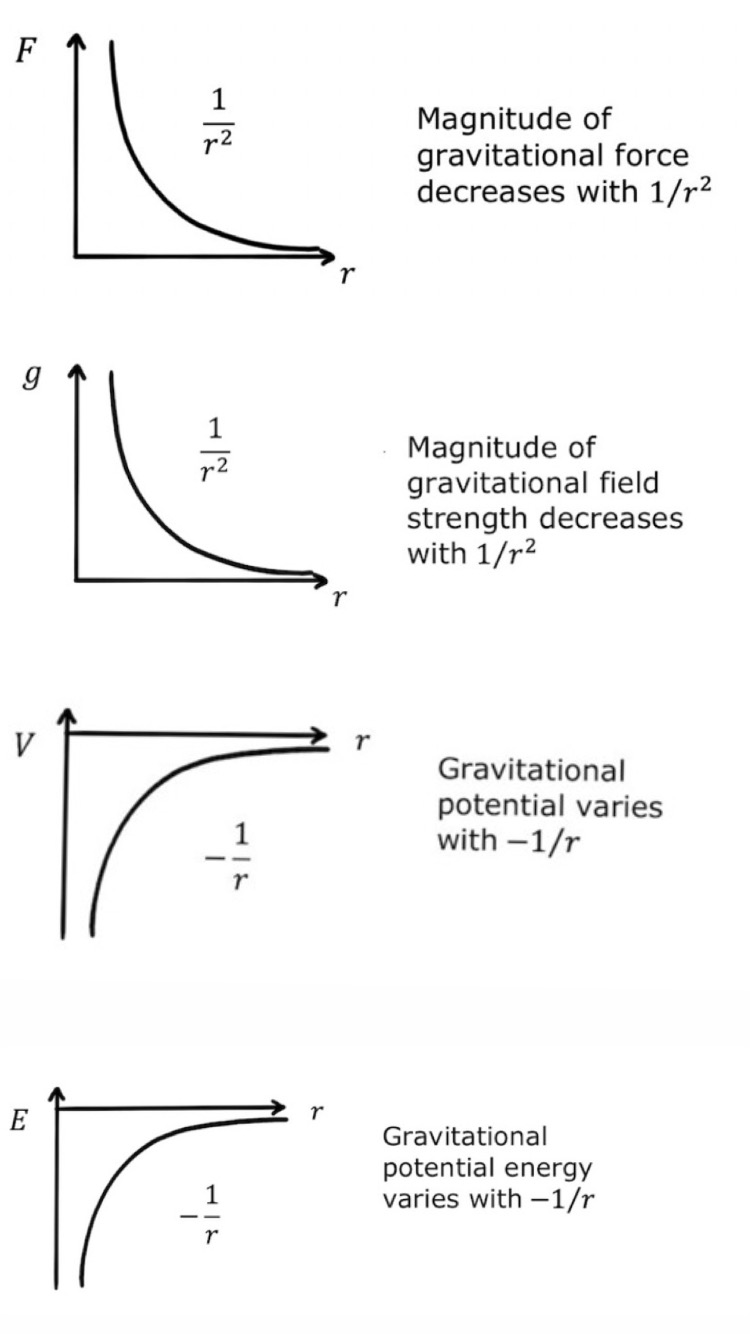
Inverse square law?
Applies to equations that have an r at the bottom
F=GMm/r² - newton’s law of gravitation
g=GM/r² - gravitational field strength
E=-GMm/r - gravitational potential energy
V= GM/r - gravitational potential