Unit 1: Limits and Continuity

Basic Limit Rules

Basic Limit Rules

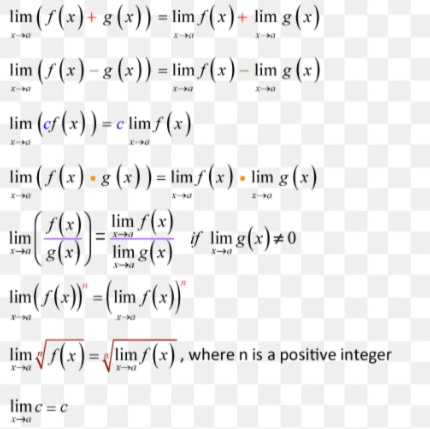
Limit Identities

• lim(sinx/x)=1

• limx→0(1-cosx/x)=0

• limx→0(x/sinx)=1

• limx→0(cosx-1/x)=0

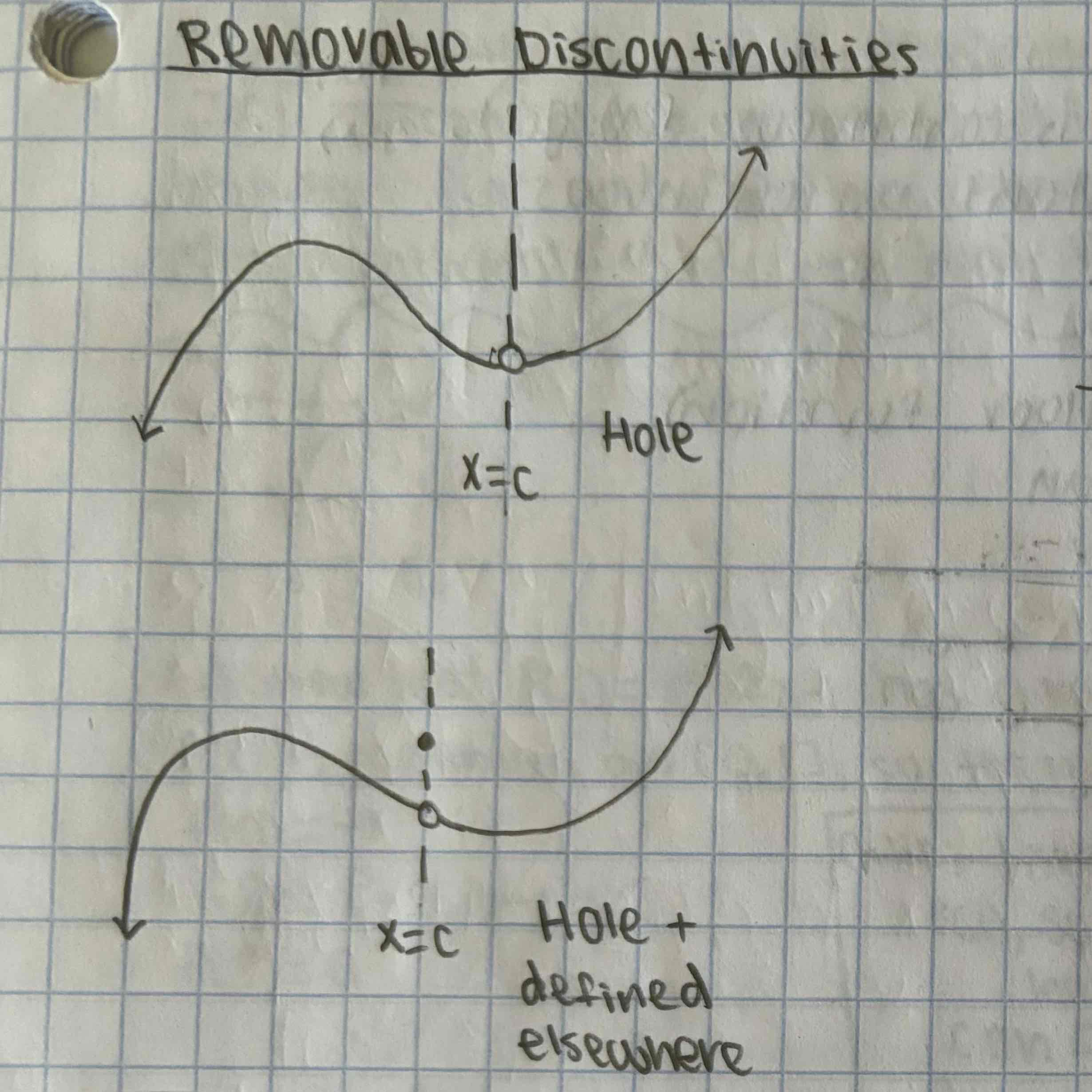
Removable Discontinuities

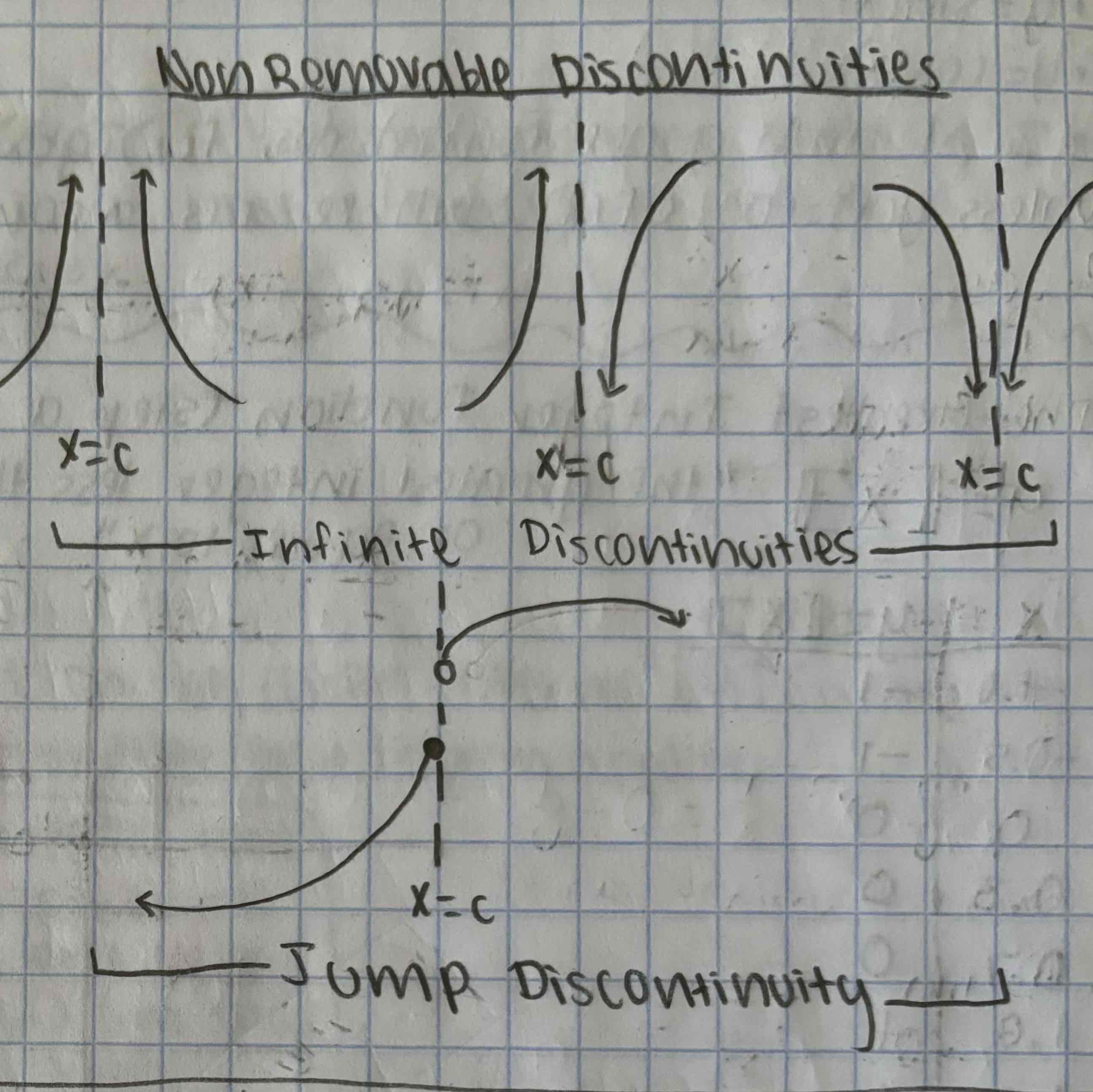
Non-Removable Discontinuities

Continuity at a Point

When can you assume a function is continuous?

• The function is a polynomial

• y = sin(x)

• y = cos(x)

• If f and g are continuous, f(x) ± g(x) is continuous, f(x) g(x) is continuous, f(x)/g(x) is continuous where g(x) does not equal 0, and c * f(x) is continuous where c is a constant

Vertical Asymptote

x=c is a vertical asymptote if the limx→c⁺ f(x) = ∞/-∞ and the limx→c⁻ f(x) = ∞/-∞

Horizontal Asymptote

y=b is a horizontal asymptote if the limx→∞/-∞ f(x) = b

Properties of Infinite Limits

Squeeze Theorem

If f(x) ≤ g(x) ≤ h(x) for all x ̸= a and limx→a f(x) = limx→a h(x) = L, then
limx→a g(x) = L

When does a limit not exist?

• f(x) approaches a different number from the right as it does from the left as x→c

• f(x) increases or decreases without bound as x→c

• f(x) oscillates between two fixed values as x→c

Horizontal Asymptote Rules

• If top degree = bottom degree, divide leading coefficients

• If top degree < bottom degree, ha is at y = 0

• If top degree > bottom degree, there is no ha

limx→0(asinbx/ctandx)

ab/cd

limx→0(sinax/x)=

a

limx→0(sinax/sinbx)=

a/b