Summative Test 2

Oxygen gas is at a P=10.16 MPa, T=178.02 K.  The critical pressure  and temperature for oxygen are Pc=5.08  MPa and Tc=154.8 K respectively.  Compute Pr and Tr and use the compressibility chart to determine the value of Z. The approximate value of the compressibility factor Z is 

0.48

Problem statement for Questions 2 to 4

A closed system that has rigid walls with a volume V=8 m³ contains air (assumed to be ideal gas) at a pressure P1=200  kPa and temperature T1=27 ^oC. The air in the system is heated until the pressure reaches a pressure P2=750 kPa. The specific gas constant of the air is R=0.287 kJ/kg-K and the constant volume specific heat, cv-0.718 kJ/kg-K. 

The final temperature, T2, in K is

1,125.56

The total work done during the process described in Question, in kJ is 

0

Assuming that the specific heats are constant and that cv=0.718 kJ.kg-K, use the energy balance equation to calculate the heat transfer for the process, Q, described in Question 1 in kJ is

{Hint:  Compute the mass of air in the system first and use the energy balance equation to compute the heat transfer, Q]

11,008

Problem statement for Questions 8-10

A frictionless piston-cylinder device contains 5 kg of steam initially at P₁=500 kPa, T₁=200 ^oC. From the steam tables, at state 1, v₁=0.425 m³/kg and u₁=2643.3 kJ/kg.  Heat is transferred  isobarically until the final temperature T₂=300 ^oC. At state 2. From the steam tables, v₂=0.5226 m³/kg, u₂=2803.2 kJ/kg

With the values of v1 and v2 given for this isobaric process, compute the total work done in kJ  

244

Is the work done input energy or output energy

Output energy

Sketch your system on your test worksheet and show the energies going into the system, E_in, and all the energies going out of the system E_out, then use the energy balance equation E_in-E_out=U₂-U₁ to compute the heat transferred to the steam, Q,  in kJ.

1,044

Carbon dioxide, CO₂, with molecular weight, M=44.01 kg/kmol, is heated from T1=400 K to T2=900 K. Using Table A-20, the change in internal energy, u2-u1, in kJ/kg is 

451.625

Air is compressed in a piston-cylinder arrangement polytropically from an initial state where P₁=150 kPa and V₁=2.0 m3 and T₁=300 K , to a final state where P₂=1500 kPa. The polytropic index, n=1.6. 

 

The final volume. V2, in m3 is

0.4743

Calculate the work done by the compressor, W, in kJ ( if negative include the negative sign in your answer)

-685.75

The work done is an 

input work

If the computed mass of air in the system is 3.484 kg and the computed final temperature, T2=711.4 K,

Sketch your system on your test worksheet and show the energies going into the system, E_in, and all the energies going out of the system E_out, then use the energy balance equation E_in-E_out=U₂-U₁ to compute the heat transferred to the steam, Q,  in kJ. Assume ideal gas with constant specific heats and that cv-0.718 kJ/kg-K

343.6

The cp for a liquid is 4.18 kJ/kg-K. The cv for the liquid in kJ/kg-K is

4.18

The state of liquid water is changed from P1=350 kPa, T₁=20 ^oC to P₂=20 MPa  and T2=100 ^oC.

 

Determine the change in internal energy, Δu=u2-u1 of the water using the compressed liquid table and the approximation u=u_f@T when needed.

329.6

A liquid whose density is 900 kg/m³ is flowing in a pipe whose internal diameter is 0.05 m at a velocity of 10 m/s. What is the mass flow rate in kg/s?

17.67

A tank initially contained 700 kg of nitrogen.   The tank has 4 valves connected to it.  20 kg of nitrogen entered the tank though valve 1,  70 kg of nitrogen left the tank through valve 2,  125 kg of nitrogen entered the tank through valve 3,  and 200 kg of nitrogen left the tank through valve 4.  The final mass of nitrogen in the tank in kg is

575

Definition of specific enthalpy, Specific energy of a flowing fluid, Specific energy of a non-flowing fluid

h=u+Pv, 0=h+V2/2+gZ , e=u+V2/2 + gZ

The properties are the same everywhere in the system or control volume at a given time. The properties change from point to point inside the system or control volume at a given time.

Uniform State, Non-uniform state

The properties inside the system or control volume do not change with time at a given point. The properties change from time to time at a given point in the system or control volume.

Steady State, Unsteady State

Nozzles, Turbines, Compressors

Velocity V, Work output Wout, Work input, Win

Pumps, Heat Exchangers

Work input win, Heat Q

Steam steadily enters a nozzle at P1=5 MPa, T₁=500 ^oC  where h₁=3434.7  kJ/kg with a velocity of V₁=30 m/s. The steam exits the nozzle at P₂=1 MPa, T₂= 200 ^oC where h₂=2828.3 kJ/kg {Note that h values are in kJ/kfg and KE terms are in J/kg)

Applying the energy balance equation to the nozzle, the exit velocity, V₂, of the steam at the exit of the nozzle in m/s is

1,102

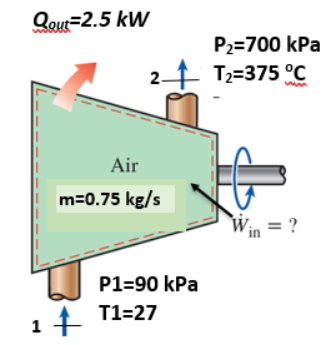
Problem Statement for Questions 9

For the air compressor shown in the figure, the air is an ideal gas with constant specific heats and that cp=1.005 kJ/kg-K and cv=0.718 kJ/kg-K.  The compressor loses heat at the rate  Q=2.5 kW as shown. The mass flow rate , m=0.75 kg/s.

By making an energy balance on the air compressor, the work input, Win, in kW is

264.8

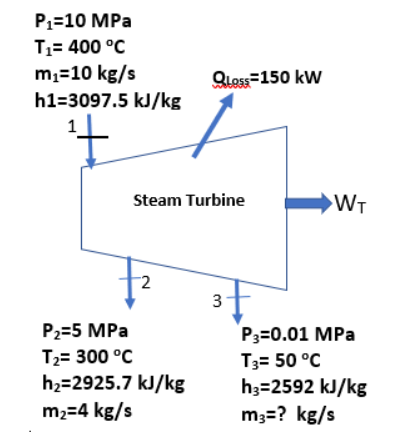
Problem statement for questions10 and 11.  (Assume Steady State Steady Flow and neglect all kinetic and potential energy changes)

For the turbine shown with all of the properties at the inlet state 1 and at the exit states 2 and 3 provided, make a mass balance to determine the mass flow rate, m3, at the exit state 3, in kg/s.

6

Make an energy balance on the turbine shown in Question 4 to determine the power output, W_T, in kW.

3,569.9

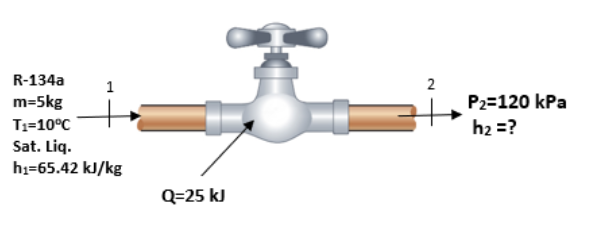
For the throttling valve shown, 5 kg of R-134a enters as a saturated liquid at 10 ^oC where the specific enthalpy is found to be h1=65.42 kJ/kg. The refrigerant gains 25 kJ of heat as it passes through the valve as shown. Apply the energy balance equation to find the specific enthalpy, h2, at the exit of the valve in kJ/kg.  Assume Steady State Steady Flow.

70.42