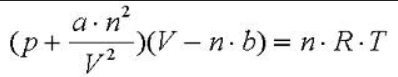Ch. 8 - Gases

Barometer

used to measure atmosphereic pressure

• P_atm = 760 mmHg

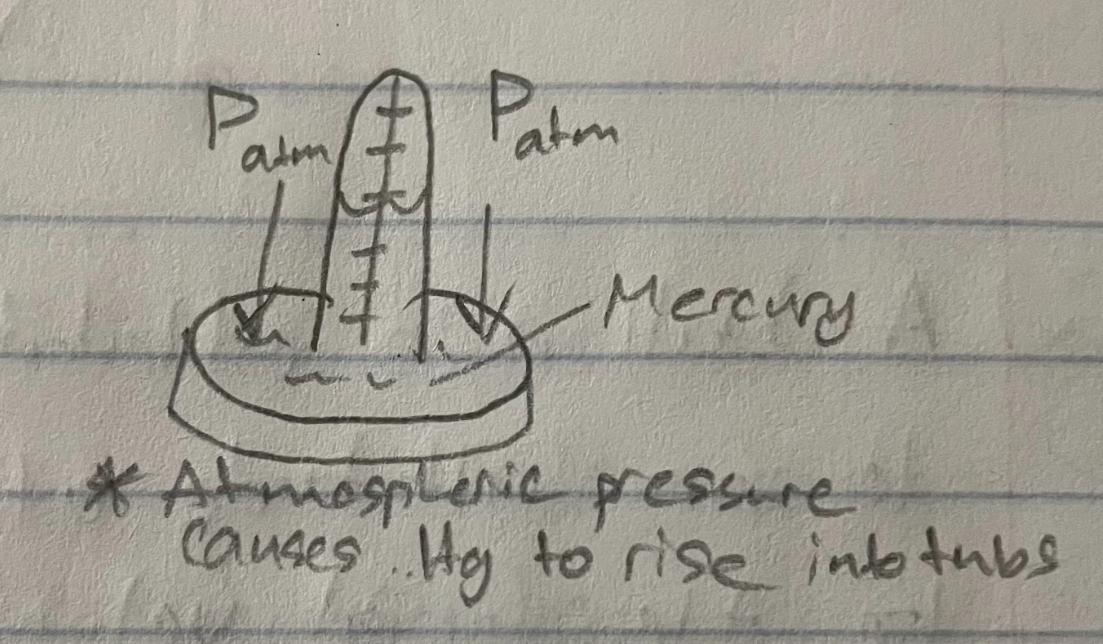
Manometer

used to measure pressure of a gas sample

closed end (manometer)

• pressure relative to a vacum

• Δheight = P_gas

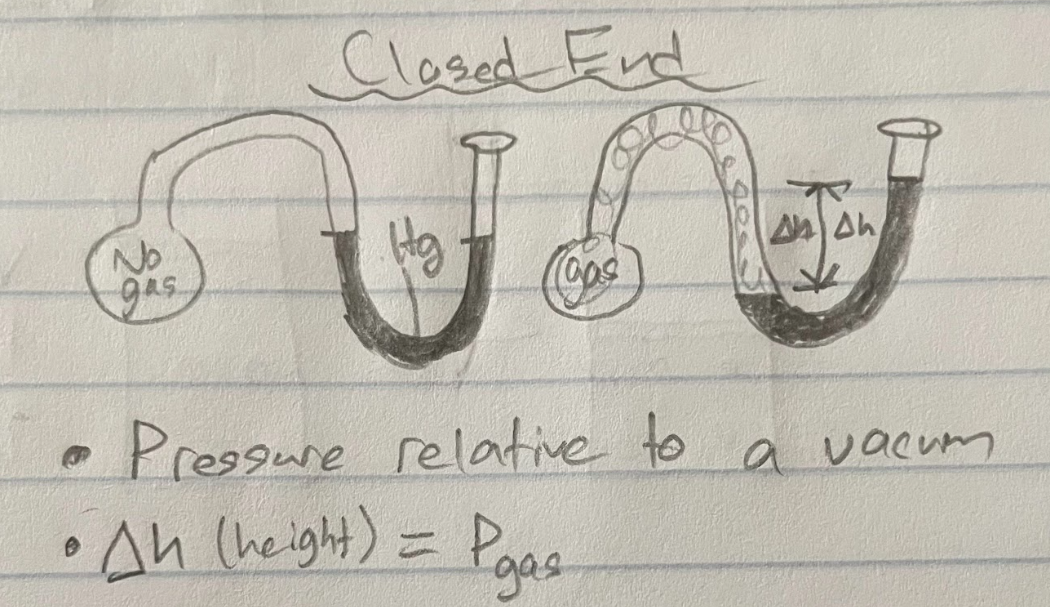
open end (manometer)

• Pressure relative to P_atm

• P_gas = P_atm ± Δheight

Pascal (Units of Pressure)

1 Pa = 1 N/m²

Atmosphere (Units of Pressure)

average atomospheric pressure

1 atm = 101.3 kPa = 1.013×10⁵ Pa = 1.013 bar

Boyle’s Law

P₁V₁ = P₂V₂

Charles’s Law

V₁ / T₁ = V₂ / T₂ (T in Kelvin)

Avogadro’s Law

V₁ / n₁ = V₂ / n₂

Ideal Gas Law

PV=nRT

R = 0.0821 L*atm/K*mol “universal gas constant”

P = usually in atm

STP

1 atm, 273 K

Density = m/V

n = m/MM

D = m/v = P*MM / R*T

Dalton’s Law in terms of pressure

P_tot = P_A + P_B + P_C…..

Dalton’s Law in terms of moles

P_tot = n_totRT / V

Dalton’s Law in terms of mole fraction

P_A = X_AP_tot P_A = (n_A/n_tot) * P_tot

Application of Dalton’s Law: Gas stoichiometry

1. Rxn that produces gas

2. Gas transported to the collector

3. Gas displaces water in the collector

   • Vapor pressure of water: water molecules escape surface and create a small partial pressure (Temp dependent)

The Postulates (KMT)

1.) Particle volume is assumed to be 0: gas particles are treated as “point masses”

2.) Gas particles are in constant, random motion collisions w/ the walls (causes pressure)

3.) The particles exert no forces on each other (not always true)

4.) The avg KE of the particles in proportional to Temp (K)

Pressure and Volume (KMT)

V decreases - P increases (Collisions increase (more frequent; NOT faster))

Pressure and Temp (KMT)

T increases - P increases (particles move faster and collisions are more frequent w/ more force)

Volume and Temp (KMT)

T increases - V increases (collisions more frequent and forceful)

Volume and Moles (KMT)

n increases - V increases (more gas particles; more collisions)

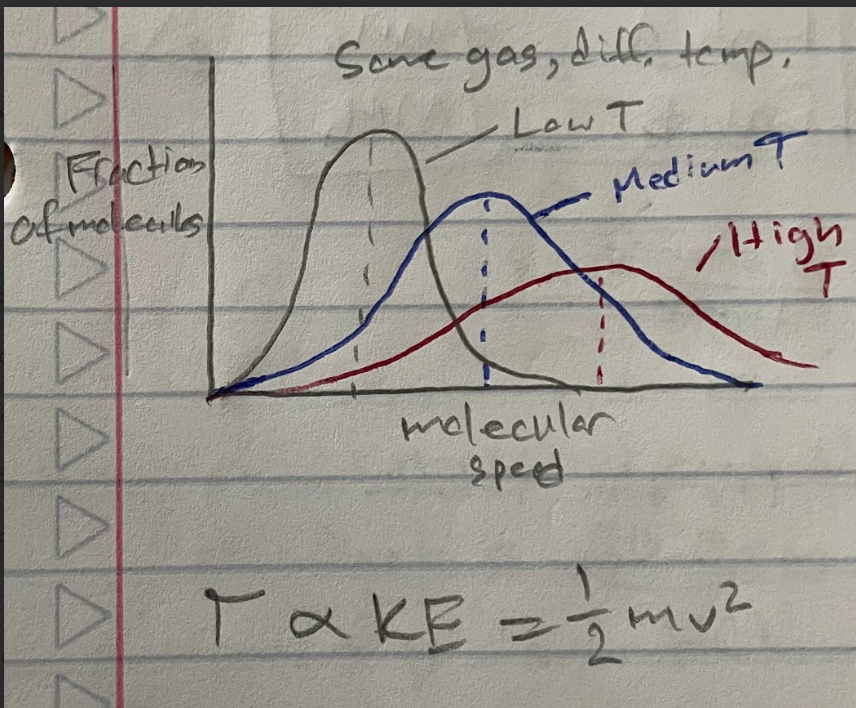
Same gas, different T

T and KE are proportional

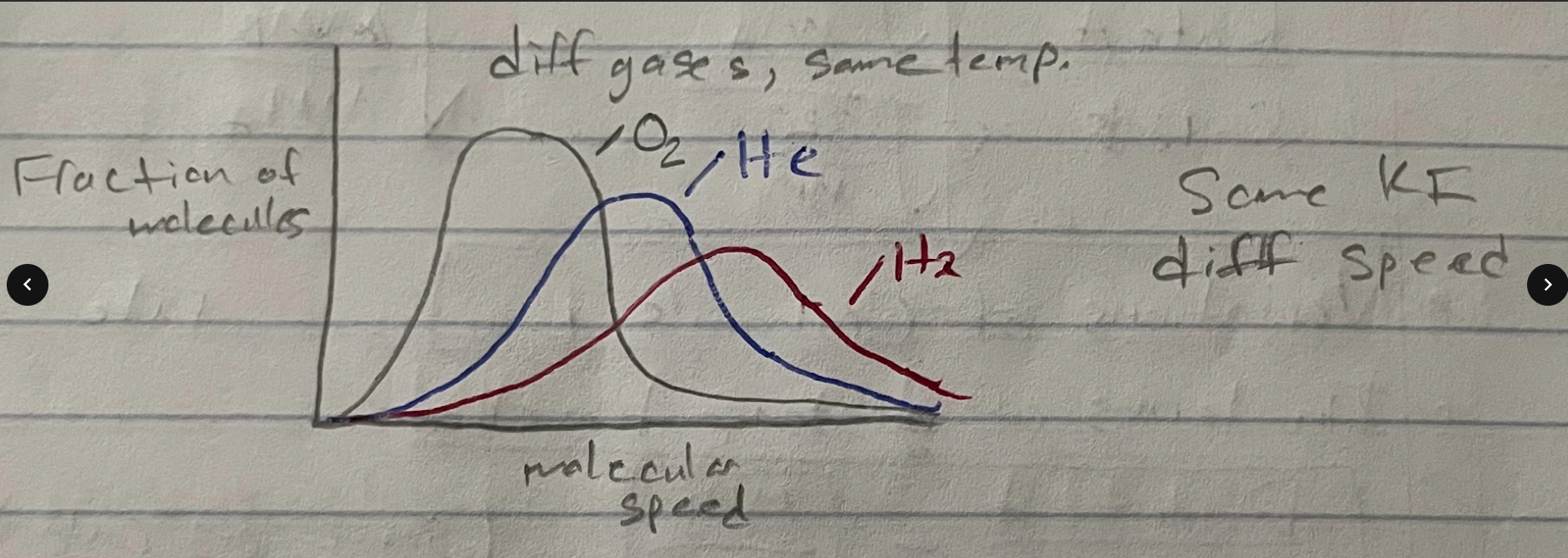
different gases, same T

• At a given T, the KE_avg will be constant, lighter gases will have higher avg speed

• The graph shows gases with same KE, different speeds

Equation relating molecular speed and temp (rms speed)

R = 8.314 J/K*mol

MM = in kg/mol

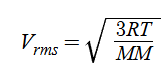
Grahams Law of Effusion/Diffusion

Effusion: escape of a gas from a small hole

Diffusion: movement of a gas through another gas

• Equations relates rates

• MM in g/mol

• rate in mL

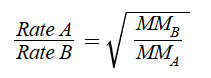
In terms of distance travelled

• same as rate

• no time mentioned

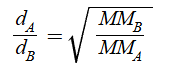
In terms of time

• MM_A and MM_B switch

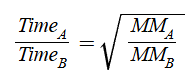
Real gases

deviations from ideal gas behavior

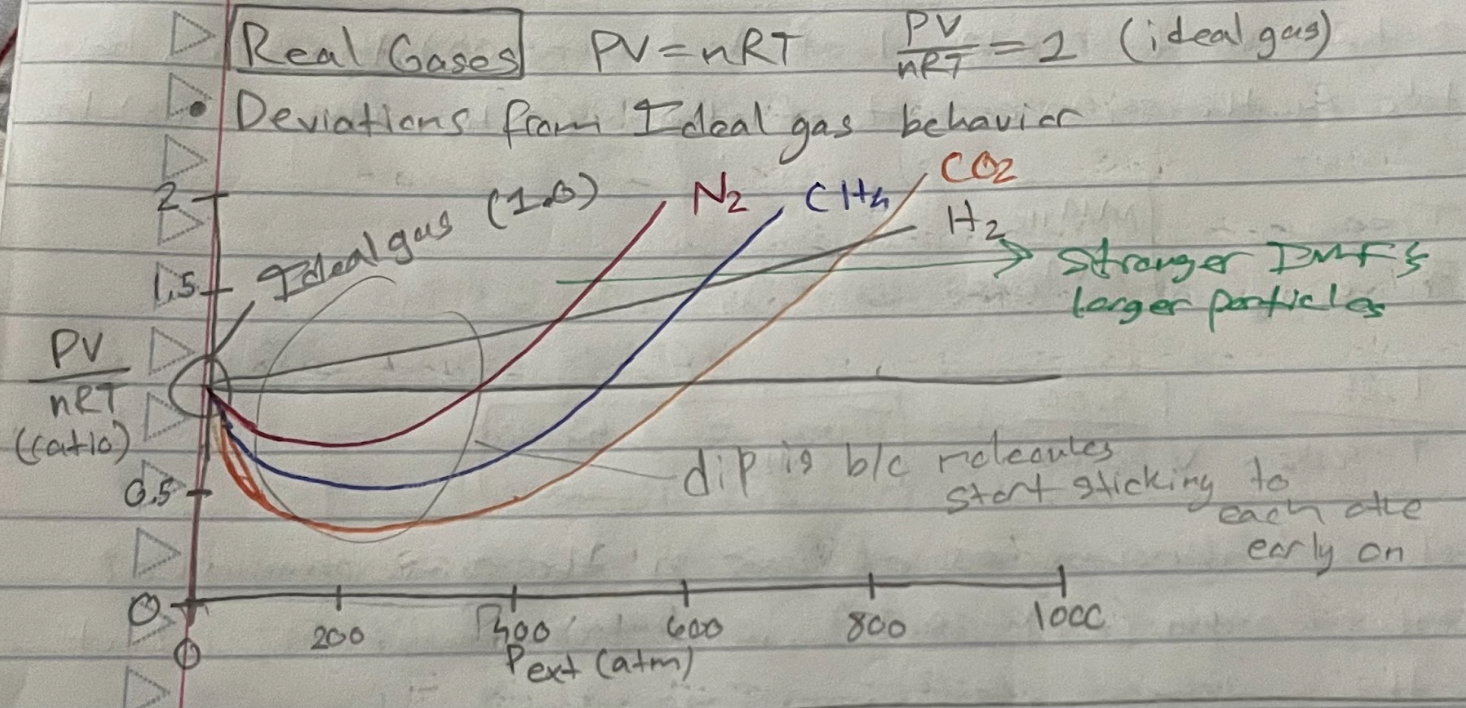
When do real gases behave most like ideal gases?

• Low P: Gas particles very far apart from each other

  • minimizes interactions

  • V_particles < < V_container

• High T: Gas particles moving very fast

  • Spend little time interacting with each other

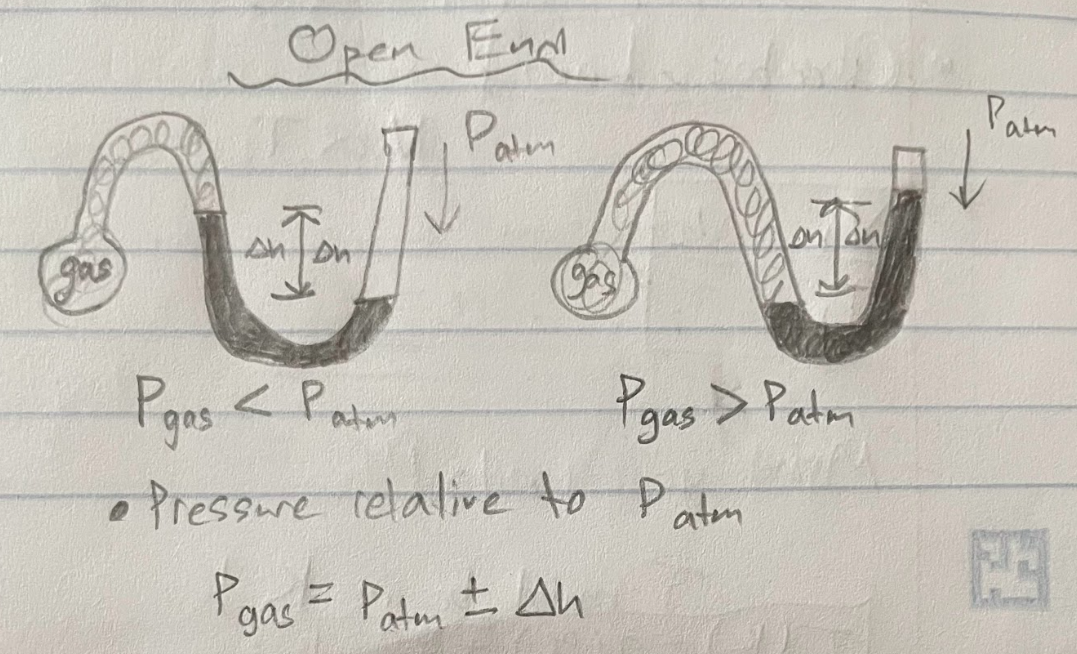
Van der Waals equation (for REAL gases)

• do not need to ever use, but understand the components

• a: adjusts for interparticle attractive forces (IMF increases; a increases)

• b: Adjusts V to account for particle volume (repulsive forces (volume); the size of particles increases, b increases)